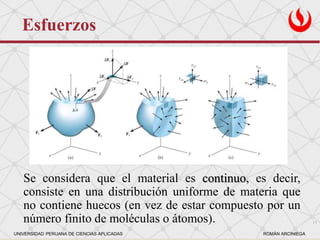
Este documento presenta conceptos fundamentales de esfuerzo y deformación en mecánica de materiales. Explica que la mecánica de materiales estudia el comportamiento de sólidos bajo cargas externas, determinando esfuerzos y deformaciones. Define esfuerzo como la fuerza interna por unidad de área y deformación como el cambio de forma bajo cargas. También cubre temas como esfuerzo normal, cortante, promedio, permisible y diseño, así como deformación normal y cortante unitaria.