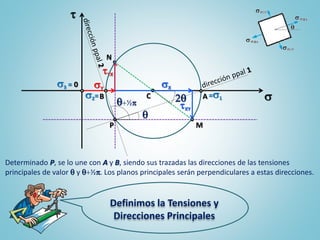
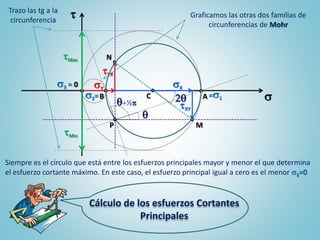
El documento describe la construcción y aplicación del círculo de Mohr para determinar las tensiones en un estado tensional plano en ingeniería mecánica y naval. Se detallan las fórmulas y gráficos necesarios para calcular las tensiones normales y tangenciales, así como las principales en un plano dado. Además, se menciona la clasificación de las tensiones en función de su dirección y se incluyen referencias bibliográficas relevantes.

1. Estados Planos de
Tensión
Circunferencia de Mohr
Curso de Estabilidad IIb
Ing. Gabriel Pujol
Para las carreas de Ingeniería Mecánica e Ingeniería Naval y Mecánica de la
Facultad de Ingeniería de la Universidad de Buenos Aires

2. Para el estado tensional dado en la figura es
de nuestro interés:
Construir la circunferencia de Mohr y
mediante ella determinar:
x
y
z
tXY
sX
sy
tYX
Las componentes de tensión en un plano que
forma un ángulo  con el eje x.
Las magnitudes y dirección de las
tensiones principales (s1 ; s2 ; s3)
Son datos del problema: sX ; sY ; sZ=0 ; tXY=tYX ; tXZ=tZX =tZY=tYZ =0;

3. Un estado tensional plano o bidimensional,
es aquel en el que uno de los planos está
libre de tensiones
La determinación de las tensiones puede
obtenerse utilizando un método gráfico. Las
ecuaciones del Estado Plano de Tensiones son:
que constituye la ecuación de una circunferencia de radio R y centro en un punto “C” de
coordenadas xC e yC = 0. Esta circunferencia se denomina Círculo de Mohr.
t
ss
t
t
ssss
s
2cos2sin
2
2sin2cos
22





 






xy
yx
xy
yxyx
elevando al cuadrado, sumando y
simplificando obtenemos:
2
2
2
2
22
xy
yxyx
t
ss
t
ss
s 




 





 

si llamamos
2
2
22
xy
yxyx
C Ryx t
ssss





 



y sustituimos en la ecuación anterior
obtenemos:
  222
RxC  ts
las coordenadas de cada punto de esta circunferencia representan las tensiones s y t
trazadas a cada uno de los infinitos planos que pasan por el punto.

4. Procedemos al trazado del círculo
de Mohr
Se considera positiva la tensión normal de tracción y negativa de compresión. La tensión
tangencial es positiva si el momento respecto del centro del elemento es en sentido horario.
t
s

5. Procedemos al trazado del círculo
de Mohr
Sobre un sistema de ejes coordenados s - t se ubican los puntos de coordenadas (sx;txy) y
(sy;tyx) estos puntos representan las tensiones normales y tangenciales que actúan sobre
las caras X e Y de un elemento.
t
s
sX
tXY
M
Defino el punto M
tYX
sY
N
Defino el punto N

6. Procedemos al trazado del círculo
de Mohr
Uniendo M con N donde corta al eje de abscisas tenemos el centro C. Con radio CM se traza
la circunferencia Mohr.
t
s
sX
tXY
M
tYX
sY
N
C
Círculo de Mohr
B A
Defino los puntos A y B

7. Definimos la Tensiones y
Direcciones Principales
Los puntos A y B donde la circunferencia intercepta al eje de abscisas determinan las
tensiones normales principales. La tercera tensión normal principal corresponde a s3=0
C
t
s
sX
tXY
M
tYX
sY
N
B As2= =s1
s3 = 0

8. Definimos la Tensiones y
Direcciones Principales
Trazando por M, de coordenadas (sX;tXY), una paralela al eje s y por N, de coordenadas
(sY;tYX), una paralela al eje t, defino el polo P del círculo de Mohr.
C
t
s
sX
tXY
M
tYX
sY
N
B As2= =s1
s3 = 0
// a s por M
// a t por N
P
Polo

9. Definimos la Tensiones y
Direcciones Principales
Determinado P, se lo une con A y B, siendo sus trazadas las direcciones de las tensiones
principales de valor  y ½p. Los planos principales serán perpendiculares a estas direcciones.
C
t
s
sX
tXY
M
tYX
sY
N
B As2= =s1
s3 = 0
P

2½p

10. Cálculo de las Tensiones respecto a
una dirección “” dada
Si dada la dirección (u) queremos conocer las tensiones según ella, trazamos por P una
paralela a u que corta a la circunferencia en D; la abscisa y ordenada de D nos dan s, y t .
C
t
s
sX
tXY
M
tYX
sY
N
B As2= =s1
s3 = 0
P

2½p
D
s
t


11. Cálculo de los esfuerzos Cortantes
Principales
Siempre es el círculo que está entre los esfuerzos principales mayor y menor el que determina
el esfuerzo cortante máximo. En este caso, el esfuerzo principal igual a cero es el menor s3=0
C
t
s
sX
tXY
M
tYX
sY
N
B As2= =s1
s3 = 0
P

2½p
Graficamos las otras dos familias de
circunferencias de Mohr
Trazo las tg a la
circunferencia
tMax
tMin

12. Bibliografía
Estabilidad II - E. Fliess
Introducción a la estática y resistencia de materiales - C. Raffo
Mecánica de materiales - F. Beer y otros
Resistencia de materiales - R. Abril / C. Benítez
Resistencia de materiales - Luis Delgado Lallemad / José M. Quintana Santana
Resistencia de materiales - V. Feodosiev
Resistencia de materiales - A. Pytel / F. Singer
Resistencia de materiales - S. Timoshenko

13. Muchas Gracias