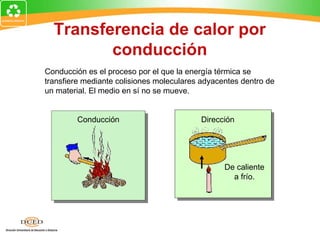
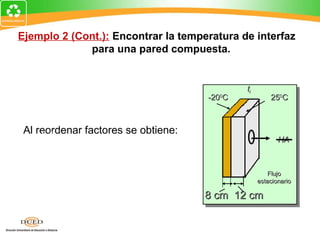
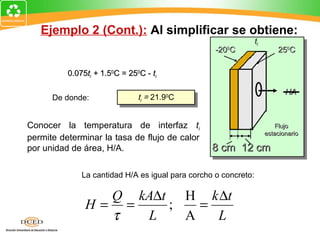
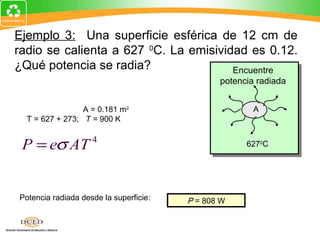
Aquí están los pasos para resolver este problema: 1. Dibuje un diagrama del proceso. 2. Identifique la información dada: mv = 4 g, tf = 600C 3. Identifique lo que se debe encontrar: mi 4. Escriba la ecuación de conservación de energía para el sistema: Qhielo = Qvapor 5. Resuelva la ecuación para encontrar mi La ecuación de conservación de energía es: mi(Lf + c∆T) = mvLv Donde: Lf = fusión del hielo c

1. CICLO 2012-III Módulo:I
Unidad: III Semana:5
FISICA II
Lic. Fis. Carlos Levano Huamaccto

2. CALOR
Fotografía © Vol.
05 Photodisk/Getty

3. CONTENIDO
-CALOR
-TEMPERATURA Y CANTIDAD DE CALOR
-CAPACIDAD CALORIFICA
-CAPACIDAD CALORIFICA ESPECÍFICA
-CONSERVACION DE ENERGÍA
-CAMBIO DE FASE

4. Calor definido como energía
El calor no es la energía que absorben o entregan entre los cuerpos o
El calor no es la energía que absorben o entregan entre los cuerpos o
sistemas.
sistemas.
La pérdida de calor por carbones calientes es igual a la que gana el
La pérdida de calor por carbones calientes es igual a la que gana el
agua.
agua.
Agua fría Equilibrio térmico
Carbones
calientes

5. Unidades de calor
Una caloría (1 cal) es la cantidad de calor que se requiere
para elevar la temperatura de 1 g de agua en 1 C0.
Ejemplo
10 calorías de calor elevarán la
temperatura de 10 g de agua en 10
C0.
Una kilocaloría (1 kcal) es la cantidad de calor que se
requiere para elevar la temperatura de 1 kg de agua en 1 C 0.

6. La unidad SI de calor
Dado que el calor es energía, el joule es la unidad preferida.
Entonces, la energía mecánica y el calor se miden en la misma
unidad fundamental.
Comparaciones de unidades de calor :
1 cal = 4.186 JJ
1 cal = 4.186 1 Btu = 778 ft lb
1 Btu = 778 ft lb
1 Btu = 252 cal
1 Btu = 252 cal
1 kcal = 4186 JJ
1 kcal = 4186
1 Btu = 1055 JJ
1 Btu = 1055

7. Temperatura y cantidad de calor
El efecto del calor sobre la temperatura
depende de la cantidad de materia 200C 220C
calentada.
A cada masa de agua en la figura se
aplica la misma cantidad de calor.
600 g
La masa más grande experimenta
un aumento más pequeño en 200C 300C
temperatura.
200 g

8. Capacidad Calorífica
La capacidad calorífica de una sustancia es el calor
que se requiere para elevar la temperatura un
grado.
Plomo Vidrio Al Cobre Hierro
1000C 1000C 1000C 1000C 1000C
37 s 52 s 60 s 83 s 90 s
Capacidades caloríficas con base en el tiempo para
calentar de cero a 1000C. ¿Cuál tiene la mayor
capacidad calorífica?

9. Capacidad calorífica (continúa)
Todas a 100 00Cse colocan en un bloque de parafina
Todas a 100 C se colocan en un bloque de parafina
Plomo Vidrio Al Cobre Hierro
Las bolas de hierro y cobre funden la parafina y salen
del otro lado; otras tienen capacidades caloríficas
menores.

10. Capacidad calorífica específica
La capacidad calorífica específica de un material es la cantidad de calor
La capacidad calorífica específica de un material es la cantidad de calor
necesario para elevar la temperatura de una unidad de masa en un grado.
necesario para elevar la temperatura de una unidad de masa en un grado.
Q
c= ; Q = mc∆t
m∆t
Agua: cc= 1.0 cal/g C00o 1 Btu/lb F00 o 4186 J/kg K
Agua: = 1.0 cal/g C o 1 Btu/lb F o 4186 J/kg K
Cobre: cc= 0.094 cal/g C00 o 390 J/kg K
Cobre: = 0.094 cal/g C o 390 J/kg K

11. Comparación de unidades de calor: ¿Cuánto calor se necesita
para elevar 1 kg de agua de 0 0C a 100 0C?
La masa de un kg de agua es:
1 kg = 1000 g = 0.454 lbm
Q = mc∆t 1 lbm = 454 g 1 kg
Para agua: c = 1.0 cal/g C0 o 1 Btu/lb
F0 o 4186 J/kg K

12. Ejemplo 1: Una taza de cobre 500 g se llena con 200 g
de café. ¿Cuánto calor se requirió para calentar taza y
café de 20 °C a 96 0C?
1. Dibuje bosquejo del problema.
2. Mencione información dada.
Masa taza mm = 0.500 kg
Masa café mc = 0.200 kg
Temperatura inicial de café y taza: t0 = 200C
Temperatura final de café y taza: tf = 960C
3. Mencione qué debe encontrar:
Calor total para elevar temperatura de café (agua) y taza a 960C.

13. Ejemplo 1(Cont.): ¿Cuánto calor se necesita para calentar taza y café de
20°C a 960C? mm = 0.2 kg; mw = 0.5 kg.
4. Recuerde fórmula o ley aplicable:
Ganancia o pérdida de calor: Q = mc ∆t
5. Decida qué calor TOTAL es el que se requiere
para elevar la temperatura de taza y agua (agua).
Escriba ecuación.
QT = mmcm ∆t + mwcw ∆t
6. Busque calores específicos en tablas:
Cobre: cm = 390 J/kg C0
Café (agua): cw = 4186 J/kg C0

14. Ejemplo 1(Cont.): ¿Cuánto calor se necesita para calentar taza y café
de 20°C a 960C?. mc = 0.2 kg; mw = 0.5 kg.
7. Sustituya info y resuelva el problema:
Cobre: cm = 390 J/kg C0
Café (agua): cw = 4186 J/kg C0
QT = mmcm ∆t + mwcw ∆t
Agua: (0.20 kg)(4186 J/kgC0)(76 C0)
Taza: (0.50 kg)(390 J/kgC0)(76 C0) ∆t = 960C --200C = 76 C00
∆t = 960C 200C = 76 C
QT = 63,600 J + 14,800 J
QT = 78.4 kJ
QT = 78.4 kJ

15. Una palabra acerca de las unidades
Las unidades sustituidas deben ser consistentes con las del valor
elegida de capacidad calorífica específica.
Por ejemplo: Agua cw = 4186 J/kg C0 o 1 cal/g C0
Q = mwcw ∆t
Si usa 1 cal/g C00para c, entonces Q debe
Si usa 1 cal/g C para c, entonces Q debe
estar en calorías yym en gramos.
estar en calorías m en gramos.
Las unidades para Q, m y ∆t deben ser
consistentes con las que se basen en el
valor de la constante c.
Si usa 4186 J/kg C00para c, entonces Q
Si usa 4186 J/kg C para c, entonces Q
debe estar en joules yym en kilogramos.
debe estar en joules m en kilogramos.

16. Conservación de energía
Siempre que haya transferencia de calor dentro de un sistema, la pérdida de
calor por los cuerpos más calientes debe ser igual al calor ganado por los
cuerpos más fríos:
Σ (pérdidas de calor) = Σ (calor ganado)
Σ (pérdidas de calor) = Σ (calor ganado)
Equilibrio térmico
Agua fría
Hierro
caliente

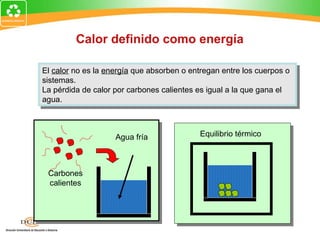
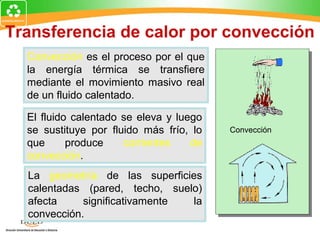
17. Ejemplo 2: Un puñado de perdigones
de cobre se calienta a 900C y luego se
sueltan en 80 g de agua en un vaso a
100C. Si la temperatura de equilibrio es
180C, ¿cuál fue la masa del cobre? te= 180C
cw = 4186 J/kg C0; cs = 390 J/kg C0
aislador
mw = 80 g; tw= 100C; ts = 900C a 900C
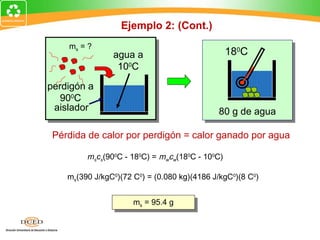
Pérdida de calor por perdigón = calor perdigón
ganado por agua 100C
mscs(900C - 180C) = mwcw(180C - 100C) agua a
Nota: las diferencias de temperatura son [alto - bajo] para asegurar valores
absolutos (+) perdido y ganado.

18. Ejemplo 2: (Cont.)
ms = ?
agua a 180C
100C
perdigón a
900C
aislador 80 g de agua
Pérdida de calor por perdigón = calor ganado por agua
mscs(900C - 180C) = mwcw(180C - 100C)
ms(390 J/kgC0)(72 C0) = (0.080 kg)(4186 J/kgC0)(8 C0)
2679 J m = 95.4 g
m = 95.4 g
ms = = 0.0954 kg
s
s
28,080 J/kg

19. Cambio de fase
Cuando ocurre un cambio de fase, sólo hay un cambio en energía
Cuando ocurre un cambio de fase, sólo hay un cambio en energía
potencial de las moléculas. La temperatura es constante durante el
potencial de las moléculas. La temperatura es constante durante el
cambio.
cambio.
Líquid Vaporización
Sólido o Gas
fusió
n
Q = mLf Q = mLv
Términos:
Términos: fusión, vaporización, condensación, calor latente,
fusión, vaporización, condensación, calor latente,
evaporación, punto de congelación, punto de fusión.
evaporación, punto de congelación, punto de fusión.

20. Cambio de Fase
El calor latente de fusión (Lf) de una sustancia
Q
es el calor por unidad de masa que se Lf =
requiere para cambiar la sustancia de la fase m
sólida a la líquida de su temperatura de
fusión. Para agua: L = 80 cal/g = 333,000 J/kg
Para agua: Lf = 80 cal/g = 333,000 J/kg
f
El calor latente de vaporización (Lv) de una
sustancia es el calor por unidad de masa que Q
se requiere para cambiar la sustancia de Lv =
líquido a vapor a su temperatura de ebullición. m
Para agua: Lv = 540 cal/g = 2,256,000 J/kg
Para agua: Lv = 540 cal/g = 2,256,000 J/kg

21. Fundido de un cubo de cobre
El calor Q que se requiere para fundir una sustancia a su temperatura
de fusión se puede encontrar si se conocen la masa y calor latente de
fusión.
Q = mLv
Q = mLv
¿Qué Q
Ejemplo: Para fundir por completo 2 kg de 2 kg
para
cobre a 10400C, se necesita: fundir
Q = mLf = (2 kg)(134,000 J/kg) cobre?
Lf = 134 kJ/kg
Q = 268 kJ
Q = 268 kJ

22. Ejemplo 3: ¿Cuánto calor se necesita para convertir 10 g de hielo a
-200C a 1000C?
Primero, revise gráficamente el proceso como se muestra:
temperatura t
hielo vapor 540 cal/g
1000
C
1 cal/gC0 sólo
vapor
vapor y
80 cal/g agua
00C
sólo agua
hielo y agua
-20 C
0 hiel chielo= 0.5 cal/gC0 Q
o

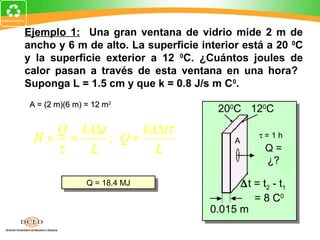
23. Ejemplo 3 (Cont.): El paso uno es Q1 para convertir 10 g de hielo a
-200C a hielo a 00C (no agua todavía).
Q1 para elevar hielo a 00C: Q1 = mc∆t
-200C 00C
t
1000 Q1 = (10 g)(0.5 cal/gC0)[0 - (-200C)]
C
Q1 = (10 g)(0.5 cal/gC0)(20 C0)
Q1 = 100 cal
Q1 = 100 cal
00C
chielo= 0.5 cal/gC0
-200C hiel
Q
o

24. Ejemplo 3 (Cont.): El paso dos es Q2 para
convertir 10 g de hielo a 00C a agua a 00C.
Q2 para fundir 10 g de hielo a 00C: Q2 =
fusión
mLf
t
1000 Q2 = (10 g)(80 cal/g) = 800 cal
C
Q2 = 800 cal
Q2 = 800 cal
80 cal/g Sume esto a Q1 = 100 cal: 900 cal usadas
00C hasta este punto.
hielo y agua
-20 C
0
Q

25. Ejemplo 3 (Cont.): El paso tres es Q3 para cambiar 10 g de agua a
00C a agua a 1000C.
Q3 para elevar agua a 00C a 1000C.
00C to 1000C Q3 = mc∆t ; cw= 1 cal/gC0
t
Q3 = (10 g)(1 cal/gC0)(1000C - 00C)
1000
C Q3 = 1000 cal
Q3 = 1000 cal
1 cal/gC0
Total = Q1 + Q2 + Q3 = 100
00C +900 + 1000 = 1900 cal
sólo agua
-200C Q

26. Ejemplo 3 (Cont.): El paso cuatro es Q4 para convertir 10 g de
agua a vapor a 1000C? (Q4 = mLv)
Q4 para convertir toda el agua a 1000C
vaporización a vapor a 1000C. (Q = mLv)
Q4 = (10 g)(540 cal/g) = 5400 cal
1000
C
5400 cal Calor total:
800 cal
100 cal 1000 cal 7300 cal
7300 cal
00C vapor y
hielo y sólo agua
-200C hielo agua agua Q

27. Ejemplo 4: ¿Cuántos gramos de hielo a 00C se deben mezclar con
cuatro gramos de vapor para producir agua a 600C?
mi = ?
Hielo: fundir y luego elevar a 600C. Vapor: condensar y
caer a 600C. hiel
o
vapor
Calor total ganado = Pérdida de calor total 4g
miLf + micw∆t = msLv + mscw∆t te = 600C
Nota: Todas las pérdidas y ganancias son valores absolutos
(positivos).
Total ganado: mi(80 cal/g) + mi(1 cal/gC0)(60 C0 - 00C )
Pérdida: (4 g)(540 cal/g) + (4 g)(1 cal/gC0)(100 C0 - 600C )

28. Ejemplo 4 (continuación)
Total ganado: mi(80 cal/g) + mi(1 cal/gC0)(60 C0)
mi = ?
Total perdido: (4 g)(540 cal/g) + (4 g)(1 cal/gC 0)(40 C0)
4g
Calor total ganado = calor total perdido
80mi + 60mi = 2160 g +160 g te = 600C
2320 g
mi = mi = 16.6 g
mi = 16.6 g
140

29. hiel agua
o
Ejemplo 5: Cincuenta gramos de hielo se
mezclan con 200 g de agua inicialmente a 70 0C.
Encuentre la temperatura de equilibrio de la 00C 700C
mezcla. 50 g 200 g
Hielo: funde y eleva a te Agua: cae de 70 a te. te = ?
Calor ganado: miLf + micw∆t ; ∆t = te - 00C
Ganancia = (50 g)(80 cal/g) + (50 g)(1 cal/gC0)(te - 00C )
Ganancia = 4000 cal + (50 cal/g)te

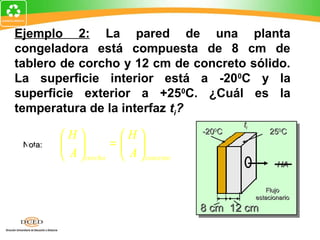
30. Ejemplo 5 (Cont.):
Ganancia = 4000 cal + (50 cal/g)te
Pérdida de calor = mwcw∆t 00C 700C
∆t = 700C - te [alto - bajo] 50 g 200 g
te = ?
Pérdida = (200 g)(1 cal/gC0)(700C- te )
Pérdida = 14,000 cal - (200 cal/C0) te
El calor ganado debe ser igual al calor perdido:
4000 cal + (50 cal/g)te = 14,000 cal - (200 cal/C0) te

31. Ejemplo 5 (Cont.):
El calor ganado debe ser igual al calor perdido:
4000 cal + (50 cal/g)te = 14,000 cal - (200 cal/C0) te
Al simplificar se tiene: (250 cal/C0) te = 10,000 cal
10,000 cal
te = 0
= 40 C
0
250 cal/C 00C
50 g
700C
200 g
ttee = 4000C
= 40 C te = ?

32. Transferencia de calor

33. CONTENIDO
• TRANSFERENCIA DE CALOR POR
CONDUCCIÓN
• TRANSFERENCIA DE CALOR POR CONVECCIÓN
• TRANSFERENCIA DE CALOR POR RADIACIÓN

34. Transferencia de calor por
conducción
Conducción es el proceso por el que la energía térmica se
transfiere mediante colisiones moleculares adyacentes dentro de
un material. El medio en sí no se mueve.
Conducción Dirección
De caliente
a frío.

35. Transferencia de calor por convección
Convección es el proceso por el que
la energía térmica se transfiere
mediante el movimiento masivo real
de un fluido calentado.
El fluido calentado se eleva y luego
se sustituye por fluido más frío, lo Convección
que produce corrientes de
convección.
La geometría de las superficies
calentadas (pared, techo, suelo)
afecta significativamente la
convección.

36. Transferencia de calor por radiación
Radiación es el proceso por el
que la energía térmica se
transfiere mediante ondas
electromagnéticas.
Radiación
Sol

37. Corriente calorífica
La corriente calorífica H se define como la cantidad de calor Q
transferida por unidad de tiempo τ en la dirección de mayor temperatura
a menor temperatura.
vapor hiel
o
Q
H= ( J / s)
τ
Unidades típicas son: J/s, cal/s y Btu/h

38. Conductividad térmica
La conductividad térmica k de un
t1 t2
material es una medida de su
habilidad para conducir calor.
∆t = t2 - t1
Q kA∆t QL
H= = k= J
τ L
Aτ ∆t
Unidades =
s ⋅ m ⋅ C°

39. Las unidades SI para conductividad
Calient Frío QL
e k=
Aτ ∆t
Para cobre: kk= 385 J/s m C00
Para cobre: = 385 J/s m C
En unidades SI, por lo general mediciones pequeñas de longitud L y
En unidades SI, por lo general mediciones pequeñas de longitud L y
área A se deben convertir a metros yy metros cuadrados,
área A se deben convertir a metros metros cuadrados,
respectivamente, antes de sustituir en fórmulas.
respectivamente, antes de sustituir en fórmulas.

40. Unidades antiguas de
conductividad
∆t = 1 F0
Unidades antiguas, todavía activas, usan
τ=1h mediciones comunes para área en ft2,
A=1 ft2 tiempo en horas, longitud en pulgadas y
cantidad de calor en Btu.
Q=1 Btu
L = 1 in. k de vidrio = 5.6 Btu in/ft2h F0
Tomado literalmente, esto significa que, para una placa de vidrio
de 1 in de espesor, cuya área es 1 ft2 y cuyos lados difieren en
temperatura por 1 F0, el calor se conducirá a la tasa de 5.6 Btu/h.

41. Conductividades térmicas
A continuación se dan ejemplos de los dos sistemas de
unidades para conductividades térmicas de materiales:
Material J/s ⋅ m ⋅ C o
Btu ⋅ in/ft 2 ⋅ h ⋅ F0
Cobre: 385 2660
Concreto o vidrio: 0.800 5.6
0.040 0.30
Tablero de corcho:

42. Ejemplos de conductividad térmica
Comparación de corrientes caloríficas para condiciones
similares: L = 1 cm (0.39 in); A = 1 m 2 (10.8 ft2); ∆t = 100 C0
2050 kJ/s 4980 Btu/h
Aluminio:
3850 kJ/s 9360 Btu/h
Cobre:
Concreto o vidrio: 8.00 kJ/s 19.4 Btu/h
Tablero de corcho: 0.400 kJ/s 9.72 Btu/h

43. Ejemplo 1: Una gran ventana de vidrio mide 2 m de
ancho y 6 m de alto. La superficie interior está a 20 0C
y la superficie exterior a 12 0C. ¿Cuántos joules de
calor pasan a través de esta ventana en una hora?
Suponga L = 1.5 cm y que k = 0.8 J/s m C0.
A = (2 m)(6 m) = 12 m2
200C 120C
Q kA∆ t kA∆ tτ
H= = ; Q= A
τ=1h
τ L L Q=
¿?
Q = 18.4 MJ
Q = 18.4 MJ ∆t = t2 - t1
= 8 C0
0.015 m

44. Ejemplo 2: La pared de una planta
congeladora está compuesta de 8 cm de
tablero de corcho y 12 cm de concreto sólido.
La superficie interior está a -200C y la
superficie exterior a +250C. ¿Cuál es la
temperatura de la interfaz ti?
ti
H H -20 C 250C
0
k1 ti − (−200   =k A  0 C - ti 
Nota:
  A  corcho   25concreto 
C)  2 
= HA
L1 0 L
k1 (ti + 20 C) k2 (25 C - ti )
0 2
= Flujo
L1 L2 estacionario
8 cm 12 cm

45. Ejemplo 2 (Cont.): Encontrar la temperatura de interfaz
para una pared compuesta.
k1 (ti + 200 C) k2 (250 C - ti )
= ti
L1 L2 -20 C
0
250C
Al reordenar factores se obtiene:
k1L 2 HA
(ti + 200 C) = (250 C - ti )
k2 L1
k1L 2 (0.04 W/m ⋅ C0 )(0.12 m)
= = 0.075 Flujo
k2 L1 (0.8 W/m ⋅ C )(0.08 m)
0 estacionario
8 cm 12 cm

46. Ejemplo 2 (Cont.): Al simplificar se obtiene:
ti
(0.075)(ti + 20 C) = (25 C - ti )
0 0 -200C 250C
0.075ti + 1.50C = 250C - ti
HA
De donde: tit = 21.90C
= 21.90C
i
Conocer la temperatura de interfaz ti Flujo
estacionario
permite determinar la tasa de flujo de calor
por unidad de área, H/A. 8 cm 12 cm
La cantidad H/A es igual para corcho o concreto:
Q kA∆t H k ∆t
H= = ; =
τ L A L

47. Ejemplo 2 (Cont.): Flujo estacionario constante.
H/A es constante en el tiempo, de modo ti
-20 C
0
250C
que diferentes k producen diferentes ∆t
Corcho: ∆t = 21.90C - (-200C) = 41.9 C0
HA
Concreto: ∆t = 250C - 21.90C = 3.1 C0
Flujo
Q kA∆t H k ∆t estacionario
H= = ; = 8 cm 12 cm
τ L A L
Dado que H/A es el mismo, elija sólo concreto:
H
H k ∆t
= =
(0.8 W/mC 0 )(3.1 C 0 ) = 20.7 W/m 2
A L 0.12 m A

48. Ejemplo 2 (Cont.): Flujo estacionario constante.
t i
-200C 250C
H
= 20.7 W/m 2
HA
A
Corcho: ∆t = 21.90C - (-200C) = 41.9 C0 Flujo
estacionario
Concreto: ∆t = 250C - 21.90C = 3.1 C0 8 cm 12 cm
Note que 20.7 Joules de calor por segundo pasan
a través de la pared compuesta. Sin embargo, el
intervalo de temperatura entre las caras del corcho Si A = 10 m2, ,el flujo de
Si A = 10 m2 el flujo de
es 13.5 veces más grande que para las caras del calor en 1 h sería ______
calor en 1 h sería ______
concreto.
745 kW

49. Radiación
La tasa de radiación R es la energía emitida por unidad de área por
unidad de tiempo (potencia por unidad de área).
Q P P
Tasa de radiación (W/m ):
2
R= = R = = eσ T 4
τA A A
Emisividad, e : :
Emisividad, e 0>e >1
0>e >1
Constante de Stefan-Boltzman:
Constante de Stefan-Boltzman: σ = 5.67 xx
σ = 5.67
10-8-8W/m·K44
10 W/m·K

50. Ejemplo 3: Una superficie esférica de 12 cm de
radio se calienta a 627 0C. La emisividad es 0.12.
¿Qué potencia se radia? Encuentre
potencia radiada
A = 4π R = 4π (0.12 m)
2 2
A = 0.181 m2 A
T = 627 + 273; T = 900 K
P = eσ AT 4 6270C
P = (0.12)(5.67 x 10 W/mK )(0.181 m )(900 K)
-8 4 2 4
Potencia radiada desde la superficie: P = 808 W
P = 808 W

51. GRACIAS