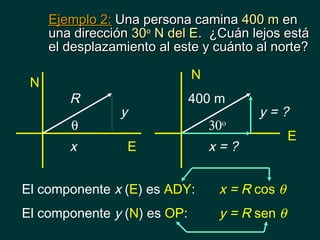
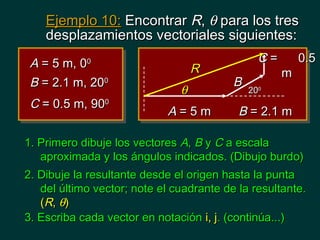
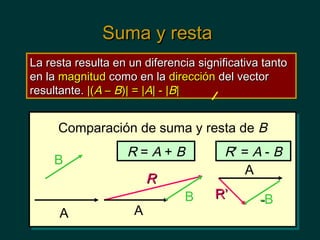
El documento presenta conceptos básicos de bioestadística y vectores. Introduce la medición de longitud y desplazamiento, explicando que la longitud es una cantidad escalar mientras que el desplazamiento es una cantidad vectorial que contiene magnitud y dirección. También explica cómo identificar direcciones usando referencias al este, norte, oeste y sur, y cómo representar vectores usando coordenadas polares y rectangulares. Finalmente, muestra ejemplos de cómo calcular componentes de vectores y la fuerza resultante de vectores perpendiculares.

1. UNIVERSIDAD ARZOBISPO LOAYZA
SEMANA2: BIOESTATICA
VECTORES
LIC. FIS. CARLOS LEVANO

2. La física es la ciencia
de la medición
Longitud Peso Tiemp
o
Comience con la medición de longitud:
Comience con la medición de longitud:
su magnitud y su dirección.
su magnitud y su dirección.

3. Distancia: cantidad escalar
 Distancia es la longitud de la ruta
 Distancia es la longitud de la ruta
tomada por un objeto.
tomada por un objeto.
Una cantidad escalar:
s = 20 m B
Sólo contiene magnitud
y consiste de un
A
número y una unidad.
(20 m, 40 mi/h, 10 gal)

4. Desplazamiento-Cantidad vectorial
•• Desplazamiento es la separación en
Desplazamiento es la separación en
línea recta de dos puntos en una
línea recta de dos puntos en una
dirección especificada.
dirección especificada.
Una cantidad vectorial:
D = 12 m, 20o B
Contiene magnitud Y
A dirección, un número,
θ unidad y ángulo.
(12 m, 300; 8 km/h, N)

5. Distancia y desplazamiento
•• Desplazamiento es la coordenada x o y
Desplazamiento es la coordenada x o y
de la posición. Considere un auto que
de la posición. Considere un auto que
viaja 4 m E, luego 6 m W.
viaja 4 m E, luego 6 m W.
Desplazamiento neto:
D 4 m, E D = 2 m, W
¿Cuál es la distancia
x = -2 x = +4 recorrida?
6 m, W ¡¡ 10 m !!

6. Identificación de dirección
Una forma común de identificar la dirección
Una forma común de identificar la dirección
es con referencia al este, norte, oeste y sur.
es con referencia al este, norte, oeste y sur.
(Ubique los puntos
(Ubique los puntos abajo.)
abajo.)
N Longitud = 40 m
40 m, 50o N del E
60o 50o
W E 40 m, 60o N del W
60o
60o
40 m, 60o W del S
40 m, 60o S del E
S

7. Identificación de dirección
Escriba los ángulos que se muestran a continuación
Escriba los ángulos que se muestran a continuación
con referencias al este, sur, oeste, norte.
con referencias al este, sur, oeste, norte.
N N
45o
W E
50o W E
S
S
5000 S del E
50 S del E 4500 W del N
45 W del N
Clic para ver las respuestas...
Clic para ver las respuestas...

8. Vectores y coordenadas polares
Las coordenadas polares R, θ son una
Las coordenadas polares ((R, θ)) son una
excelente forma de expresar vectores. Considere,
excelente forma de expresar vectores. Considere,
por ejemplo, al vector 40 m, 5000N del E..
por ejemplo, al vector 40 m, 50 N del E
90o 90o
40 m R
180o 50o 180o θ
0o 0o
270o 270o
R es la magnitud y θ la dirección.

9. Vectores y coordenadas polares
Se dan coordenadas polares ((R,, θ)) para
Se dan coordenadas polares R θ para
cada uno de los cuatro posibles cuadrantes:
cada uno de los cuatro posibles cuadrantes:
90o
(R, θ) = 40 m, 50o
120 o
210o
60 o
50 o (R, θ) = 40 m, 120o
180
o
0o
60o
60o (R, θ) = 40 m, 210o
3000
(R, θ) = 40 m, 300o
270o

10. Coordenadas rectangulares
y La referencia se
(-2, +3) hace a los ejes x y
(+3, +2) y, y los números
+ + y – indican
+ posición en el
x
- espacio.
Derecha, arriba = (+, +)
- Izquierda, abajo = (-, -)
(x, y) = (?, ?)
(-1, -3) (+4, -3)

11. Repaso de trigonometría
• Aplicación de trigonometría a vectores
Trigonometría y
sen θ = y = R sen θ
y = R sen θ
R
y R x
cos θ = x = R cos θ
x = R cos θ
R
θ y
x tan θ = R22 = x22 + y22
R =x +y
x

12. Cómo encontrar componentes
de vectores
Un componente es el efecto de un vector a lo
largo de otras direcciones. A continuación se
ilustran los componentes x y y del vector (R, θ).
x = R cos θ
R y = R sen θ
y
θ
x Cómo encontrar componentes:
Conversiones de polar a

13. Ejemplo 2: Una persona camina 400 m en
una dirección 30o N del E. ¿Cuán lejos está
el desplazamiento al este y cuánto al norte?
N
N
R 400 m
y y=?
θ 30ο
E
x E x=?
El componente x (E) es ADY: x = R cos θ
El componente y (N) es OP: y = R sen θ

14. Ejemplo 2 (cont.): Una caminata de 400 m en
una dirección a 30o N del E. ¿Cuán lejos está
el desplazamiento del este y cuánto del norte?
N Nota: x es el lado
400 m adyacente al ángulo de 300
y=?
30ο
E ADY = HIP x cos 300
x=?
x = R cos θ
x = (400 m) cos 30o El componente x es:
= +346 m, E Rx = +346 m

15. Ejemplo 2 (cont.): Una caminata de 400 m en
una dirección a 30o N del E. ¿Cuán lejos está
el desplazamiento del este y cuánto del norte?
N Nota: y es el lado opuesto
400 m al ángulo de 300
y=?
30ο
E OP = HIP x sen 300
x=?
y = R sen θ
y = (400 m) sen 30o El componente y es:
= + 200 m, N Ry = +200 m

16. Ejemplo 2 (cont.): Una caminata de 400 m en
una dirección a 30o N del E. ¿Cuán lejos está
el desplazamiento del este y cuánto del norte?
N
400 m Los
Ry = +200 componentes x y
30ο m y son cada uno
E + en el primer
Rx =
cuadrante
+346 m
Solución: La persona se desplaza 346 m al
este y 200 m al norte de la posición original.

17. Signos para coordenadas
rectangulares
90o
Primer cuadrante:
R es positivo (+)
R + 0o > θ < 90o
θ
0o x = +; y = +
+
x = R cos θ
y = R sen θ

18. Signos para coordenadas
rectangulares
90o
Segundo
cuadrante:
R
R es positivo (+)
+ θ
180o 90o > θ < 180o
x=-; y=+
x = R cos θ
y = R sen θ

19. Signos para coordenadas
rectangulares
Tercer cuadrante:
R es positivo (+)
θ 180o > θ < 270o
180o
x=- y=-
-
R x = R cos θ
y = R sen θ
270o

20. Signos para coordenadas
rectangulares
Cuarto cuadrante:
R es positivo (+)
θ 270o > θ < 360o
+ 360o
x=+ y=-
R x = R cos θ
y = R sen θ
270 o

21. Resultante de vectores
perpendiculares
Encontrar la resultante de dos vectores perpendiculares
es como cambiar de coordenadas rectangulares a
polares.
R R= x +y 2 2
y
θ
y
x tan θ =
x
R siempre es positivo; θ es desde el eje +x

22. Ejemplo 3: Una fuerza de 30 lb hacia el sur y
una de 40 lb hacia el este actúan sobre un
burro al mismo tiempo. ¿Cuál es la fuerza
NETA o resultante sobre el burro?
Dibuje un esquema burdo. Elija una escala burda:
Ej: 1 cm = 10 lb
40 lb 40 lb
Nota: La fuerza tiene direccióncm = 40 lbla
Nota: La fuerza tiene dirección tal como la
4 tal como
longitud. Los vectores fuerza se pueden tratar
longitud. Los vectores fuerza se pueden tratar
30 lb
como si se tuvieran vectores3longitud para
cm = 30 lb
longitud para
como si se tuvieran vectores
30 lb
encontrar la fuerza resultante. ¡El
encontrar la fuerza resultante. ¡El

23. Cómo encontrar la resultante (cont.)
Encontrar (R, θ) a partir de (x, y) dados = (+40, -30)
40 lb θ Rx 40 lb
φ
Ry
30 lb R 30 lb
R= x2 + y2 R= (40)2 + (30)2 = 50 lb
-30
tan φ = φ = -36.9o θ = 323.1oo
θ = 323.1
40

24. Cuatro cuadrantes (cont.)
30 lb
R R 30 lb
R = 50 lb
Ry Ry
θ
φ θ
Rx Rx 40 lb
40 lb
40 lb Rx θ θ Rx 40 lb
φ φ
Ry Ry
R = 50 lb
30 lb R R 30 lb
φ = 36.9oo;; θ = 36.9oo;; 143.1oo;; 216.9oo;; 323.1oo
φ = 36.9 θ = 36.9 143.1 216.9 323.1

25. Notación vector unitario (i, j, k)
y Considere ejes 3D (x, y, z)
j Defina vectores unitarios i, j, k
i x
k Ejemplos de uso:
z 40 m, E = 40 i 40 m, W = -40 i
30 m, N = 30 j 30 m, S = -30 j
20 m, out = 20 k 20 m, in = -20 k

26. Ejemplo 4: Una mujer camina 30 m, W;
luego 40 m, N. Escriba su desplazamiento
en notación i, j y en notación R, θ.
En notación i, j se tiene:
+40 m R R = R x i + Ry j
φ Rx = - 30 m Ry = + 40 m
-30 m
R = -30 ii + 40 jj
R = -30 + 40
El desplazamiento es 30 m oeste
El desplazamiento es 30 m oeste y
y
40 m norte de la posición de partida.
40 m norte de la posición de partida.

27. Ejemplo 4 (cont.): A continuación se
encuentra su desplazamiento en
notación R, θ.
+ 40
tan φ = ; φ = 59.10
+40 R − 30
m
φ θ = 1800 – 59.10
-30 m
θ = 126.9oo
θ = 126.9
R = (−30) + (40)
2 2
R = 50 m
R = 50 m
((R,, θ)) = (50 m, 126.9oo))
R θ = (50 m, 126.9

28. Ejemplo 6: La ciudad A está 35 km al sur y
46 km al oeste de la ciudad B. Encuentre la
longitud y dirección de la autopista entre las
ciudades.
46 km
R = -46 i – 35 j
φ=?
R = (46 km) 2 + (35 km) 2 35 B
km
R = 57.8 km R=?
R = 57.8 km
A
−46 km
tan φ =
−35 km θ = 1800 + 52.70
φ = 52.700 S de W.
φ = 52.7 S de W. θ = 232.700
θ = 232.7

29. Ejemplo 7. Encuentre los componentes de la
fuerza de 240 N que ejerce el niño sobre la niña
si su brazo forma un ángulo de 280 con el suelo.
F = 240 N
Fy F
280
Fy
Fx
Fx = -|(240 N) cos 280| = -212 N O en notación i, j :
Fy = +|(240 N) sen 280| = +113 N F = -(212 N)i + (113 N)j

30. Ejemplo 8. Encuentre los componentes de
una fuerza de 300 N que actúa a lo largo del
manubrio de una podadora. El ángulo con el
suelo es de 320.
F = 300 N
32 o
Fx
32o 320
Fy F Fy
Fx = -|(300 N) cos 320| = -254 N O en notación i,
j:
Fy = -|(300 N) sen 320| = -159 N F = -(254 N)i - (159 N)j

31. Método de componentes
1. Inicie en el origen. Dibuje cada vector a escala
con la punta del 1o a la cola del 2o, la punta del
2o a la cola del 3o, y así para los demás.
2. Dibuje la resultante desde el origen hasta la
punta del último vector y note el cuadrante de la
resultante.
3. Escriba cada vector en notación i, j.
4. Sume algebraicamente los vectores para obtener
la resultante en notación i, j. Luego convierta a
(R, θ).

32. Ejemplo 9. Un bote se mueve 2.0 km al este,
luego 4.0 km al norte, luego 3.0 km al oeste y
finalmente 2.0 km al sur. Encuentre el
desplazamiento resultante.
1. Inicie en el origen. D N 3 km, O
Dibuje cada vector a 2 km, S C B
escala con la punta del 4 km, N
1o a la cola del 2o, la
punta del 2o a la cola A E
2 km, E
del 3o, y así para los
demás.
2. Dibuje la resultante desde el origen hasta la punta
del último vector y note el cuadrante de la resultante.
Nota: La escala es aproximada, pero todavía es
claro que la resultante está en el cuarto cuadrante.

33. Ejemplo 9 (cont.) Encuentre el
desplazamiento resultante.
3. Escriba cada vector N
D 3 km, O
en notación i, j: 2 km, S C B
A = +2 i 4 km, N
B= +4j E
A
C = -3 i 2 km, E
D= -2j 4. Sume algebraicamente
los vectores A, B, C, D
R = -1 i + 2 j para obtener la resultante
en notación i, j.
1 km al oeste y 2 km
1 km al oeste y 2 km 5. Convierta a notación R, θ
al norte del origen..
al norte del origen Vea página siguiente.

34. Ejemplo 9 (cont.) Encuentre desplazamiento
resultante.
N
La suma resultante es: D 3 km, O
2 km, S C B
R = -1 i + 2 j 4 km, N
Ahora encuentre R, θ
E
R = (−1) + (2) = 5
2 2 A
2 km, E
R = 2.24 km
+2 km R Ry = +2
tan φ =
−1 km km
φ
φ = 63.40 N del O Rx = -1 km

35. Recordatorio de unidades significativas:
N
Por conveniencia, D 3 km
siga la práctica de 2 km C B
4 km
suponer tres (3)
cifras significativas E
A
para todos los datos 2 km
en los problemas.
En el ejemplo anterior, se supone que las
distancias son 2.00 km, 4.00 km y 3.00 km.
Por tanto, la respuesta se debe reportar como:
R = 2.24 km, 63.400 N del O
R = 2.24 km, 63.4 N del O

36. Dígitos significativos
para ángulos
Puesto que una décima
de grado con frecuencia R 30 lb
puede ser significativa, a Ry
veces se necesita un
θ
cuarto dígito. Rx 40 lb
Regla: Escriba los
Regla: Escriba los
ángulos a la décima de
ángulos a la décima de Rx 40 lb
θ
grado más cercana. Vea
grado más cercana. Vea
los dos ejemplos
los dos ejemplos φ
siguientes:
siguientes: Ry
R 30 lb
θ = 36.9 ;; 323.1
o
θ = 36.9 323.1
o oo

37. Ejemplo 10: Encontrar R, θ para los tres
desplazamientos vectoriales siguientes:
A = 5 m, 00 C= 0.5
R m
B = 2.1 m, 200 B
θ 200
C = 0.5 m, 900
A=5m B = 2.1 m
1. Primero dibuje los vectores A, B y C a escala
aproximada y los ángulos indicados. (Dibujo burdo)
2. Dibuje la resultante desde el origen hasta la punta
del último vector; note el cuadrante de la resultante.
( R, θ )
3. Escriba cada vector en notación i, j. (continúa...)

38. Ejemplo 10: Encuentre R, θ para los tres
desplazamientos vectoriales siguientes. (Puede
ser útil una tabla.)
Para notación i, j, C= 0.5
encuentre los R m
componentes x, y B
θ 200
de cada vector A,
B, C. A=5m B = 2.1 m
Vector φ componente x (i) componente y (j)
A=5m 00 +5m 0
B = 2.1 m 200 +(2.1 m) cos 200 +(2.1 m) sen 200
C = 0.5 m 900 0 + 0.5 m
R x = Ax + Bx + C x Ry = A y + B y + C y

39. Ejemplo 10 (cont.): Encuentre i, j para
tres vectores: A = 5 m, 00; B = 2.1 m,
200; C = 0.5 m, 900.
componente x (i) componente y (j)
Ax = + 5.00 m Ay = 0
Bx = +1.97 m By = +0.718 m
Cx = 0 Cy = + 0.50 m
4. Sume los vectores A = 5.00 i + 0j
para obtener la B = 1.97 i + 0.718 j
resultante R en
C= 0 i + 0.50 j
notación i, j.
R = 6.97 i + 1.22 j

40. Ejemplo 10 (cont.): Encuentre i, j para tres
vectores: A = 5 m, 00; B = 2.1 m, 200; C = 0.5
m, 900.
R = 6.97 i + 1.22 j Diagrama
para encontrar
5. Determine R, θ a partir R, θ :
de x, y: R Ry
R = (6.97 m) 2 + (1.22 m) 2 θ 1.22 m
Rx= 6.97 m
R = 7.08 m
R = 7.08 m
1.22 m
tan φ = θ = 9.9300 N del E
θ = 9.93 N del E
6.97 m

41. Ejemplo 11: Un ciclista viaja 20 m, E luego 40 m
a 60o N del W, y finalmente 30 m a 210o. ¿Cuál
es el desplazamiento resultante gráficamente?
C = 30 m Gráficamente, se usa
B = 40 regla y transportador
30o
m para dibujar los
componentes, luego
R se mide la resultante
θ 60o R, θ
φ
A = 20 m, E
Sea 1 cm = 10 m R = (32.6 m, 143.0oo))
R = (32.6 m, 143.0

42. A continuación se proporciona una
comprensión gráfica de los
componentes y la resultante:
Nota: Rx = Ax + Bx + Cx
Cy
By 30o 0
C B R y = Ay + By + C y
R
Ry θ
φ 60o A
Rx Ax
Cx Bx

43. Ejemplo 11 (cont.) Use el método de
componentes para encontrar la resultante .
Escriba cada vector
C By
en notación i, j.
30o
y
C B Ax = 20 m, Ay = 0
R
Ry A = 20 i
φ θ 60 A
Bx = -40 cos 60o = -20 m
Rx A
C Bx x
By = 40 sen 60o = +34.6 m
x
B = -20 i + 34.6 j
Cx = -30 cos 30o = -26 m
Cy = -30 sen 60o = -15 m C = -26 i - 15 j

44. Ejemplo 11 (cont.) Método de componentes
Sume
C B algebraicamente:
A = 20 i
y 30o
y
C B
B = -20 i + 34.6 j
R
Ry θ 60 A C = -26 i - 15 j
φ
Rx A R = -26 i + 19.6 j
C Bx x
x
R= (-26)2 + (19.6)2 = 32.6 m
+19.6 R
19.6
φ tan φ = θ = 143oo
θ = 143
-26 -26

45. Ejemplo 11 (cont.) Encuentre la resultante.
R = -26 i + 19.6 j
C B
y 30o
y
C B
R +19.6 R
Ry θ φ
φ 60 A
-26
Rx A
C Bx x
x
El desplazamiento resultante del ciclista se proporciona
mejor mediante sus coordenadas polares R y θ.
R = 32.6 m; θ = 14300
R = 32.6 m; θ = 143

46. Ejemplo 12. Encuentre A + B + C para los
vectores que se muestran a continuación.
B Cx
A = 5 m, 900 350 Cy
B = 12 m, 00 A y
θ C
C = 20 m, -350
R
Ax = 0; Ay = +5 m
A = 0 i + 5.00 j
Bx = +12 m; By = 0 B = 12 i + 0 j
Cx = (20 m) cos 350 C = 16.4 i – 11.5 j
Cy = -(20 m) sen -350 R = 28.4 i - 6.47 j

47. Ejemplo 12 (cont.). Encuentre A + B + C
B Rx = 28.4 m
350 θ
A
C R
θ
R Ry = -6.47 m
R = (28.4 m) + (6.47 m)
2 2
R = 29.1 m
R = 29.1 m
6.47 m
tan φ = θ = 12.800 S del E
θ = 12.8 S del E
28.4 m

48. Diferencia vectorial
Para vectores, los signos indican la dirección. Por
tanto, cuando se resta un vector, antes de sumar
se debe cambiar el signo (dirección).
Considere primero A + B gráficamente:
R=A+B
B
R
B
A A

49. Diferencia vectorial
Para vectores, los signos indican la dirección. Por
tanto, cuando se resta un vector, antes de sumar
se debe cambiar el signo (dirección).
Ahora A – B: primero cambie el signo
(dirección) de B, luego sume el vector negativo.
B -B A
R’ -B
A A

50. Suma y resta
La resta resulta en un diferencia significativa tanto
en la magnitud como en la dirección del vector
resultante. |(A – B)| = |A| - |B|
Comparación de suma y resta de B
R=A+B R’ = A - B
B
A
R
B R’ -B
A A

51. Ejemplo 13. Dados A = 2.4 km N y B = 7.8
km N: encuentre A – B y B – A.
A - B B - A
A – B;
B-A +A -A
+B
-B
R R
A B (2.43 N – 7.74 S) (7.74 N – 2.43 S)
2.43 N 7.74 N
5.31 km, 5.31 km,
S N

52. Resumen para vectores
 Una cantidad escalar se especifica
completamente sólo mediante su magnitud. (40
m, 10 gal)
 Una cantidad vectorial se especifica completamente
mediante su magnitud y dirección. (40 m, 300)
Componentes de R:
R
Ry
Rx = R cos θ θ
Ry = R sen θ Rx

53. Continúa resumen:
 Encontrar la resultante de dos vectores
perpendiculares es como convertir de coordenadas
polares (R, θ) a rectangulares (Rx, Ry).
Resultante de vectores:
R
R= x +y2 2
Ry
θ
y
tan θ = Rx
x

54. Método de componentes para
vectores
 Inicie en el origen y dibuje cada vector en
sucesión para formar un polígono etiquetado.
 Dibuje la resultante desde el origen hasta la
punta del último vector y note el cuadrante de
la resultante.
 Escriba cada vector en notación i, j (Rx, Ry).
 Sume algebraicamente los vectores para
obtener la resultante en notación i, j. Luego
convierta a (R, θ).

55. Diferencia vectorial
Para vectores, los signos indican dirección. Por
tanto, cuando se resta un vector, antes de sumar
se debe cambiar el signo (dirección).
Ahora A – B: primero cambie el signo
(dirección) de B, luego sume el vector negativo.
B -B A
R’ -B
A A

56. EJERCICIO Nº1
Realizar los siguientes ejercicios
→ → → → → → → →
A = 3 i + 4 j + 2 k; B = i + 3 j − 5 k
→ → → → →
a) A + B b) A − B c)2 A
→ → → → →
a) A + B = 4 i + 7 j - 3 j
→ → → → →
b) A − B = 2 i + j + 7 k
→ → → →
c)2 A = 6 i + 8 j + 4 k

57. EJERCICIOS
Dado el vector A=(12,-5).Encontrar el vector unitario que tiene
la misma dirección que “A” y el vector unitario que tiene a la
dirección opuesta de “A”.
Modulo del vector A=(12,-5)
→
A = 12 2 + (−5) 2 = 169 = 13
→ → → → →
→ A 12 i − 5 j 12 i 5 j
a) μ = →
= = −
13 13 13
A
→ → → → →
→ A (12 i − 5 j ) - 12 i 5 j
b) ν = − →
=− = +
13 13 13
A

58. PRODUCTO ENTRE VECTORES
Existen dos formas de multiplicar vectores, siendo
una denominada producto escalar y el otro
producto vectorial.
PRODUCTO ESCALAR.-Dados dos vectores, su producto
escalar se define como el producto de sus módulos por el coseno
del ángulo que forman .
→ →
A• B = ABcosθ
→ → → →
Propiedad conmutativa A•B = B• A
→ → → → → → →
A• (B+ C) = A•B+ A• C
Propiedad asociativa
→ → → → → →
m( A• B) = (m A ) • B = A• (m B)

59. Ejemplo: Determinar el ángulo entre los
vectores
→ → → → → → → →
A = 3 i + 4 j + 2 k; B = i + 3 j − 5 k
→ →
Angulo entre ellos: A• B = 3(1) + 4(3) + 2(− 5) = 5
A = 32 + 4 2 + 2 2 = 39 = 5,4;B = 12 + 32 + (− 5)2 = 35 = 5,9
→ →
A• B 5
θ = ar cos = ar cos ar cos(0,16) = 81°
AB (5,4)(5,9)

60. GRACIAS…