El documento analiza la correlación entre diferentes variables cuantitativas mediante el cálculo del coeficiente de correlación de Pearson en tres ejercicios. En el primer ejercicio no se encuentra correlación entre el peso y horas de deporte. En el segundo ejercicio sí existe una alta correlación negativa entre cigarrillos fumados y nota de acceso. En el tercer ejercicio no se encuentra correlación entre la nota de matemáticas y lengua.

1. Seminario 10

2. 1.1.- Utilizando nuestra base de datos comprueba la
correlación entre la variable peso y la variable horas
de dedicación al deporte. Comenta los resultados.
Para ver si hay correlación entre el peso y las horas
primero vamos a formar un gráfico de dispersión
para ver si existe alguna correlación a simple vista.
Como realizar el gráfico:

3. gráfico
Cuadro de
díalogos
antiguos
Dispersión/punto
Dispersión
simple

4. Y obtenemos esta gráfica, por lo que ha simple
vista no hay correlación.

5. Cremos las hipótesis:
Ho: no hay correlación entre las dos variables
H1 : si hay correlación en las dos variables
Para hallar la correlación seguimos el siguiente
procedimiento:

6. analizar correlación bivariadas

7. Seleccionamos las dos variables: peso y horas
de dedicación, seleccionamos coeficiente de
corelación de Pearson, prueba de significación
bilateral y marcar la correlación significativa;
Posteriormente en los resultados nos aparecerá
la correlación.

9. Vemos que la correlación de 0,41.
Como el p valor es 0,91 y el nivel de significación
0,05 aceptamos la hipótesis nula, por lo que no
hay una correlación entre estas dos variables.

10. 1.2.- Calcula el Coeficiente de Correlación de Pearson para las
variables no de cigarrillos fumados al día y nota de acceso.
Comenta los resultados.
Tras seguir el mismo procedimiento anterior Vemos que el coeficiente
de correlación de Pearso es -0,976 por lo que es alto
p valor es 0,001 por lo que es menor del nivel de significación lo que
quiere decir que si hay correlación entre la nota de acceso al grado y el
número de cigarrillos fumados al día

11. 1.3.-Calcula el Coeficiente de Correlación de
Pearson para las variables peso y altura (limitando la
muestra a 10 casos). Comenta los resultados.
Primero al ser 10 casos tenemos que ver si sigue una
distribución normal, para estorealizamos el test de
kolmogorov

13. Seleccionamos las variables que queremos y ya
nos aparece que la muestra sigue una
distribución normal.

14. A continuación calculamos el diagrama de dispersión
de variables de peso y altura para ver si tiene
correlación a simple vista las variables.

16. Como observaos en la imagen no se ve apenas
correlación entre ambas variables pero para
estar seguro calculamos el coeficiente de
correlación de Pearson mediante SPSS.

17. Con los datos obtenidos por este
programa, vemos que el coeficiente de
correlación de Pearson es
positivo,, o,668, siendo elevado, por lo que
existe correlación entre la variable altura y peso;
Para saber cual de las hipótesis es la verdadera
nos fijamos en el valor p que en este caso es
0,000, al ser menor este valor que el nivel de
significación 0,05 podemos decir que aceptamos
la hipótesis alternativa y por tanto si existe
correlación entre la altura y el peso en la
población.

18. Ejercicio S10.2: De una muestra de niños conocemos su edad
(X) medida en días y su peso (Y) en kg., según los resultados de
la tabla. Si ambas variables se distribuyen normalmente,
averiguar si existe correlación entre ambas variables en la
población de donde proviene la muestra?
Tenemos dos variables cuantitativas “edad” y “peso” que
se distribuyen normalmente, por lo que tenemos que:
1. Calcular el coeficiente de correlación de Pearson
2. Averiguar si el coeficiente de correlación es significativo

19. Al conocer que son variables que se distribuyen
normalmente, son cuantitativas, aplicamos el
coeficiente R decorrelación de pearson.
Para comenzar construimos una tabla para así
poder conocer rxy, usamos la variable “edad” = x
y la variable “peso”= y

21. A partir de esta tabla calculamos rxy a partir de la
siguiente formula:
Podemosver que hay una relación de correlación
entre el peso y la edad debido a que el
coeficiente de correlación de Pearson es alta.

22. Una vez obtenido el valor de Rxy establecemos
las hipótesis:
Ho: no hay correlación en la población entre la
edad medida en días y el peso.
H1: si hay correlación en la población entre la
edad medida en días y el peso.

23. Para saber que hipótesis es la que tenemos que
aceptar empezamos calculando Tn-2, cuya
fórmula es :

24. Una vez obtenido el resultado de Tn-2 , es 9,6
averiguamos el punto crítico, con un grado de
libertad de n-2 = 19, y un nivel de significación
de 0,05, tras buscarlo en la tabla obtenemos:
2, 093.

26. Al conocer que el estadístico es mayor que el
punto crítico, aceptamos la hipótesis alternativa y
rechazamos la hipótesis nula. Por lo que existe
una relación entre la edad y el peso en la
población.
9,6 > 2,09, Tn-2 > T0,05;19

27. Ejercicio S10.3: De una muestra de alumnos conocemos las
notas de Matemáticas (X) y de Lengua (Y), según los resultados
de la tabla. Si ambas variables se distribuyen normalmente,
averiguar ¿existe correlación entre ambas variables en la
población de donde proviene la muestra?
Tenemos dos variables cuantitativas “nota de
matemáticas” y “nota de lengua” que se distribuyen
normalmente, por lo que tenemos que:
1. Calcular el coeficiente de correlación de Pearson
2. Averiguar si el coeficiente de correlación es significativo

28. Al igual que en el ejercicio anterior construimos
una tabla con las variables cualitativas para
poder calcular así rxy y ver si existe correlación
entre estas variables cuantitativas.
Primero empezamos construyendo una tabla
para poder utilizar la fórmula:

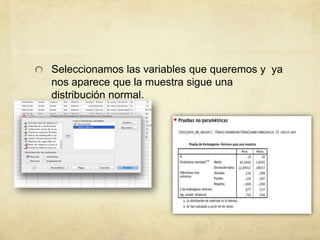
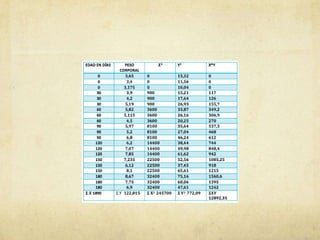
30. Realizamos la fórmulas de Pearson con los datos
obtenidos:
RXY=(7(140)-28(35)]/ [7(140)-282 )*(7(173)-
352)= 0
El coeficiente de correlación de Pearson nos sale
cero, por lo que no hay correlación entre las
variables en la muestra.

31. A continuación establecemos las dos hipótesis
Ho: no hay correlación entre las variables en la
población.
H1: si hay correlación entre las variables en la
población.
Para calcular el estadístico y poder rechazar o
aceptar las hipótesis realizamos la siguiente
formula:

32. Tn-2 = 0, obtenemos este resultado debido a que Rxy ya ha
dado 0, por lo que al realizar el producto de la fórmula el
resultado es cero. Una vez con el resultado del estadístico
intentamos averiguar el valor del punto crítico para
poder aceptar una de las hipótesis.

33. Ahora para obtener el punto crítico tengo que
conocer el grado de libertad y el nivel de
significación:
Dado que no me dan el nivel de
significación, cogemos un nivel de confianza del
95%, o lo que es igual un nivel de significación de
0,05,
El grado de libertad= n-2, por lo que es igual a 7-2=
5,

35. Tras buscar en la tabla vemos que el punto crítico
es 2,57.
Al ser mayor el punto crítico que el estadístico (Tn-
2), y con un nivel de significación de 0,05
concluimos que se aceptaría la Ho y se rechazaría
la H1.
No hay correlación entre las notas de matemáticas
y de lengua en la población.