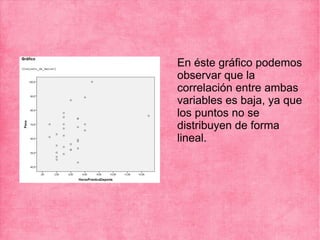
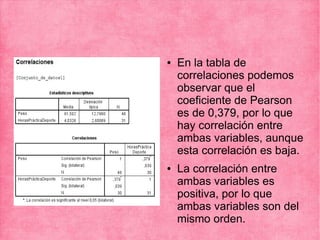
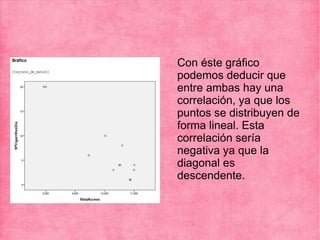
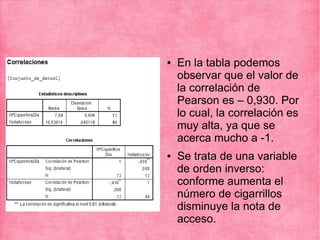
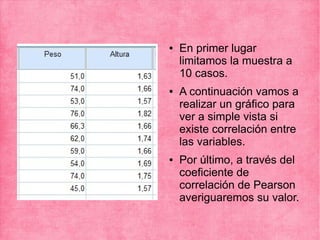
El documento presenta los resultados de varios ejercicios sobre el cálculo del coeficiente de correlación de Pearson entre diferentes variables. En el ejercicio 1 se analiza la correlación entre peso y horas de deporte, encontrando una correlación baja y positiva. En el ejercicio 2 se encuentra una alta correlación negativa entre cigarrillos y nota. En el ejercicio 3 se reporta una alta correlación positiva entre peso y altura en una muestra limitada. Finalmente, en el ejercicio 4 no se encuentra correlación entre notas de matemáticas y lengua.

1. Seminario 10

2. Ejercicio 1.1
Utilizando nuestra base de datos comprueba la
correlación entre la variable peso y la variable
horas de dedicación al deporte. Comenta los
resultados.
En primer lugar pasamos los datos de la base de datos a
SPSS. Utilizamos el coeficiente de correlación de Pearson para
averiguar si hay correlación entre ambas, realizando previamente
un gráfico.

3. En éste gráfico podemos
observar que la
correlación entre ambas
variables es baja, ya que
los puntos no se
distribuyen de forma
lineal.

4. ● En la tabla de
correlaciones podemos
observar que el
coeficiente de Pearson
es de 0,379, por lo que
hay correlación entre
ambas variables, aunque
esta correlación es baja.
● La correlación entre
ambas variables es
positiva, por lo que
ambas variables son del
mismo orden.

5. Ejercicio 1.2
Calcula el coeficiente de correlación de
Pearson para las variables número de cigarrillos
al día y nota de acceso. Comenta los resultados.
En primer lugar realizamos un gráfico para comprobar si hay
correlación entre ambas a simple vista.

6. Con éste gráfico
podemos deducir que
entre ambas hay una
correlación, ya que los
puntos se distribuyen de
forma lineal. Esta
correlación sería
negativa ya que la
diagonal es
descendente.

7. ● En la tabla podemos
observar que el valor de
la correlación de
Pearson es – 0,930. Por
lo cual, la correlación es
muy alta, ya que se
acerca mucho a -1.
● Se trata de una variable
de orden inverso:
conforme aumenta el
número de cigarrillos
disminuye la nota de
acceso.

8. Ejercicio 1.3
Calcula el coeficiente de correlación de
Pearson para las variables peso y altura
(limitando la muestra a 10 casos). Comenta los
resultados.

9. ● En primer lugar
limitamos la muestra a
10 casos.
● A continuación vamos a
realizar un gráfico para
ver a simple vista si
existe correlación entre
las variables.
● Por último, a través del
coeficiente de
correlación de Pearson
averiguaremos su valor.

10. A simple vista podemos
ver que hay correlación
entre ambas variables.
La correlación sería
positiva porque la
diagonal es ascendente.

11. ● En la tabla de
correlaciones
observamos que la
correlación de Pearson
es de 0,757. Por lo que
se trata de una
correlación alta entre
ambas variables.
● Al ser una correlación
positiva, ambas
variables son del mismo
orden.

12. Ejercicio 1.4
Muestra los gráficos en una de las correlaciones

14. Ejercicio 2
En una muestra de niños conocemos su edad (x)
medida en días y su peso (y) medido en kg. Si
ambas variables se distribuyen normalmente,
averiguar si existe correlación entre ambas
variables en la población de donde proviene la
muestra.

16. Averiguamos la correlación de Pearson:
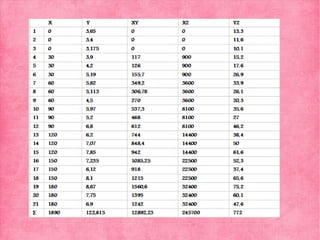
Rxy= (21x 12892,23) – (1890x 122,815) / √[((21x 245700) – (1890)2) x ((21x
772) - ( 122,815) 2 )] =0,91
Al sustituir los datos en la fórmula nos da una correlación de 0,91. Por lo que se
trata de una correlación positiva muy alta.

17. Cálculo de la significación:
Para ello contrasto las hipótesis:
H0=la correlación es cero
H1= hay correlación entre ambas variables
t n-2= 0,91 x √((0,91 -2)/ (1-0,912))= 9,6
●Tras sustituir los valores en la fórmula obtengo un resultado de t
n-2= 9,6. Al no tener el valor de alfa, uso alfa=0,05 y obtengo que t
0,05;19= 2,093.
●Como t n-2>t 0,05;19 → se acepta la hipotesis alternativa y se
rechaza la nula.

18. Ejercicio 3
De una muestra de alumnos conocemos las notas
de Matemáticas (X) y Lengua (Y). Si ambas
variables se distribuyen normalmente, averiguar si
existe correlación entre ambas variables en la
población de la que viene la muestra.

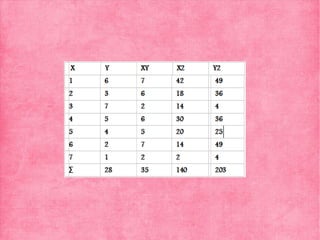
20. Averiguamos el coeficiente de correlación de
Pearson:
Rxy= (7x140)-(28x35)/ √[((7x140)-(2822))x((7x203)-(3522))]= 0
Como su resultado es 0 indica que no hay correlación
entre ambas variables.

21. Cálculo de la significación:
Para ello contrasto las hipótesis:
H0=la correlación es cero
H1= hay correlación entre ambas variables
t n-2= 0x√[(7-2)/(1-0)2]= 0
●Al sustituir los resultados de la fórmula nos da 0. Como no
tenemos el valor de alfa, establecemos que alfa= 0,05. Dando
como resultado t 0,05;19= 2,57.
●Por tanto, t n-2< t 0,05;19 → aceptamos la hipótesis nula y
rechazamos la hipótesis alternativa.