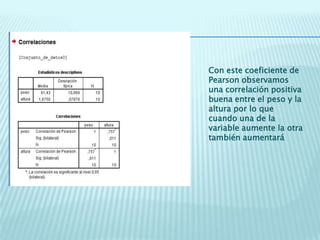
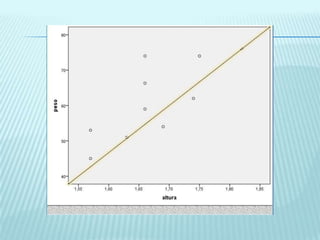
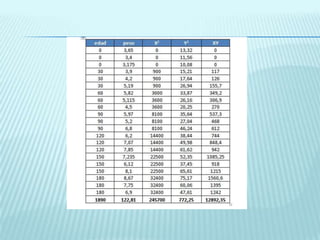
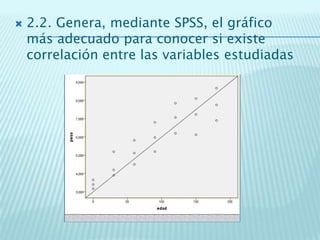
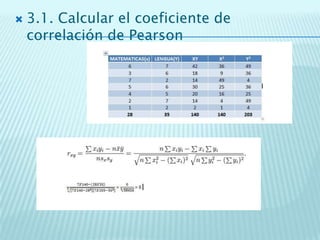
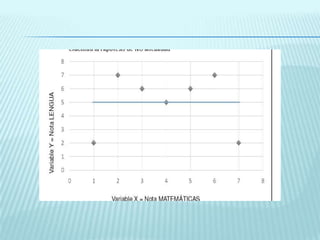
1. Se analizan las correlaciones entre diferentes variables como peso y horas de deporte, número de cigarrillos y nota de acceso, peso y altura, y peso y edad en días. En general se observan correlaciones positivas bajas o buenas, indicando que cuando aumenta una variable la otra tiende a aumentar ligeramente. 2. Se calcula el coeficiente de correlación de Pearson entre las notas de Matemáticas y Lengua de un grupo de alumnos para determinar si existe una correlación significativa entre ambas variables en la población de la que proviene la muestra.

1. SEMINARIO 10
CORRELACIÓN

2. EJERCICIO 10. 1
 1.1.- Utilizando nuestra base de datos
comprueba la correlación entre la
variable peso y la variable horas de
dedicación al deporte. Comenta los
resultados.

7. Con este coeficiente de Pearson observamos una
correlación positiva baja entre las horas de práctica
de deporte y el peso. Por lo que cuando una de las
variables aumenta la otra aumentará ligeramente.

8.  1.2.- Calcula el Coeficiente de
Correlación de Pearson para las
variables nº de cigarrillos fumados al
día y nota de acceso. Comenta los
resultados.

12. Con este coeficiente de Pearson observamos
una correlación negativa baja entre el numero
de cigarrillos y la nota de acceso por lo que
cuando una de las variables aumenta la otra
descenderá ligeramente.

13.  1.3.- Calcula el Coeficiente de
Correlación de Pearson para las variables
peso y altura(limitando la muestra a 10
casos). Comenta los resultados.

16. Con este coeficiente de
Pearson observamos
una correlación positiva
buena entre el peso y la
altura por lo que
cuando una de la
variable aumente la otra
también aumentará

17.  1.4.- Muestra los gráficos en una de
las correlaciones.

21. EJERCICIO 10.2
 De una muestra de niños conocemos su
edad medida en días y su peso en kg.,
según los resultados de la tabla. Si
ambas variables se distribuyen
normalmente:
2.1. Averiguar si existe correlación entre
ambas variables en la población de
donde proviene la muestra

23. Con este coeficiente de Pearson podemos
observar una correlación casi perfecta positiva
entre el peso y la edad en días por lo que cada
vez que aumenta una de las variables
aumentará la otra.

24.  2.2. Genera, mediante SPSS, el gráfico
más adecuado para conocer si existe
correlación entre las variables estudiadas

25.  2.3. ¿Es significativo el coeficiente de
correlación hallado?
Para saber si es significativo o no
tenemos que hallar la t de Student

27. EJERCICIO 10.3
 Ejercicio S10.3: De una muestra de
alumnos conocemos las notas de
Matemáticas (X) y de Lengua (Y), según
los resultados de la tabla. Si ambas
variables se distribuyen normalmente,
averiguar si existe correlación entre
ambas variables en la población de
donde proviene la muestra?

28.  3.1. Calcular el coeficiente de
correlación de Pearson

30.  3.2. Averiguar si el coeficiente de
correlación es significativo

31. FIN