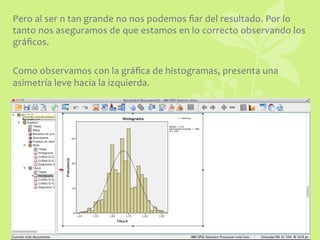
Este documento presenta un análisis estadístico que estudia la relación entre el peso y la talla de individuos utilizando la correlación de Pearson. Se establecen hipótesis y se comprueban los supuestos de linealidad y normalidad antes de calcular el coeficiente de correlación. Los resultados muestran una correlación positiva alta y significativa entre las variables. También se realizan otras pruebas estadísticas como la correlación biserial puntual.

1. SEMINARIO
X
Adelaida
Aceituno
Domínguez
Subgrupo5,
HHUU
Virgen
del
Rocío
ESTADISTICA
Y
TICS

2. CORRELACIÓN
DE
PEARSON
Estamos
ante
dos
variables
cuantitativas,
que
son
peso
y
talla.
Establecemos
nuestras
hipótesis
de
investigación:
• Hipótesis
alternativa:
¿existe
relación
entre
ambas
variables?
• Hipotesis
nula:¿
no
existe
relación
entre
ambas
variables?
Usamos
el
coeficiente
de
correlación
de
Pearson.
Primero
hay
que
ver
si
se
cumplen
las
dos
asunciones,
que
son:
• Que
tengan
relación
lineal:
lo
comprobamos
mediante
grafico
de
dispersión.
Vemos
como
la
nube
de
puntos
sigue
la
relación
lineal.
•
Que
cumpla
el
criterio
de
normalidad:
la
observamos
estableciendo
gráficos
con
nuestras
variables.

3. Podemos
observar
como
existe
una
relación
lineal
en
la
dispersión
de
la
nube
de
puntos.

4. Para
estudiar
si
cumple
el
criterio
de
normalidad,
lo
observamos
estableciendo
gráficos
con
nuestras
variables.
Pruebas
de
normalidad
Establecemos
hipótesis
alternativa:
¿Existe
diferencia
entre
nuestra
distribución
y
la
normal?
Hacemos
lo
mismo
estableciendo
nuestra
hipótesis
nula:
¿No
existe
diferencias
con
la
distribución
normal?
Usamos
las
pruebas
de
kolmogorov-­‐
smirnov
ya
que
la
n
es
mayor
de
30.
Tras
esto,
vemos
los
resultados
en
tablas
de
nuestra
prueba
de
normalidad,
fijándonos
en
los
valores
que
nos
ha
dado
la
significación.

5. Podemos
observar
que
el
valor
de
sig.
Es
inferior
a
0,5
por
lo
que
rechazamos
la
hipótesis
nula
y
nos
quedamos
con
la
hipótesis
alternativa.
Por
lo
tanto
diríamos
que
nuestra
distribución,
atendiendo
al
resultado
de
la
prueba
estadística
es
diferente
a
la
normal.

6. Pero
al
ser
n
tan
grande
no
nos
podemos
fiar
del
resultado.
Por
lo
tanto
nos
aseguramos
de
que
estamos
en
lo
correcto
observando
los
gráficos.
Como
observamos
con
la
gráfica
de
histogramas,
presenta
una
asimetría
leve
hacia
la
izquierda.

7. Basándonos
en
el
gráfico
Q
vemos
que
la
distribución
es
muy
parecida
a
la
normal.

8. Lo
mismo
ocurre
con
el
diagrama
de
cajas.
Se
ve
similitud
con
la
normal
pero
con
una
leve
asimetría
hacia
el
peso,
como
también
se
observaba
en
los
anteriores.
El
mismo
diagrama
nos
informa
de
que
existe
un
pico
en
el
valor
24.
podemos
rechazarlo
sin
nos
altera
mucho
la
distribución.

9. Simétrico,
con
algunos
picos,
pero
sin
importancia.
Por
tanto,
concluimos
que
cumple
la
normalidad,
cumple
la
segunda
asunción,
por
lo
que
podemos
usar
la
correlación
de
Pearson.

10. Realizamos
la
correlación
de
Pearson.

11. Tenemos
una
tabla
de
doble
salida,
ya
que
la
información
está
repetida.
Nos
da
una
correlación
de
1,
es
decir,
correlación
perfecta.
Vemos
que
la
relación
entre
peso
y
talla
es
de
0,646,
es
decir,
es
una
correlación
alta,
ya
que
es
mayor
de
0,5.
Y
además
se
trata
de
una
relación
positiva,
es
decir,
que
cuanto
más
peso,
más
talla.
La
N
varía:
545
han
contestado
la
variable
peso;
339
han
contestado
al
variable
talla;
549
han
contestado
ambas
variables
por
ultimo
vemos
que
presenta
una
significación
menos
de
0,5,
aceptamos
la
hipótesis
alternativa.

12. Realizamos
también
otras
pruebas
no
paramétricas
• En
la
tau_b
de
kendall,
p
disminuye.
Es
un
poco
menor
de
0,5.
Esto
es
debido
a
que
es
más
conservadora.
Es
una
manera
de
disminuir
el
error
tipo
1.
No
asume
el
riesgo
de
rechazar
la
hipótesis
nula.
• Las
pruebas
Rho
de
spearman
es
más
potente.
Son
menos
conservadoras.
Dando
p>0,5.
Esta
también
se
utiliza
con
variables
ordinales

14. CORRELACION
BISERIAL
PUNTUAL
Cuando
relacionamos
variable
ordinal
con
variable
cuantitativa.
• Establecemos
como
variable
dicotómica
sexo.
• Como
variable
continua:
frecuencia
de
ejercicio
físico.
A
continuación
establecemos
nuestra
variable
alternativa
y
nula:
• Variable
alternativa:
¿existe
relación
entre
el
sexo
y
la
frecuencia
de
actividad
física?
• Hipótesis
nula:
no
existe
relación.
Establecemos
la
correlación.

15. Como
nuestra
N
es
muy
grande,
podemos
considerar
que
presentación
una
distribución
normal.
Pero
si
queremos
asegurarnos
podemos
usar
los
gráficos
como
el
histograma,
diagrama
de
cajas…etc,
y
observarlo.
Tenemos
una
relación
negativa
de
tamaño
medio
(0,303).
Aceptamos
la
hipótesis
alternativa.
Para
estudiar
más
a
fondo
esa
relación
negativa
vemos
como
está
etiquetada
(1-­‐chico;
2-­‐chica).
Podemos
concluir
que
la
relación
negativa
nos
indica
que
cuando
más
sexo
(chicas),
menos
actividad
física
se
realiza.

16. Correlacion
de
Phi/
coeficiente
de
contingencia
/
V
de
cramer.
Para
relacionar
variables
categóricas.
Se
utilizan
para
tablas
de
2x2.
• Correlación
de
Phi:
cuando
las
dos
variables
son
dicotómicas.
• Coeficiente
de
contingencia
o
V
de
cramer:
puede
haber
más
categorías.
Aunque
una
sea
dicotómica
pero
la
otra
no.
Ejemplo:
establecemos
nuestra
hipotesis
alternativa
y
nula.
• H.
Alternativa:
¿existe
relación
entre
el
sexo
y
haber
consumido
tabaco?
• H.
Nula:
no
existe
relación.

17. Vamos
a
usar
el
coeficiente
de
Phi.
Vemos
como
nos
da
un
valor
de
0,019.
La
significación
nos
da
mayor
de
0,5,
por
lo
que
rechazamos
nuestra
hipótesis
alternativa
y
aceptamos
la
nula.
Por
lo
tanto,
no
existe
relación
entre
el
sexo
y
el
consumo
de
tabaco.

18. Relacionamos
variables
no
dicotómicas.
Relacionamos
el
grado
de
funcionalidad
familiar
(Apgar),
que
se
categoriza
en
3:
• Normofuncional
• Disfuncional
leve
• Disfuncional
grave.
Con
la
frecuencia
de
consumo
de
tabaco.

19. • Vemos
que
existe
relación
ya
que
p
es
menos
de
0,5.
el
coeficiente
de
contingencia
se
encuentra
entre
bajo
y
medio.
En
V
de
cramer
es
más
bajo
que
en
el
anterior.
• Para
observar
la
relación
entre
F.
Esperadas
y
las
F.
Observadas
observamos
la
tabla
donde
quedan
plasmadas
estas.