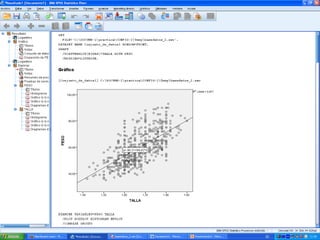
Este documento presenta los pasos para analizar la relación entre el peso y la talla en una muestra de adolescentes. Propone utilizar la prueba R de Pearson debido a que las variables son cuantitativas, pero primero comprobar la relación lineal y distribución normal mediante gráficos. Los resultados muestran una relación lineal positiva y una distribución normal levemente asimétrica. La correlación entre peso y talla es alta y positiva. Por lo tanto, se acepta la hipótesis alternativa de que existe una relación entre el peso y