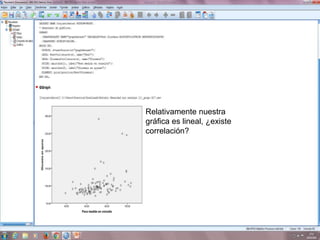
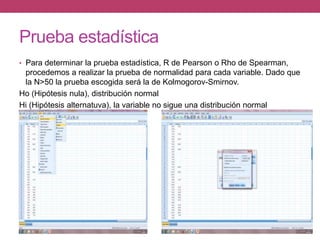
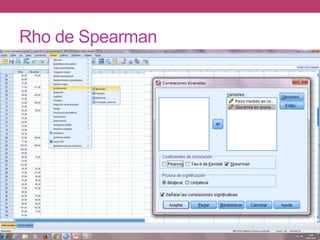
El documento describe cómo realizar pruebas estadísticas para determinar la correlación entre dos variables, peso y glucemia. Se realizan pruebas gráficas y estadísticas como la R de Pearson y Rho de Spearman. Los resultados muestran que existe una correlación positiva entre el peso y la glucemia, es decir, que el peso influye en los niveles de glucemia. Sin embargo, no se encontró evidencia de correlación entre la presión arterial sistólica y los niveles de colesterol.

1. SEMINARIO 9
Correlación entre variables peso y glucemia
Patricia Cabrera Domínguez. Subgrupo 17

2. Correlación entre variables
La correlación estadística determina la relación o dependencia que existe
entre las dos variables que intervienen en una distribución bidimensional.
Para estudiar la correlación entre variables debemos hacer una prueba gráfica
y una prueba estadística.
Si efectivamente existe relación la prueba gráfica será linear pero para
asegurarnos también procederemos a realizar una prueba estadística.
Para estudiar la correlación las pruebas estadísticas utilizadas son la R de
Pearson y la Rho se Spearman. Para seleccionar la prueba correcta debemos
de determinar si las variables siguen una distribución normal o no. En el caso
de que efectivamente sigan una distribución normal la prueba utilizada sería la
R de Pearson, en caso contrario, la Rho de Spearman.
Para determinar si las variables siguen una distribución normal realizamos la
prueba de normalidad de Saphiro- Wilks, si la muestra es <50 o Kolmogorov-
Smirnov, si la muestra es >50
La hipótesis nula, sería que no existe correlación. El peso no influye en el nivel
de glucemia y viceversa.
La hipótesis alternativa, si existe correlación. El peso influye en el nivel de
glucemia y viceversa.

3. Generamos un gráfico de dispersión
simple

4. Relativamente nuestra
gráfica es lineal, ¿existe
correlación?

5. Prueba estadística
• Para determinar la prueba estadística, R de Pearson o Rho de Spearman,
procedemos a realizar la prueba de normalidad para cada variable. Dado que
la N>50 la prueba escogida será la de Kolmogorov-Smirnov.
Ho (Hipótesis nula), distribución normal
Hi (Hipótesis alternatuva), la variable no sigue una distribución normal

6. Dado que la significación en ningún caso es mayor al
valor 0,05, rechazamos la hipótesis nula y aceptamos la
alternativa, las variables no siguen una distribución normal
Por tanto utilizamos la Rho de Spearman

7. Rho de Spearman

8. Nuestro margen de error es de 0,05, dado que la significación es menor que el mismo,
al rechazar la hipótesis nula y aceptar la alternativa no corremos ningún riesgo, por
tanto podríamos decir que existe correlación entre ambas variables, el peso influye en
el nivel de glucemia.
Incluso nuestro margen de error podría haber sido de 0,01.

9. Correlación entre PAS y Colesterol

10. • Ho: No existe correlación. Los niveles de presión arterial sistólica no influyen en los niveles de colesterol y viceversa.
• Hi: Existe correlación. Los niveles de presión arterial sistólica influyen en los niveles de colesterol y viceversa.
• A continuación realizamos los mismos pasos que en la correlación anterior.
La dispersión de la gráfica
no es lineal, podríamos
decir que no existe
correlación

11. Prueba Rho de Spearman.
Dado los valores de significación aceptamos la Hipótesis
alternativa, no existe distribución normal.

12. De nuevo existe correlación, rechazamos la hipótesis nula, aceptamos la hipótesis alternativa, Hi: Existe correlación. Los niveles de
presión arterial sistólica influyen en los niveles de colesterol y viceversa. Nuestro margen de error establecido es de 0,05 pero
incluso podría ser de 0,01. Al aceptar la hipótesis alterativa corremos un único riesgo de 0,007.