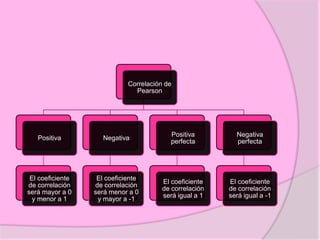
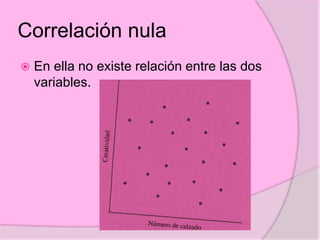
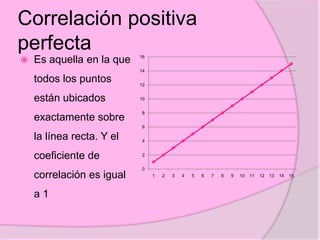
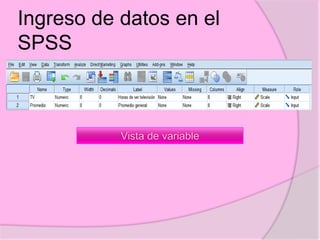
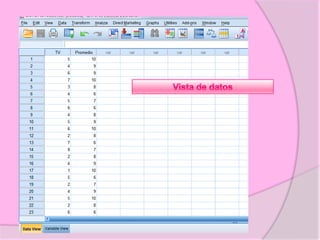
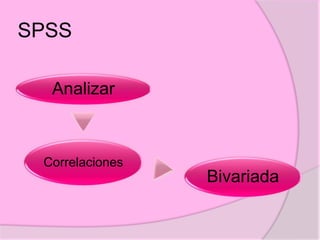
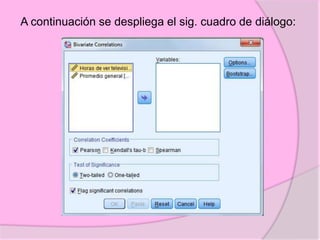
Este documento define diferentes tipos de correlación como la correlación de Pearson, Kendall y Spearman. Explica que la correlación de Pearson mide la relación sistemática entre dos variables continuas, mientras que Kendall y Spearman se usan para variables ordinales o de rangos. También describe correlaciones positivas, negativas, nulas y perfectas, e ilustra cómo se representan gráficamente. Además, brinda detalles sobre cómo calcular e interpretar los coeficientes de correlación.

2. Definición
 Una correlación es una relación de
variables.

3. Correlación
Pearson
Kendall
Sperarman

4. Correlación de Pearson.
 Cambio sistemático en las
puntuaciones de dos variables de
intervalo o razón.

5.  Para esta prueba necesario formular las
variables en modo de Independiente y
Dependiente, sin embargo la correlación no
determina que una variable sea causa y la
otra efecto, por ejemplo existe correlación
entre altura y peso pero jamás podremos
asegurar que la altura es la causa del peso.

6. Correlación de
Pearson
Positiva
El coeficiente
de correlación
será mayor a 0
y menor a 1
Negativa
El coeficiente
de correlación
será menor a 0
y mayor a -1
Positiva
perfecta
El coeficiente
de correlación
será igual a 1
Negativa
perfecta
El coeficiente
de correlación
será igual a -1

7. Correlación positiva
 Es cuando los valores altos coinciden
con los valores altos, los valores bajos
con los bajos y los medianos con los
medianos.

8.  Dicho de otra forma cuando la variable A
incrementa la variable B incrementa en la
misma proporción, la variable A es
directamente proporcional a la variable B

10. Hipótesis
 A mayor número de horas de estudio
mayor será la calificación del examen.
Menor número de horas de estudio menor
será la calificación del examen.

11. Diagrama de dispersión
 La gráfica para representar a la
correlación es el diagrama de
dispersión.

12. Correlación positiva
 Nótese cómo la línea va subiendo de
izquierda a derecha.

13. Correlación negativa
 Es aquella en donde los valores altos
coinciden con los valores bajos y
cuando los valores bajos coinciden con
los altos.

14.  La variable A es inversamente
proporcional a la variable B. Es
decir, cuando la variable A incrementa
la variable B decrementa en la misma
proporción.

16. Hipótesis
 A mayor asertividad menor será el
porcentaje de relaciones fallidas. A
menor asertividad mayor será el
porcentaje de relaciones fallidas.
La asertividad medida por medio un inventario

17. Correlación nula
 En ella no existe relación entre las dos
variables.

18. Correlación positiva
perfecta
 Es aquella en la que
todos los puntos
están ubicados
exactamente sobre
la línea recta. Y el
coeficiente de
correlación es igual
a 1
0
2
4
6
8
10
12
14
16
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

19. Correlación negativa
perfecta
 Es aquella en la que
todos los puntos
están ubicados
exactamente sobre
la línea recta. Y el
coeficiente de
correlación es igual
a -1
0
2
4
6
8
10
12
14
16
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

20. Correlación de Kendall
 Correlación no paramétrica entre
variables de tipo ordinal y nominal

21. Correlación de Sperarman
 Correlación no paramétrica entre
variables de tipo ordinal y cualquier otra
variable que no se distribuya
normalmente. Siendo la relación ordinal
con nominal, ordinal con ordinal y
ordinal intervalar.

22. Coeficiente de correlación
 Indica en qué medida existe un patrón claro de
alguna relación en particular entre dos
variables. Por ejemplo en el caso de la
correlación positiva particularmente en aquella
en la cual los valores altos coinciden con los
valores altos, el grado de correlación indicará
cuantos valores altos coinciden con otros
valores altos.

23.  Existen coeficientes bajos, medios y
altos.

24. Ejemplo
 Planteamiento del problema
Un profesor desea saber si existe relación
entre el número de horas que sus
alumnos ven televisión y el promedio
general de su materia.
 Variables
 VI: Número de horas que ven televisión los
alumnos
 VD: Promedio general

25. Planteamiento de la
hipótesis
 A mayor número de horas de ver televisión
menor será el promedio general de los
alumnos.
 A menor número de horas de ver televisión
mayor será el promedio general de los
alumnos.

26. Ingreso de datos en el
SPSS

28. SPSS
Analizar
Correlaciones
Bivariada

29. A continuación se despliega el sig. cuadro de diálogo:

30.  Únicamente deben ingresar las
variables que van a correlacionar, elegir
el tipo de correlación (Pearson, Kendall
o Spearman) y dar aceptar.

31. Los resultados se presentan en una tabla como la
siguiente:
Correlación
Edad Número de
hijos
Horas de ver
televisión
Pearson Correlation 1 ,104
Sig. (2-tailed) ,450
N 55 55
Promedio general
Pearson Correlation ,104 1
Sig. (2-tailed) ,450
N 55 55

32. Toma de decisión
 Para la significancia se postulan 2 hipótesis:
 Ho: No existe correlación entre las variables
 HA: Existe correlación entre las variables
 El nivel de significancia es 0.05
 Menor a 0.05 se rechaza Ho.
 Mayor a 0.05 se acepta Ho.

33. Lectura de datos
 El coeficiente de correlación es de 0.104, es
un coeficiente bajo. El nivel de significancia es
de 0.450, al ser mayor a 0.05 se acepta la
hipótesis nula, por lo tanto no existe
correlación entre las variables edad y número
de hijos.