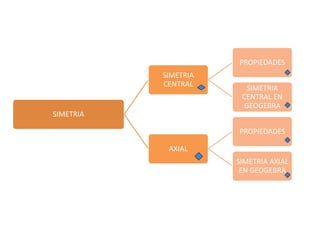
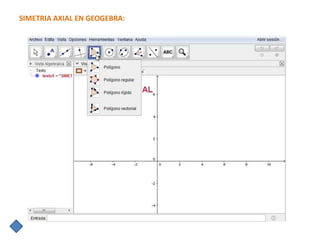
Este documento describe las propiedades de la simetría central y axial. La simetría central hace corresponder puntos a ambos lados de un centro de tal manera que la distancia de cada punto al centro es la misma. La simetría axial hace corresponder puntos a ambos lados de un eje de forma que el segmento que une cada punto con su imagen es perpendicular al eje. El documento explica estas transformaciones geométricas y sus propiedades en GeoGebra.

1. Alum: Mercado, Eugenia Marisa
Prof: Liliana Rios

2. SIMETRIA
SIMETRIA
CENTRAL
PROPIEDADES
SIMETRIA
CENTRAL EN
GEOGEBRA
AXIAL
PROPIEDADES
SIMETRIA AXIAL
EN GEOGEBRA

3. Se llama simetría central a una
transformación geométrica que hace
corresponder a cada punto A del plano otro
punto A’ del plano tales que están alineados
con un punto fijo O, a distinto lado de él y
a la misma distancia AO=OA’
El punto O recibe el nombre de Centro de
simetría.
En una simetría de centro O, A’ es el
homólogo de A y recíprocamente; por lo
tanto, los elementos homólogos en una
simetría central se corresponden
doblemente.
Una figura geométrica tienen centro de simetría cuando sus puntos
son simétricos dos a dos, con relación a O.

4. PROPIEDADES
• El punto, el centro de la simetría y la imagen
pertenecen a una misma recta.
• La imagen y el punto están a una distancia
idéntica de un punto, el cual recibe el nombre de
centro de simetría y es donde se produce el corte de
los dos ejes.
• La imagen de un polígono, mediante simetría
central, es otro polígono congruente con el primero.
• El centro de un cuadrado es centro de simetría
de la figura; de igual manera, el centro de un cubo es
centro de simetría del sólido. El centro de la esfera
lo es también centro de simetría.
DEBE CUMPLIR:

5. SIMETRIA CENTRAL EN GEOGEBRA:

6. Se llama simetría axial a una
transformación geométrica
que hace corresponder a
cada punto A del plano otro
A’ ,tales que la recta que los
une es perpendicular a una
recta fija L de forma que el
segmento AA’ queda
demediado por ella.
La recta L se llama eje de simetría

7. • Todo punto del plano tiene uno y sólo un homólogo
bajo una simetría axial.
Todos los puntos del eje de simetría son homólogos
de sí mismos; se dice que son puntos dobles.
• La simetría axial es una isometría, es decir,
mantiene las distancias.
• Las simetrías axiales transforman los segmentos en
segmentos iguales y las rectas en otras rectas que cortan a
las primeras en puntos M del eje de simetría.
• Las simetrías axiales transforman los ángulos en
otros ángulos iguales pero de sentido contrario.
• Las simetrías axiales transforman una figura en otra
igual o congruente, aunque en sentido inverso.
PROPIEDADES
DEBE CUMPLIR:

8. SIMETRIA AXIAL EN GEOGEBRA: