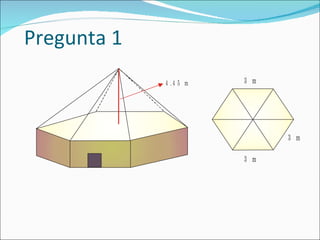
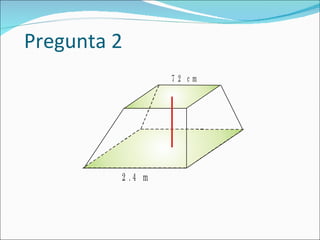
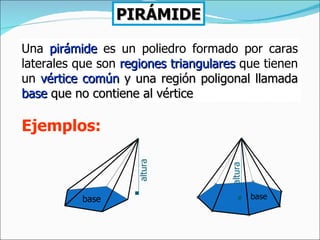
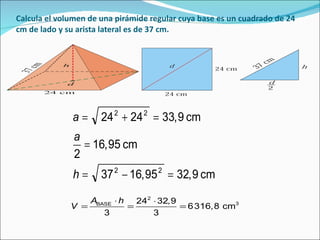
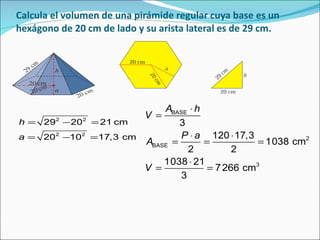
El documento define una pirámide como un poliedro con caras laterales triangulares que comparten un vértice común y una base poligonal. Describe una pirámide regular como aquella con caras laterales isósceles congruentes y aristas laterales congruentes. Explica cómo calcular el área lateral, área total y volumen de una pirámide regular, así como de un tronco de pirámide.

1. PIRÁMIDE Una pirámide es un poliedro formado por caras laterales que son regiones triangulares que tienen un vértice común y una región poligonal llamada base que no contiene al vértice Ejemplos: base base altura altura

2. PIRÁMIDE REGULAR: -Las caras laterales son triangulos isósceles congruentes -Las aristas laterales son congruentes -El apotema (Ap) es la altura relativa a la arista de la base de cualquiera de sus caras laterales Apotema(A p ) Arista lateral (a) altura V A B C D M H Apotema de la base (a b ) Lado de la base (l)

3. AREA LATERAL Si “l” es el lado de la base de la pirámide y A p la apotema de la pirámide A p DE UNA PIRAMIDE REGULAR l

4. AREA TOTAL DE UNA + PIRAMIDE REGULAR a b A p

5. VOLUMEN DE UNA PIRÁMIDE El volumen de una pirámide es igual a un tercio el producto del área de su base por su altura base h V = A base x h 3

6. TRONCO DE PIRÁMIDE Si cortamos una pirámide por un plano, obtenemos un tronco de pirámide, que será recto u oblicuo , según que el plano sea o no paralelo a la base. Fíjate en que las caras laterales de un tronco de pirámide son trapecios y cuando éste es regular, entonces los trapecios son isósceles iguales y su altura coincide con la apotema del tronco de pirámide. Por otra parte, las bases son polígonos semejantes.

7. Pirámides Otros elementos importantes de una pirámide. a a´ APOTEMA LATERAL O ALTURA DE LA CARA ARISTA LATERAL ALTURA DE LA PIRÁMIDE APOTEMA BASE ARISTA BÁSICA BASE

8. Calcula el volumen de una pirámide regular cuya base es un cuadrado de 24 cm de lado y su arista lateral es de 37 cm.

9. Calcular el área lateral, el área total y el volumen de un tronco de pirámide cuadrangular de aristas básicas 24 y 14 cm, y de arista lateral 13 cm.

10. Calcula el volumen de una pirámide regular cuya base es un hexágono de 20 cm de lado y su arista lateral es de 29 cm.

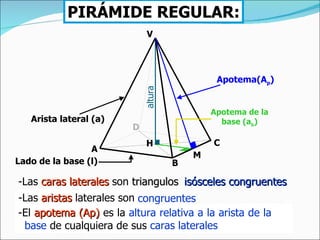
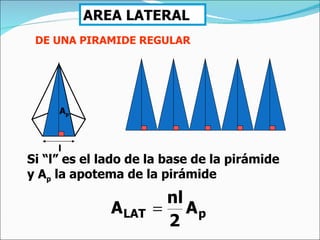
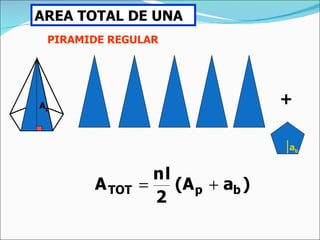
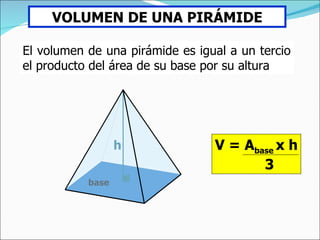
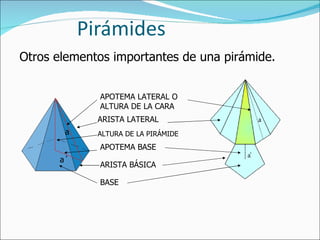
11. EJERCICIO La altura de una pirámide recta de base cuadrada es 4 cm y el lado de la base mide 6 cm. Hallar el área lateral. El área lateral es: Al = P. apo / 2 La apotema es hipotenusa del triángulo rectángulo cuyos catetos son la altura y la mitad del lado de la base. Apo = √ [(l/2) 2 + h 2 )] = √ (3 2 + 4 2 ) = = 5 cm Luego: Al = P. apo / 2 = 4.6.5 / 2 = 60 cm 2 Ejercicios l l h apo l/2

12. Pregunta 1

13. Pregunta 2