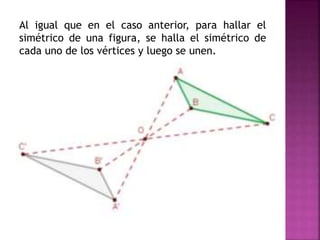
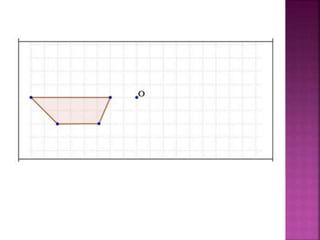
Este documento describe la simetría central y la simetría axial. La simetría central es una rotación de 180° alrededor de un punto central, transformando un punto A en otro punto A' siendo el punto central el medio del segmento AA'. La simetría axial transforma un punto A en A' siendo el eje de simetría la mediatriz del segmento AA'. El documento proporciona instrucciones para encontrar los puntos simétricos y realizar simetrías sobre figuras.

1. • Simetría Central
• Simetría Axial
Prof. Paula Gómez

2. Se trata de un giro de centro
O y de ángulo 180º. También
podemos decir que una
simetría central de centro O
es un movimiento en el
plano que transforma un
punto A en otro A´ siendo O
el punto medio del segmento
AA´.

3.  El simétrico de un punto P respecto de un centro
C es P', si se verifica que: C es el punto medio
del segmento determinado por P y P'.
 Para hallar el simétrico de un punto P, trazamos
la recta que contiene al punto y al centro de
simetría C.
 Haciendo centro con el compás en C, obtenemos
la distancia CP y marcamos con sentido opuesto
el simétrico P’.

4. Al igual que en el caso anterior, para hallar el
simétrico de una figura, se halla el simétrico de
cada uno de los vértices y luego se unen.

6. Dibuja el simétrico de cada figura aplicando la simetría central
de centro al punto dado.

8. Llamamos simetría axial de
eje e a un transformación
mediante la cual se le asocia
a un punto del plano A otro
punto A´, tal que el eje de
simetría e es la mediatriz del
segmento AA´, es decir; la
distancia de A a la recta e es
igual que la distancia del
punto A´a la recta e:
d(A,e)=d(A´,e).

9.  El simétrico de un punto P respecto a un eje
o recta r es P', si se verifica que el eje r es
la mediatriz del segmento determinado por P
y P'.

10.  Para hallar el simétrico de un punto respecto de
un eje, se traza por ese punto una recta
perpendicular al eje y, con centro en la
intersección de la recta y el eje, se toma el
compás con una abertura igual a la distancia del
punto al eje y se corta la recta en el otro
semiplano.
 Para hallar el simétrico de una figura, hallamos
el simétrico de los vértices y luego se unen.

13. Realicen cada una de las siguientes simetrías axiales respecto del eje
marcado en cada caso.