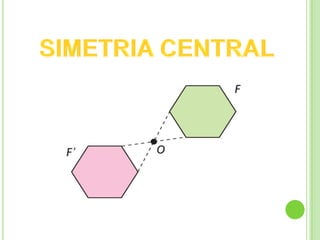
La simetría se refiere a la relación espacial entre figuras, donde puntos corresponden de manera equidistante respecto a un eje, punto o plano. Existen dos tipos principales de simetría: la simetría axial, donde una figura puede ser doblada a lo largo de una línea llamada eje de simetría, y la simetría central, que implica rotación de 180 grados alrededor de un punto central. Se incluyen ejercicios y autoevaluaciones para practicar la identificación de ejes de simetría.

2. La simetría:
Es una relación espacial entre dos figuras, en la que cada
punto se corresponde con otro, de modo que ambos
guardan la misma distancia con respecto a una línea, un
punto o un plano.
En la naturaleza, aunque nada es exactamente simétrico,
podemos encontrar varios casos, como las manos, la cara,
mariposas, pájaros, etc.

3. SIMETRÍA AXIAL:
 Decimos que una figura plana tiene simetría
axial cuando podemos trazar una recta
(llamada eje de simetría) que divida en dos
partes la figura, de manera que si plegamos el
plano por ese eje las dos partes coinciden.
Observa que una parte "se refleja" en el eje
para formar la otra, como si el eje actuase de
espejo.

4.  Ejercicios:
 1. Hallar el simétrico del triángulo respecto al eje
en la siguiente figura:

5.  2. Dados los dos polígonos simétricos, hallar el eje
de simetría que transforma uno en el otro:

6. AUTO EVALUACIÓN:
 http://www.gobiernodecanarias.org/educacion/3/Usr
n/matematicas/Geometria/Actividades/Transformaci
ones/autoevaluaciones/evaluacion_simetria_axial.h
tm

8. SIMETRÍA CENTRAL:
 La simetría central es un caso
particular de simetría rotacional
(cuando el ángulo de rotación es de
180º), es decir, P' se obtiene girando
P 180º alrededor de O.
 Una simetría central, de centro el
punto O, es un movimiento del
plano con el que a cada punto P del
plano le hace corresponder otro

9. Nota: la simetría central a veces se
llama simetría con respecto al origen, porque el
"origen" es el punto central alrededor del que
hay simetría.

10. Ejercicios:
1. Dibuja el rectángulo simétrico del dado respecto al
punto O:

11.  2. En la figura aparece una figura y su
simétrica respecto al punto O, ¿dónde se
encuentra dicho punto?

12. AUTOEVALUACIÓN:
 http://www.gobiernodecanarias.org/educacion/3/Usr
n/matematicas/Geometria/Actividades/Transformaci
ones/autoevaluaciones/Evaluacion_simetria_centra
l.htm