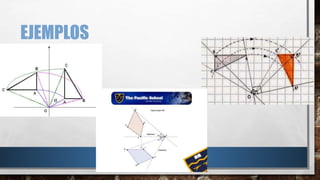
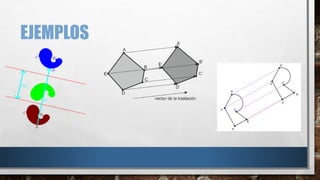
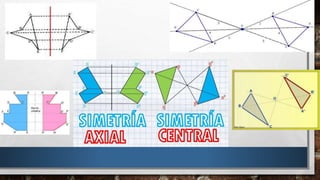
La rotación es una transformación rígida que consiste en girar una figura alrededor de un punto central. Se requieren tres elementos para rotar una figura: el ángulo de giro en grados, el sentido de giro (horario o antihorario), y el centro de rotación. La traslación es el movimiento directo de una figura donde todos sus puntos se mueven en la misma dirección y distancia, manteniendo la forma y tamaño original. La simetría axial ocurre alrededor de un eje, donde los puntos de una figura coinciden