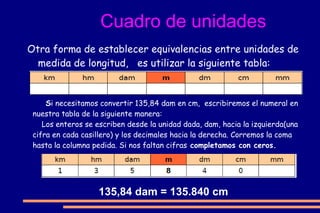
El documento explica el sistema métrico decimal, incluyendo las unidades de longitud (metro y sus múltiplos/submúltiplos), capacidad (litro) y masa (kilogramo). Describe cómo se usan prefijos como kilo y centi para indicar múltiplos y submúltiplos, y cómo convertir entre unidades usando la escalera métrica y tablas de conversión. También cubre mediciones complejas e incomplejas y operaciones con medidas de longitud.

1. SISTEMA MÉTRICO DECIMAL 5º DE PRIMARIA C.E.I.P. TARTESSOS

2. E l sistema métrico decimal • Antiguamente cada país, tenía su propio sistema de unidades y una misma denominación representaba un valor distinto. • Fue implantado por la Primera Conferencia General de Pesos y Medidas (París, 1889). • Su finalidad: establecer un sistema de unidades único para todo el mundo. • Como unidad de medida de longitud se adoptó: el metro. • Como unidad de medida de capacidad se adoptó: el litro. • Como unidad de medida de masa se adoptó: el kilogramo. • Se llama así porque tiene como unidad el metro , y porque cada unidad de un orden es diez veces mayor que la unidad de orden inmediatamente inferior y a la vez la décima parte de la unidad del orden inmediato superior .

3. TODAS LAS UNIDADES DE MEDIDA UTILIZAN UN MISMO CONJUNTO DE PREFIJOS PARA INDICAR CADA MÚLTIPLO O SUBMÚLTIPLO. miria : para 10.000 veces deci : para 0,1 kilo : para 1.000 veces centi : para 0,01 hecto : para 100 veces mili : para 0,001 deca : para 10 veces

4. LAS MEDIDAS DE LONGITUD

5. ¿CÓMO EMPEZÓ EL HOMBRE A MEDIR? • En la antigüedad para medir utilizaban el cuerpo humano. • Ahora en algunos países (Chile, Guatemala, Nicaragua,..) utilizan unidades de medida basadas en partes del cuerpo humano. • Nosotros también podemos medir objetos con nuestro cuerpo.

6. VAMOS A MEDIR CON NUESTRO CUERPO Para medir podemos utilizar distintas partes del cuerpo: • Dedos • Pies • Palmos • Pasos

7. ¿CON QUÉ PODEMOS MEDIR?

8. ¿CÓMO MEDIR SIN EQUIVOCARNOS? Colocamos la regla sobre el objeto , haciendo que coincida el número CERO de la regla con uno de los extremos y se mira el número que coincide en el otro extremo, eso es lo que mide el objeto. El martillo mide 6 centímetros.

9. EL METRO El metro se considera la unidad principal de longitud; su símbolo es: m

10. MÚLTIPLOS DEL METRO Para medir longitudes grandes, utilizamos unidades mayores que el metro, como el kilómetro, el hectómetro y el decámetro; son sus múltiplos:

11. SUBMÚLTIPLOS DEL METRO Para medir longitudes pequeñas, utilizamos unidades menores que el metro, como el decímetro, el centímetro y el milímetro; son sus submúltiplos:

12. Cada unidad de longitud es 10 veces mayor que su inmediata inferior y 10 veces menor que su inmediata superior. Relaciones entre las unidades de longitud

13. ESCALERA DE LAS UNIDADES DE LONGITUD (Pasar de una unidad más grande a otra más pequeña) Para pasar de una unidad más grande a otra más pequeña ,(bajar la escalera)tenemos que multiplicar por un 1 seguido de tantos ceros como escalones haya que bajar.

14. Ejemplo: para pasar de km a m hay que bajar 3 escalones, por lo tanto hay que multiplicar por 1.000.

15. 5km = 5 X 1.000 = 5.000 m

16. ¡No es tan difícil ! Contemos en la escalera anterior los escalones que van desde el Km, hasta el cm, total 5 escalones. Pues multipliquemos los 8 Km por la unidad seguida de cinco ceros, es decir por 100.000. Así : 8 x 100.000 = 800.000 ¿Ves qué fácil? Cuando bajamos la escalera , se multiplica por la unidad seguida de tantos ceros como escalones se bajan, que es lo mismo que añadir al número, esos mismos ceros o correr la coma tantos lugares a la derecha , como escalones hayamos bajado Por tanto en nuestro ejemplo quedaría resuelto así: 8 Km = 800.000 cm Je, je ¿Quién resuelve este problema? : 8 Km = ........ cm

17. ESCALERA DE LAS UNIDADES DE LONGITUD (Pasar de una unidad más pequeña a otra más grande ) Para pasar de una unidad más pequeña a otra más grande ,(subir la escalera) tenemos que dividir por un 1 seguido de tantos ceros como escalones haya que subir.

18. Ejemplo: para pasar de cm a m hay que subir 2 escalones, por lo tanto, hay que dividir por 100.

19. 150 cm =150:100= 1,50 m

20. Tampoco tiene ninguna dificultad : haremos lo mismo, pero al revés : subimos la escalera y contamos los escalones que van desde el dm al hm, en nuestro caso van tres. Pues dividimos los 8 dm por la unidad seguida de tres ceros , así : 8 : 1000 = 0,008 Cosa que tú sabes hacer, porque lo has dado en temas anteriores: separas con una coma a partir del 8 , tantos números como ceros acompañan a la unidad o lo que es lo mismo, escalones hayas contado, tres. Por tanto, ya está solucionado el problema inicial: 8 dm = 0,008 hm ¡MÁS DIFÍCIL TODAVÍA! 8 dm=.........hm

21. Cuadro de unidades Otra forma de establecer equivalencias entre unidades de medida de longitud, es utilizar la siguiente tabla: S i necesitamos convertir 135,84 dam en cm, escribiremos el numeral en nuestra tabla de la siguiente manera: Los enteros se escriben desde la unidad dada, dam, hacia la izquierda(una cifra en cada casillero) y los decimales hacia la derecha. Corremos la coma hasta la columna pedida. Si nos faltan cifras completamos con ceros. 135,84 dam = 135.840 cm

22. VAMOS A PRACTICAR km hm dam m dm cm mm 46,2m 4 6 2 8,35 hm 36,21 dm 0,35 km 0,41 dam 450 mm 462 dm .....m . ....cm ....hm ....m .....dm Copia y completa en tu cuaderno.

23. Expresiones complejas e incomplejas Cuando expresamos una medición utilizando varias unidades, lo hacemos en forma COMPLEJA . Hay muchos ejemplos de ello en la vida ordinaria: 2 Km, 6 hm y 20 m ( Expresa una distancia ) 7 Kg y 200 g ( Expresa un peso ) Cuando expresamos una medición utilizando una sola unidad, lo hacemos en forma INCOMPLEJA . Hay muchos ejemplos de ello en la vida ordinaria: 2 Km (Expresa una distancia ) 200 g ( Expresa un peso ) 3 Euros ( Expresa un precio )