Solsem01

UNMSM-CENTRO PREUNIVERSITARIO
Ciclo 2009-II

UNIVERSIDAD NACIONAL MAYOR DE SAN MARCOS
Universidad del Perú, DECANA DE AMÉRICA
CENTRO PREUNIVERSITARIO

Habilidad Verbal
SEMANA 1 A

LA JERARQUÍA TEXTUAL: EL TEMA CENTRAL

El texto es una cadena de enunciados, pero no todos gozan del mismo estatus. En
todo texto, hay un principio de jerarquía. Este principio sostiene que el texto está
gobernado por una noción capital, el tema central, crucial para entender la trama
textual, puesto que es el concepto más prominente, esto es, de mayor importancia
cognitiva en la estructura semántica del conjunto de enunciados. El tema central se
formula mediante un vocablo o una frase nominal, por ejemplo, «El derecho a la
eutanasia».

ACTIVIDADES DE RECONOCIMIENTO DEL TEMA CENTRAL

A. Formule el tema central del siguiente texto.

TEXTO

Ahora resulta que ver películas del director David Lynch o leer relatos de Franz
Kafka nos puede volver más listos. Un artículo de los psicólogos Travis Proulx, de la
Universidad de California en Santa Bárbara, y Steven J. Heine, de la Universidad de
Columbia, ambas en Estados Unidos, publicado en la revista Psychological Science,
afirma que las obras surrealistas –como el cuento Un médico rural, de Kafka, o la película
Terciopelo azul, de Lynch– pueden hacer que nuestro cerebro se vea obligado a trabajar
‘tiempo extra’ y formar nuevos patrones de pensamiento; esto como respuesta a
estímulos inesperados que perturben la lógica de la realidad. Proulx asevera que “las
personas nos incomodamos cuando las asociaciones que esperamos son transgredidas, y
eso crea un deseo inconsciente de dar urgentemente sentido a lo que nos rodea”. Esa
sensación “nos incita a desarrollar una mayor capacidad de aprendizaje.

Tema central: ________________________________________________________

Solución:
Obras surrealistas y desarrollo de la inteligencia.

B. Lea el texto y conteste la pregunta de opción múltiple.

Semana Nº 01 (Prohibida su reproducción y venta) Pág. 1

Ciclo 2009-II

TEXTO

Un reporte del Institute for Operations Research and the Management Sciences
advirtió que el número de soldados estadounidenses que padecerán trastorno de estrés
postraumático (TEPT) se incrementará en 35%, cálculo alarmante que debe ser tomado
en cuenta por la Asociación de Veteranos de aquel país no solo para analizar las causas
del aumento, sino para enfrentarlo de manera adecuada.
El TEPT es un trastorno psicológico ocasionado por eventos traumáticos, una
secuela de actos de violencia física, accidentes, desastres o combate armado; los
pacientes recuerdan con constancia los episodios que vivieron, sufren insomnio, tienen
pesadillas y se sienten paralizados emocionalmente, incapacitándolos para reincorporarse
a la vida civil. Una de las razones que propiciarían este padecimiento podría ser el
constante despliegue de soldados que se registró en la guerra de Irak, el más elevado
desde la Segunda Guerra Mundial, con períodos breves de descanso para los
combatientes.

1. ¿Cuál es el tema central del texto?

A) El trastorno de estrés postraumático desde las guerras mundiales.
B) El incremento del trastorno de estrés postraumático en el mundo.
C) Trastorno de estrés postraumático en soldados estadounidenses.
D) Efectos emocionales en los trastornos de estrés postraumático.
E) El trauma producido en Irak por el constante despliegue americano.

Solución:
El texto se refiere, centralmente, a un reporte que registra un preocupante aumento
del trastorno de estrés postraumático en los soldados estadounidenses.
Clave: C

LA JERARQUÍA TEXTUAL: LA IDEA PRINCIPAL

Una vez que hemos determinado el tema central de un texto, resulta fácil establecer
la idea principal. Esta se formula mediante una oración o un enunciado. Por ejemplo, si el
tema central de un texto es «El derecho a la eutanasia», la idea principal puede ser «El
derecho a la eutanasia es fundamental en una sociedad civilizada». En consecuencia, la
idea principal es el desarrollo esencial del tema central que se hace en el texto.

ACTIVIDADES DE RECONOCIMIENTO DE LA IDEA PRINCIPAL

A. Formule la idea principal del siguiente texto.

TEXTO

El cambio sucesivo en el tratamiento de los caracteres es un índice muy significativo
del crecimiento de Shakespeare como dramaturgo. En sus obras primeras, los personajes
luchan con las fuerzas externas más que con los problemas subjetivos. En una eximia
tragedia como Romeo y Julieta, el héroe lucha con problemas exteriores más que con él
mismo. En sus grandes tragedias posteriores, el conflicto interior se enfatiza más, como
en Hamlet y en Macbeth. En estas estupendas obras, cada vez más se abandona el
incidente externo a favor de acciones basadas en el error de identidad o en un conflicto
endógeno. Shakespeare muestra su maestría en el análisis del carácter: la maldad en
Macbeth, los celos en Otelo, la indecisión en Hamlet. Así, se incide cada vez más en la

Ciclo 2009-II

exploración de los vanos intentos de los dramatis personae por escapar a las
consecuencias de sus acciones.

Idea principal: ________________________________________________________

Solución:
La complejización de los personajes evidencia la evolución de Shakespeare como
dramaturgo.
B. Lea el texto y conteste la pregunta de opción múltiple.

TEXTO

La palabra ‘dios’ proviene del latín deus. En más de un tratado se sugiere que, a su
vez, este vocablo deriva del griego Zeus, que era la máxima divinidad de aquel magnífico
pueblo de la Antigüedad, cuna de lo que hoy conocemos como civilización occidental. Un
especialista, el profesor Jorge Bosia, señala que tanto el término latino como el griego
tienen su origen idiomático en la cultura indoeuropea, y que la raíz es dya, lo que
emparenta de inmediato la idea de dios con la del día, la luz, lo que enfrenta a las
tinieblas satánicas. Esto encaja a la perfección con las civilizaciones antiguas que, casi en
su totalidad, divinizaban al Sol (como en el caso de Ra, para los egipcios) o las estrellas
(hecho común en la mitología grecorromana). Justamente del Sol es de donde proviene la
luz que ilumina a nuestro planeta. Aunque parezca mentira, lo único que se ha establecido
de la luz es su velocidad: 300 000 kilómetros por segundo. Pero se ignora cómo está
compuesta, pues todo lo que se dice al respecto son meras hipótesis. En una palabra, no
se sabe qué es la luz.
El profesor Bosia tiene su respuesta –bella, poética y llena de fe–: “Yo creo que la
luz es simplemente Dios y que estamos bañados de Él”. Habría que agregar que es una
pena que muy a menudo no nos demos cuenta de esa maravilla, de esa visible
manifestación que la ciencia aún no explica.

1. ¿Cuál es la idea principal del texto?

A) Es un hecho deplorable que los seres humanos sean incapaces de ver la
refulgencia de la luz del día.
B) Dado que para la ciencia la naturaleza de la luz es insondable, se impone una
visión poética llena de fe.
C) Se puede establecer fehacientemente que hay un nexo semántico profundo
entre ‘dios’ y ‘Zeus’.
D) En las civilizaciones antiguas, el culto solar fue una manifestación de la pureza
religiosa más perfecta.
E) Gracias a un análisis etimológico, se puede sostener que la idea de dios está
emparentada con la idea de luz.

Solución:
Medularmente, el texto expone la sugerencia del profesor Bosia, según la cual la
idea de dios está emparentada con la idea de día, la luz.
Clave: E


Ciclo 2009-II

DESARROLLO DE LÉXICO ACROLECTAL

Escriba una oración que desarrolle el significado de los siguientes términos.

1. Abstruso: Recóndito, de difícil comprensión.
2. Abúlico: Falto de voluntad.
3. Acuciante: Apremiante, urgente.
4. Admonición: Advertencia, reprensión.
5. Alevosía: Traición, perfidia.
6. Anuencia: Consentimiento, aprobación.
7. Argucia: Argumento falaz.
8. Asiduo: Que acude con frecuencia y perseverancia.
9. Atónito: Pasmado, asombrado.
10. Atribulado: Sujeto que se siente afligido o acongojado.

COMPRENSIÓN DE TEXTOS

Cuatro clases de objetos circunnavegan el Sol. Los objetos más grandes que dan
vueltas a su alrededor se llaman planetas; los objetos menores abarcan los asteroides, los
cometas y los meteoritos. La palabra planeta viene de una palabra griega que quiere decir
estrella errante. Un planeta es un objeto del espacio que gira alrededor del Sol. No
produce luz propia, pero la luz solar incide en su superficie y se refleja en él. De manera
que un planeta parece brillar en el cielo, porque la luz solar rebota en su superficie.
Hasta el año 2006, se consideraba que nuestro sistema solar tenía nueve planetas.
Sin embargo, la Unión Astronómica Internacional, el 24 de agosto de 2006, ha establecido
que Plutón no es un planeta, debido a su pequeña dimensión y a su carácter bastante
excéntrico respecto del Sol.
Todos los planetas se mueven alrededor del Sol en una órbita elíptica. Los planetas
más próximos al Sol tienen órbitas más cortas que los que están más lejos. Mientras cada
planeta gira alrededor del Sol, también rota o gira sobre sí mismo. Los planetas se han
dividido en dos grupos. Los más próximos al Sol se llaman planetas interiores: Mercurio,
Venus, Tierra y Marte. Los más lejanos del Sol se denominan planetas exteriores: Júpiter,
Saturno, Urano y Neptuno.
Los planetas interiores se parecen a la Tierra en cierto modo. Al igual que la Tierra,
están hechos de rocas y metales. El más grande de los planetas interiores es la Tierra,
que mide 12800 kilómetros de diámetro; el más pequeño es Mercurio con 4990 kilómetros
de diámetro.
Mercurio es un planeta que se mueve rápido: solamente le toma 88 días hacer un
viaje completo alrededor del Sol. Como la Luna, satélite de la Tierra, Mercurio tiene
muchos cráteres. Sin embargo, carece de luna propia y su atmósfera es extremadamente
sutil. Venus es el más brillante de todos los planetas: tiene más fulgor que una estrella. No
obstante, evidentemente, su luz no es propia, es un reflejo del Sol. La atmósfera de Venus
es densa, pues contiene bióxido de carbono y, dado que este gas mantiene el calor
atrapado, la temperatura de Venus siempre supera los 480 grados centígrados. Este
planeta no tiene luna y está cubierto de cráteres, montañas y valles.
La Tierra se llama el “planeta vivo”, por cuanto es el único planeta conocido donde
hay vida. La atmósfera de la Tierra tiene grandes cantidades de oxígeno y vapor de agua
y estos gases ayudan a que la vida sea posible en nuestro globo. Marte es un planeta
rocoso que se ve de color rojo en el espacio. Marte, con dos lunas pequeñas, tiene una
atmósfera tenue y casquetes polares de hielo; asimismo, extensas áreas desérticas rojas
dan al planeta su color.

Ciclo 2009-II

Los planetas exteriores son más grandes que los interiores y están constituidos,
principalmente, de gases. Los científicos creen que los planetas exteriores tienen
atmósferas que contienen grandes cantidades de hidrógeno y helio, además de pequeñas
cantidades de amoníaco y metano congelados. Es posible que el centro de estos planetas
contenga líquidos pesados.
Júpiter es dos veces más grande que todos los demás planetas reunidos: tiene
142700 km de diámetro y 60 lunas giran a su alrededor. Parece tener una enorme zona
roja en su superficie, denominada la Gran Mancha Roja (cabrían allí tres Tierras). Esta
ingente zona parece ser una gigantesca tormenta de gases causada por el ascenso de
nuevos gases desde las profundidades del planeta. Júpiter tiene un tenue sistema de
anillos invisible desde la Tierra. Por otro lado, Saturno es uno de los planetas más
hermosos. Poseedor de 31 satélites y rodeado de siete anillos, se cree que estos anillos
constan de miles de millones de trocitos de roca y hielo que giran alrededor del planeta
como si fueran diminutas lunas.
Urano y Neptuno son llamados los planetas gemelos: se parecen y tienen más o
menos el mismo tamaño. No obstante, Urano tiene nueve anillos y quince lunas; Neptuno
tiene un conjunto de cinco anillos y ocho lunas. Puesto que Neptuno está más alejado del
Sol, es más frío que Urano.
Los objetos menores del sistema son los asteroides, los cometas y los meteoritos.
Mientras que algunos asteroides tienen un kilómetro de diámetro, otros pueden llegar a
los cientos de kilómetros. Los cometas ofrecen una visión espectacular y la gran mayoría
tiene solamente unos kilómetros de diámetro. El más famoso es el cometa Halley que
pasó cerca de la Tierra en 1986 y volverá a pasar en el 2061. Los meteoritos, por otro
lado, son objetos de roca y metal que vuelan a toda velocidad alrededor del Sol. La
mayoría de meteoritos se disgrega al rozar la Tierra, pero si un meteorito logra entrar en
la atmósfera terrestre, podría causar un impacto considerable (por ejemplo, un cráter de
un kilómetro de ancho).

1. En el texto, el término SUTIL significa

A) profunda. B) tenue. C) lúcida. D) frágil. E) sofisticada.

Solución:
Cuando se habla de una atmósfera extremadamente sutil se quiere decir que es
tenue (delgada).
Clave: B

2. La serie de cohipónimos más coherente es

A) Mercurio, Venus, Tierra.
D) Plutón, Júpiter, Saturno
B) Urano, Neptuno, Marte.
E) Sol, estrella, asteroide.
C) Anillo, cometa, meteorito.

Solución:
Dado que son planetas interiores, esto es, más cercanos al Sol.
Clave: A


Ciclo 2009-II

3. ¿Cuál es el tema central?

A) El Sol y los planetas del sistema planetario.
B) Cuatro tipo de objetos del sistema solar.
C) Los planetas del espacio y sus satélites.
D) Planetas interiores, cometas y asteroides.
E) Planetas interiores y planetas exteriores.

Solución:
El texto se centra en los objetos del sistema solar: planetas, asteroides, cometas y
meteoritos.
Clave: B
4. ¿Cuál es el mejor resumen del texto?

A) Nuestro sistema solar se define por tener ocho planetas que se mueven
alrededor del Sol; algunos son considerados interiores y los más grandes son
considerados exteriores; casi todos poseen varias lunas.
B) Los objetos que se pueden encontrar en el sistema solar son los planetas,
asteroides, cometas y meteoritos; los planetas tanto interiores como exteriores
se caracterizan por su mayor dimensión y su órbita elíptica.
C) Los objetos que abundan en el universo y que son descritos por los astrónomos
se caracterizan por carecer de brillo propio, dado que su luz se origina en un
reflejo a partir de la materia y energía del cuerpo solar.
D) Todos los planetas que hay en el universo sideral se dividen en dos grupos: los
interiores, porque están muy próximos al cuerpo solar; los exteriores, debido a
que se hallan en los confines últimos de la galaxia estelar.
E) Por mucho tiempo se pensó que los planetas del sistema solar eran nueve
objetos hasta que, en el año de 2006, la Unión Astronómica Internacional
determinó que Plutón, por su dimensión, no era un planeta verdadero.

Solución:
El resumen expande el tema central referido a los cuatro tipos de objetos que se
hallan en nuestro sistema solar.
Clave: B
5. ¿Cuál es la secuencia que desarrolla la estructura temática del texto?

A) Planetas del sistema solar, planetas interiores, planetas exteriores, asteroides,
cometas y meteoritos.
B) El sistema galáctico, la estructura del Sol, planetas del sistema solar, colisiones
de meteoritos.
C) Noción helénica de planeta, estructura del sistema solar, dimensión de los
objetos del espacio.
D) Visibilidad de los planetas, dimensión de los planetas, diferencia entre asteroides
y meteoritos.
E) Estructura del Sol, planetas del sistema solar, satélites de los planetas,
diversidad de asteroides.

Solución:
Se trata de la secuencia expositiva que desarrolla los cuatro tipos de objetos del
sistema solar.
Clave: A

Ciclo 2009-II

6. ¿Cuál de las siguientes características no es necesaria para que un objeto sea
considerado un planeta?

A) Moverse elípticamente. B) Rotar sobre su eje.
C) Reflejar la luz solar. D) Tener al menos un satélite.
E) Tener órbita circunsolar.

Solución:
Hay planetas que no tienen satélites.
Clave: D
7. El planeta interior se define por

A) estar más próximo al cuerpo solar.
B) ser más pequeño que un asteroide.
C) tener la misma dimensión de Plutón.
D) poseer más de un satélite.
E) seguir una órbita circular.

Solución:
El planeta interior se caracteriza por su mayor cercanía al Sol, lo que se establece
nítidamente al efectuar la comparación con los planetas llamados exteriores.
Clave: A

8. Determine la verdad (V) o la falsedad (F) de los siguientes enunciados en función del
contenido del texto.

I. Hacia el año 2000 Plutón todavía era considerado como un planeta más.
II. El cometa Halley se mueve con una órbita circunsolar de ochenta años.
III. Todos los cráteres terrestres se explican por el impacto de meteoritos.
IV. Los meteoritos se caracterizan por tener un movimiento muy raudo.
V. Todos los planetas llamados exteriores tienen satélites a su alrededor.
VI. Los asteroides suelen ser mucho más pequeños que los meteoritos.

A) FFFFVV B) VVVVFF C) VFFVVF D) FFFVVV E) VVFVVF

Solución:
Son los apropiados valores de verdad de acuerdo con el contenido expuesto a lo
largo del texto.
Clave: C

9. Si un objeto tuviera 700 kilómetros de diámetro,

A) se consideraría un planeta pequeño. B) podría ser un asteroide grande.
C) sólo podría ser como un cometa. D) sería un planeta llamado interior.
E) sería como un satélite de Mercurio.

Solución:
En virtud de esa dimensión, calzaría en la definición de asteroide.
Clave: B


Ciclo 2009-II

10. Si Plutón tuviera cinco mil kilómetros de diámetro,

A) sería más pequeño que el planeta Mercurio.
B) podría ser considerado como un asteroide.
C) varios satélites girarían en torno de aquél.
D) debería denominarse como planeta interior.
E) el sistema solar contaría con nueve planetas.

Solución:
Plutón ha dejado de ser considerado un planeta por su exigua dimensión. Si tuviera
ese diámetro, seguiría siendo considerado un planeta.
Clave: E

SEMANA 1 B

ELIMINACIÓN DE ORACIONES

Los ejercicios de eliminación de oraciones establecen dos criterios sobre el manejo de
la información en un texto determinado: a) La cohesión temática y b) la economía de la
expresión. En virtud de estos criterios, la eliminación de oraciones se puede hacer de dos
maneras alternativas: a) O bien se suprime la oración que no corresponde al tema clave
del conjunto; b) o bien se suprime la oración redundante, esto es, la que no aporta
información al conjunto.

1. I) El cómic es un género narrativo moderno constituido por representaciones
gráficas. II) En él, el relato de la acción se da mediante una secuencia de cuadros o
viñetas. III) Cada viñeta se compone de imágenes frecuentemente acompañadas de
textos. IV) Todo género narrativo requiere de un inicio, desarrollo y desenlace.
V) Con el fin de conservar la fluidez de la narración, cada viñeta debe conducir
visualmente a la siguiente.

A) II B) III C) I D) IV E) V

Solución:
El tema es el cómic. Resulta no atingente dilucidar algo referido a todo género
narrativo, por su generalidad.
Clave: D

2. I) A diferencia de los insectos, que tienen seis patas, las arañas tienen ocho. II) No
tienen alas ni antenas, sino un par de palpos delgados a ambos lados de la cabeza
que pueden parecer antenas. III) Las arañas no son insectos, son arácnidos. IV) Las
arañas son arácnidos capaces de producir hilo, con el que pueden tejer una telaraña
en la que atrapan a sus presas. V) Son hábiles cazadoras y cuentan con colmillos
venenosos con los cuales paralizan a sus presas para devorarlas.

A) V B) I C) IV D) II E) III

Solución:
Enunciado claramente redundante o superfluo.


Ciclo 2009-II

3. I) New York posee la concentración urbana más grande de nuestro globo. II) Está
formada por cinco condados o grandes barrios. III) La ciudad de New York es la más
poblada del mundo y cuenta con la actividad más intensa y más gravitante de los
Estados Unidos. IV) Es, asimismo, un gran centro cosmopolita, que agrupa las más
diversas razas y nacionalidades. V) La edificación neoyorquina es colosal, con sus
típicos e impresionantes rascacielos.

A) I B) V C) III D) IV E) II

Solución:
Enunciado nítidamente redundante.
Clave: A
4. I) Jack Parsons fue investigador del Instituto Tecnológico de California, y uno de los
tres fundadores del Jet Propulsion Laboratory. II) Jack Parsons fue seguidor de la
magia negra y discípulo del ocultista inglés Aleister Crowley. III) Es, además, pionero
en el desarrollo del combustible sólido para cohetes. IV) Sus investigaciones
ayudaron a realizar los viajes espaciales modernos. V) Jack Parsons murió en su
laboratorio casero por las heridas que le ocasionó la explosión de un experimento
con fulminato de mercurio.

A) V B) I C) III D) II E) IV

Solución:
Enunciado inatingente, dado que no se refiere a la dimensión tecnológica de
Parsons.
Clave: D

5. I) La corteza cerebral es una capa de tejido neural que cubre gran parte del cerebro.
II) En contraste con el sistema serotonérgico, la neocorteza, una parte de la corteza
cerebral, es una estructura presente solo en los mamíferos. III) El tamaño de la
neocorteza está relacionado fundamentalmente con la masa corporal. IV) La
neocorteza es una capa plegada de tejido neural de un par de milímetros de grosor.
V) Una propiedad fundamental de la neocorteza es que contiene mapas
topográficos.

A) II B) V C) I D) IV E) III

Solución:
Enunciado inatingente, pues el conjunto está referido a la neocorteza.
Clave: C

6. I) La teoría einsteiniana de la relatividad general se basa en la sugerencia
revolucionaria de que la gravedad no es una fuerza, sino una consecuencia de que
el espacio tiempo no es plano. II) En la relatividad general, el espacio tiempo está
curvado por la distribución de masa y energía que contiene. III) Según la teoría, los
objetos no se mueven en órbitas curvadas a causa de una fuerza llamada gravedad,
sino porque siguen una trayectoria lo más próxima posible a una línea recta en un
espacio curvado: una geodésica. IV) El postulado fundamental de la relatividad
especial establece que las leyes deberían ser las mismas para todos los
observadores que se mueven libremente. V) En la relatividad general, el tiempo
transcurre de forma diferente para observadores en campos gravitatorios diferentes.

Ciclo 2009-II

A) II B) IV C) III D) V E) I

Solución:
Se elimina por no pertinencia: el tema es la relatividad general, no la relatividad
especial.
Clave: B

7. I) En la mitología helénica, el Minotauro es una criatura monstruosa con cuerpo de
hombre y cabeza de toro, nacido de Pasifae –mujer de Minos– y de un toro blanco.
II) El monstruo residía en un laberinto diseñado especialmente por el gran arquitecto
Dédalo. III) La monstruosa criatura se alimentaba de carne humana, en especial de
jóvenes griegos. IV) En el código psicoanalítico, el Minotauro simboliza la virilidad y
la inusitada fuerza física. V) Según la tradición mítica griega, el Minotauro fue muerto
por el egregio héroe Teseo, ayudado por Ariadna.

A) V B) II C) IV D) I E) III

Solución:
Se elimina por no pertinencia: el tema es el mito helénico del Minotauro, no su valor
simbólico dentro del psicoanálisis contemporáneo.
Clave: C

8. I) El método usado en las ciencias se rige por una tríada esencial: problema,
hipótesis, contrastación. II) En las llamadas ciencias naturales, el método ha
mostrado su éxito, aunque suele haber discusiones sobre su correcta definición.
III) Bacon y Descartes propusieron un método científico para llegar a la verdad en
las ciencias. IV) Según Bacon, el método científico utiliza un conjunto de reglas
inductivas para llegar al conocimiento científico. V) Para Descartes, el método
científico utiliza la deducción y la intuición para arribar a la certeza científica.

A) III B) V C) II D) IV E) I

Solución:
Se elimina por redundancia: el contenido de la oración III está implicado en IV y V.
Clave: A

COMPRENSIÓN DE LECTURA

Hace miles de años, el sabio rey Salomón reparó en la hormiga, en su gran espíritu
de colaboración, y nos la puso como un modelo digno de imitar. En efecto, las hormigas
son un mirífico ejemplo de colaboración, laboriosidad y orden: suelen aunar esfuerzos
para arrastrar hasta su hogar objetos mucho más grandes que ellas. El paradigmático
caso de las hormigas revela que, en la naturaleza, la supervivencia estriba tanto en la
interrelación con los vecinos como en el crecimiento y la reproducción.
Cuanto más conocemos los secretos del universo, más nos asombran la
interdependencia y la armonía existentes en el mundo que nos rodea. Como en una
perfecta orquesta, todos los organismos ejercitan su parte en la interpretación de la
deliciosa sinfonía de la vida.
Si nos dirigimos a las llanuras de África, veremos que impalas y babuinos suelen
trabajar juntos. Con el agudo olfato del impala y la excelente vista del simio, difícilmente
se acercará algún depredador sin ser detectado. Lo mismo se da entre los rumiantes, esto


Ciclo 2009-II

es, las criaturas que, como las vacas, venados y ovejas, vuelven a masticar la comida
ingerida. En su rumen (primera cavidad de las varias que constituyen su estómago)
encontramos auténticos ecosistemas de bacterias, hongos y protozoos. Gracias a la
fermentación, estos microorganismos descomponen la celulosa (carbohidrato fibroso de la
vegetación) y la transforman en nutrientes. Asimismo, muchas leguminosas, como la
alfalfa, el trébol y la arveja, mantienen una relación especial con las bacterias, a las que
permiten ‘infectar’ su sistema de raíces; pero las bacterias no las perjudican, sino que
estimulan la producción en las raíces de unos pequeños nódulos donde ellas pueden
instalarse y hacerse cuarenta veces más grandes. De esta forma se convierten en
bacteroides cuya función es transformar el nitrógeno en compuestos asimilables por las
leguminosas. A cambio, las bacterias reciben nutrientes de las plantas.
La cooperación estrecha entre organismos dispares recibe el nombre de simbiosis
que significa, literalmente, convivencia. Hay tres categorías principales de simbiosis:
mutualismo (si la unión resulta provechosa para ambos simbiontes), comensalismo (si
beneficia al huésped sin perjudicar al anfitrión) y parasitismo (si permite a un integrante
medrar a costa del otro).
En general, se entiende por parásito a todo depredador muy especializado cuya
acción sobre el hospedador no provoca la muerte de éste, al menos no inmediatamente.
Al parásito especializado no le conviene producir un daño que pueda acarrear la muerte
de su hospedador, pues la supervivencia de aquél depende de la viabilidad de éste.
Cuando el parásito no resulta tóxico para el hospedador, se pueden establecer relaciones
estables que desencadenan un endoparasitismo permanente. De esta manera, el intestino
de los tiburones suele estar lleno de gusanos parásitos. Los parásitos externos o
ectoparásitos se especializan en muy diferentes acciones: pueden ser hematófagos –se
alimentan de la sangre de otros animales–, dermatófagos –se nutren de la piel–, etc.
Cabe mencionar, como ejemplos de ectoparásitos, a los piojos, las garrapatas y las
pulgas.
En el mutualismo, la explotación de los recursos es mutua, mientras que en el
parasitismo, salvo en contadas ocasiones, el parásito es el único que sale beneficiado y
de manera unilateral aprovecha los recursos del hospedador. Además, el parásito suele
ocasionar una molestia o daño en el otro organismo. Ahora bien, al contrario de lo que
ocurre en el parasitismo, en el mutualismo el hospedador también obtiene beneficios de la
unión con la otra especie. Por ejemplo, en las comunidades de herbívoros que se
alimentan de plantas cuyo componente principal es la celulosa, la existencia de bacterias
simbiontes en su tracto digestivo les reporta grandes cantidades de nutrientes. Existen
simbiontes en los insectos xilófagos (quienes se alimentan de madera) y en los que
ingieren savia u homópteros.
Los arrecifes coralinos están formados por pólipos y algas. Incrustadas en cada
hueco del tejido de los pólipos, las algas aportan al coral sus brillantes colores. Pero la
función principal de las algas es sintetizar compuestos orgánicos, un 98% de los cuales
pagan como una ‘renta’ a su anfitrión. De estos nutrientes dependen los pólipos para vivir
y para formar los esqueletos calcáreos del arrecife. Esta alianza reporta a las algas al
menos dos beneficios: Primero, les proporciona comida. Segundo, les brinda la protección
de un esqueleto resistente.
El mecanismo de la ayuda mutua o simbiosis es vital para la supervivencia de todos
los organismos terrestres y es un mecanismo esencial para diversas formas de vida: si
observas con cuidado en tu jardín, te percatarás de la omnipresencia de la simbiosis.
También ha sido muy importante para el mismo origen de la vida en nuestro globo. Por
esta razón, la bióloga Lynn Margulis ha propuesto un nuevo nombre para la Tierra:
planeta simbiótico.


Ciclo 2009-II

1. El sentido de la palabra MIRÍFICO es

A) prolífico. B) sorprendente. C) magnífico.
D) complicado. E) ubérrimo.

Solución:
Un mirífico ejemplo se entiende como un ejemplo magnífico, formidable.
Clave: C
2. La palabra PERFECTA tiene el sentido preciso de

A) completa. B) compacta. C) integral. D) pasada. E) afiatada.

Solución:
Una perfecta orquesta alude a una orquesta afiatada, con armonía.
Clave: E


A) El mundo natural y el factor evolutivo en la cadena de los seres.
B) La simbiosis como mecanismo de ayuda en el mundo animal.
C) El parasitismo y los más profundos secretos del universo.
D) Las similitudes entre comensalismo, parasitismo y simbiosis.
E) Las diferentes formas de lucha por la vida en la naturaleza.

Solución:
El texto se centra en la simbiosis como un mecanismo nítido de cooperación
interespecies.
Clave: B


A) En el parasitismo, el parásito está muy interesado en colaborar con el hospedero.
B) La simbiosis se puede dar en la forma de mutualismo y en la forma de
parasitismo.
C) El mutualismo acaece cuando un individuo beneficia a otro de la misma especie.
D) La ayuda mutua entre especies es un mecanismo esencial para la vida en la
Tierra.
E) En la naturaleza, hay una lucha encarnizada que también puede mostrarse sutil.

Solución:
Se pone de relieve la ayuda mutua como un mecanismo crucial de colaboración
interespecies.
Clave: D
5. ¿Cuál es el mejor resumen del texto?

A) Desde antiguo, tal como lo atestigua la cita del rey Salomón, se ha logrado ver
con claridad la esencia de la cooperación; en efecto, ningún organismo es una
isla biológica, las especies se relacionan de manera directa o indirecta.
B) En el rumen de una vaca, por ejemplo, se alberga todo un ecosistema de
bacterias, hongos y protozoos; ese caso revela la fuerza de la simbiosis para
establecer el verdadero sentido de la vida en todo el universo natural.

Ciclo 2009-II

C) Para la supervivencia de los seres en la Tierra, el mecanismo simbiótico es
crucial; mientras que el mutualismo entraña una ayuda recíproca, el parasitismo
generalmente implica el beneficio del parásito a expensas del hospedero.
D) Cuando se enfrentan a peligros graves e inminentes, las especies intentan
establecer relaciones dinámicas que buscan establecer mecanismos de alerta
mutua con el objetivo de garantizar la supervivencia de las especies.
E) En la naturaleza, la eterna lucha por la vida se puede expresar, ocasionalmente,
como una manera armónica de complementariedad entre especies diferentes
que suelen vivir en un entorno biológicamente complejo.
Solución:
El texto destaca la simbiosis y presenta sus clásicas dos formas: el mutualismo y el
parasitismo.
Clave: C

6. De acuerdo con el texto, la cooperación entre las hormigas

A) es una forma aguda de parasitismo.
B) no es un ejemplo de relación simbiótica.
C) es un tipo nítido de ectoparasitismo.
D) no tiene importancia para la especie.
E) es un hecho muy insólito en la naturaleza.

Solución:
La relación simbiótica es interespecífica; en consecuencia, la cooperación
intraespecífica no sería un caso de simbiosis.
Clave: B

7. El caso de los arrecifes coralinos, los pólipos y las algas se menciona para poner de
relieve la noción de

A) ectoparasitismo. B) comensalismo. C) imitación.
D) simbiosis. E) ecosistema.

Solución:
Son casos de ayuda mutua entre especies diferentes: ergo, son modalidades de
simbiosis.
Clave: D

8. Si un niño tiene piojos en la cabeza y ello le produce alguna debilidad, estamos
frente a un caso de

A) mutualismo, ya que el piojo recibe un gran beneficio.
B) endoparasitismo, dado que el piojo es muy diminuto.
C) ectoparasitismo que implica un tipo de hematofagia.
D) simbiosis, pues el niño se hará más fuerte con el tiempo.
E) ayuda mutua benéfica para los dos seres involucrados.

Solución:
Dado que los piojos no se encuentran dentro del organismo, se trata de un caso de
ectoparasitismo. Los piojos succionan la sangre: practican la hematofagia.
Clave: C

Ciclo 2009-II

9. Hay mutualismo entre dos organismos cuando

A) el primero beneficia al segundo y éste ayuda a aquél.
B) los dos organismos pertenecen a la misma especie.
C) uno de los organismos puede considerarse depredador.
D) por lo menos, un organismo recibe grandes beneficios.
E) uno de los seres tiene una muerte que es inevitable.

Solución:
Como su nombre lo indica, el mutualismo entraña ayuda recíproca, mutua.
Clave: A

10. En los tejidos de ciertos moluscos hay abundantes trematodos que viven a costa de
los moluscos. Si los moluscos reciben un cierto daño por parte de estos trematodos,
se trata de un caso de

A) ectoparasitismo. B) endoparasitismo. C) mutualismo.
D) comensalismo. E) adaptacionismo.

Solución:
Dado que el beneficio es unilateral y hay daño para un organismo, estamos ante un
caso de endoparasitismo (porque los trematodos viven dentro de los moluscos).
Clave: B

11. La simbiosis entendida como ayuda mutua implica, fundamentalmente,

A) reciprocidad. B) favoritismo. C) causalidad.
D) extinción. E) parasitismo.

Solución:
La ayuda mutua implica un beneficio de los dos organismos: se trata de una acción
recíproca.
Clave: A

12. Determine el valor de verdad (V o F) de los siguientes enunciados, según el
contenido del texto.

I. Los babuinos pueden oler a un depredador a una gran distancia.
II. Los parásitos buscan eliminar al hospedero inmediatamente.
III. Hay un notorio ectoparasitismo entre impalas y babuinos.
IV. Los arrecifes coralinos tienen colores vistosos por las algas.
V. En algunas ocasiones, el hospedero se beneficia del parásito.
VI. Los insectos xilófagos entran en simbiosis con los árboles.

A) VFVFVV B) FFVVVV C) VVVFFF D) FFVFVV E) FFFVVV

Solución:
En virtud del contenido del texto, los tres primeros enunciados son falsos y los tres
últimos enunciados son verdaderos.
Clave: E

Ciclo 2009-II

SEMANA 1 C

SERIES VERBALES

Las palabras no están en nuestra mente como unidades aisladas. Más bien, se
puede sostener con plausibilidad que los vocablos presentan ciertos engarces semánticos
claramente definidos. En el lexicón mental, los vocablos se encuentran reunidos en virtud
de ciertas leyes semánticas de asociación. La noción de serie verbal intenta recoger la
idea de que las palabras no se reúnen por simple yuxtaposición, sino que se organizan en
función de relaciones semánticas definidas.
Ahora bien, las asociaciones léxicas subtendidas por las series verbales son de
variada índole: sinonimia, afinidad, hiperonimia, meronimia, etc. En consecuencia, los
ítems de series verbales son versátiles y plasman la creatividad inherente al lenguaje
humano.

1. Eterno, perenne, imperecedero,

A) precario. B) inmarcesible. C) etéreo.
D) raudo. E) estático.

Solución:
Serie de sinónimos basada en la idea de eternidad.
Clave: B

2. Fulgurante, brillante, esplendente,

A) silente. B) lacerante. C) radiante.
D) turgente. E) detonante.

Solución:
Serie de sinónimos basada en la idea de refulgencia.
Clave: C

3. Vasija, cántaro, garrafa,

A) navío. B) cantera. C) cartabón.
D) fragancia. E) odre.

Solución:
Serie de cohipónimos: recipientes.
Clave: E

4. Boda, casamiento, matrimonio,

A) ágape. B) júbilo. C) remanso.
D) ceremonia. E) himeneo.

Solución:
Serie de palabras afines en torno a los desposorios.
Clave: E

Ciclo 2009-II

5. Cerro, colina, monte,

A) cayo. B) otero. C) bosque.
D) dédalo. E) sima.

Solución:
Serie de cohipónimos.
Clave: B
6. Cola, pegamento, engrudo,

A) gluten. B) escarcha. C) masato.
D) cartulina. E) ungüento.

Solución:
Serie de cohipónimos.
Clave: A

7. Insano, demente, lunático,

A) orate. B) crápula. C) gárrulo.
D) sátiro. E) abstruso.

Solución:
Serie de sinónimos centrada en la idea de locura.
Clave: A

8. Atleta, gimnasio; médico, nosocomio; sacerdote, capellanía;

A) avión, hangar. B) árbol, arboleda.
C) marqués, nobleza. D) fetiche, idolatría.
E) obrero, usina.

Solución:
Serie verbal analógica centrada en la relación de agente-lugar. La serie se proyecta
coherentemente en el par obrero-usina (fábrica).
Clave: E

9. Determine el hiperónimo de la siguiente serie verbal.

A) Parricida B) Uxoricida C) Homicida
D) Filicida E) Magnicida.

Solución:
‘Homicida’ es el término genérico porque está conformado por homi- (hombre,
persona) y de –cida (que mata a). Es, por lo tanto, el hiperónimo de los cuatro
vocablos restantes.
Clave: C


Ciclo 2009-II

10. Pigmeo, liliputiense, enano,

A) dolicocéfalo. B) meridiano. C) arlequín.
D) demonio. E) gnomo.

Solución:
Serie de términos afines en torno a la dimensión diminuta.
Clave: E

11. Calle, vereda; puerta, cerradura; avión, hélice;

A) carnada, anzuelo. B) lápida, cadáver. C) buque, babor.
D) piano, partitura. E) diente, alveolo.

Solución:
Serie verbal fundada en una relación holonímica (todo-parte). Se completa
coherentemente con el par buque, babor.
Clave: C

12. Taco, calzado; tallo, planta; capitel, columna;

A) tortuga, caparazón. B) coágulo, sangre. C) yelmo, visera.
D) cuerda, laúd. E) látigo, azote.

Solución:
Serie verbal fundada en una relación meronímica (parte-todo). Se completa
coherentemente con el par cuerda-laúd.
Clave: D

13. Licaón, chacal, lobo,

A) coyote. B) ocelote. C) leopardo.
D) licántropo. E) nictálope.

Solución:
Serie verbal de cohipónimos.
Clave: A

14. Generosidad, altruismo, filantropía,

A) hermosura. B) esbeltez. C) plétora.
D) limpidez. E) munificencia.

Solución:
Serie verbal de sinónimos centrada en la idea de generosidad.
Clave: E


Ciclo 2009-II

15. Imponente, majestuoso, grave,

A) indemne. B) rayano. C) solemne.
D) austero. E) peregrino.

Solución:
Serie verbal de sinónimos centrada en la idea de gravedad en el trato y la
expresión.
Clave: C

16. Determine el hiperónimo de la siguiente serie verbal.

A) Deducción. B) Abducción. C) Inducción.
D) Analogía. E) Razonamiento.
Solución:
El razonamiento es el término mayor, por cuanto incluye semánticamente a los
demás.
Clave: E

17. Copiosidad, exuberancia, abundancia,

A) plétora. B) boato. C) difusión.
D) turgencia. E) desarrollo.

Solución:
Serie verbal sinonímica basada en la idea de abundancia.
Clave: A

18. Claudicar, renunciar, abandonar,

A) consentir. B) dirimir. C) refutar.
D) abdicar. E) abrogar.

Solución:
Serie verbal basada en la idea de renuncia a un cargo.
Clave: D

COMPRENSIÓN DE LECTURA

TEXTO 1

Muchos consideran que el estrés es una sobrecarga de trabajo y de problemas. En
la oficina, en casa, en nuestra vida social y sentimental, estamos sometidos a emociones,
presiones y tensiones. Estas tensiones crean inestabilidad, lo cual trae consecuencias
sobre nuestra salud física y mental. Para muchas personas es normal padecer de estrés.
A veces, incluso, es motivo de orgullo, un signo de éxito profesional en una sociedad que
nos empuja a ser cada vez más competitivos. En general, el estrés es un estado de
tensión en que se halla una persona, debido a la amenaza de las condiciones
ambientales. Esto ocasiona desequilibrio, baja estima y sentimientos de culpa. Sin
embargo, el estrés no puede considerarse como una enfermedad. Es una respuesta física
y mental del ser humano a los diversos acontecimientos vitales.

Ciclo 2009-II

Hay dos tipos de estrés: psicológico y físico. En el estrés psicológico, las tensiones
mentales se manifiestan a través de una perturbación de los pensamientos. La persona
hace todo deprisa, no piensa antes de actuar, tiene pensamientos obsesivos y se
desconcentra. El cuerpo afectado llega a un estado de desequilibrio que impide regular
correctamente sus funciones. La digestión, el sueño, la respiración y la regulación
cardíaca se ven afectados. La persona manifiesta depresión, hipersensibilidad, ansiedad,
miedo. El estrés físico se manifiesta en tensión de los músculos. Esta tensión aumenta el
nivel del cuello y de los hombros, principalmente el músculo trapecio (músculo del estrés)
y el esternocleidomastoideo. Los músculos maxilares, oculares, de las sienes, de la frente
y de los labios se ven afectados.
El estrés afecta a un 80% de la población mundial. Si conociéramos los desastrosos
efectos del estrés sobre el organismo y la mente, no nos sentiríamos orgullosos ni
encontraríamos normal estar estresado.


A) La tensión muscular y la dolencia ósea como síntomas del estrés.
B) Las marcadas diferencias entre el estrés psicológico y el estrés físico.
C) El estrés como una tensión anormal frente a un entorno problemático.
D) El entrés considerado como la enfermedad más aguda de nuestra vida.
E) Las asombrosas similitudes entre el estrés físico y el estrés psicológico.

Solución:
El tema central es el estrés: una anomalía orgánica o mental motivada por un
entorno tensionante.
Clave: C


A) El estrés es un padecimiento normal, que se explica por el vertiginoso ritmo de la
vida moderna.
B) El estrés psicológico implica pensamientos perturbados que acarrean dolencias
de naturaleza física.
C) El estrés es una gravísima enfermedad contemporánea que afecta a un 80% de
la población mundial.
D) Generalmente, una persona estresada presenta desequilibrio, baja autoestima y
sentimientos de culpa.
E) El estrés es un estado de tensión mental o físico como consecuencia de un
entorno amenazante.

Solución:
La idea central se vincula con la definición del estrés: la tensión mental o física
debido a la amenaza de las condiciones del entorno.
Clave: E

3. Considerar que el estrés es solamente una sobrecarga de trabajo y de graves
responsabilidades es, de acuerdo con el texto,
A) un hecho irrefragable. B) una opinión infundada.
C) una conjetura razonable. D) una deducción científica.
E) una idea excepcional.


Ciclo 2009-II

Solución:
El estrés es anómalo y no ver esto es un error.
Clave: B

4. Se puede establecer una sinonimia entre estrés y

A) emoción. B) tensión. E) cansancio.
D) trabajo. E) entorno.

Solución:
El estrés radica en la tensión (mental o física).
Clave: B

6. Tanto el estrés físico como el estrés psicológico se pueden describir como

A) afecciones gravísimas que padece el ser humano en crecimiento.
B) tensiones mentales que producen alteraciones en el organismo.
C) respuestas adecuadas frente a una situación algo inesperada.
D) estados de tensión que sufren las personas con algún agobio.
E) efectos desastrosos que pueden sobrevenir en el fallecimiento.

Solución:
La condición definitoria del estrés es la tensión producida por un entorno agobiante.
Clave: D

7. En el texto se establece una relación de causa-efecto entre

A) estrés psicológico y movimientos ralentizados.
B) depresión constante y sensación de pánico.
C) una baja estima y fuertes sentimientos de culpa.
D) estrés físico y tensión en el músculo trapecio.
E) sobrecarga de trabajo y sensación de bienestar.

Solución:
Un efecto distintivo del estrés físico es la tensión muscular (en particular, del
trapecio, considerado el músculo del estrés).
Clave: D

8. La intención fundamental del autor es

A) establecer una distinción entre estrés psicológico y estrés físico.
B) alertar a las personas estresadas acerca de su grave situación.
C) demostrar fehacientemente que el estrés es una enfermedad.
D) describir las causas más frecuentes de estrés en la sociedad.
E) explicar que el estrés es inevitable en las sociedades modernas.

Solución:
En el último párrafo se establece con claridad la intención del autor: hacer un
llamado de alerta.
Clave: B
9. El autor combate la siguiente opinión:

Ciclo 2009-II

A) El estrés afecta a un 80% de la población mundial en la actualidad.
B) Se puede estar orgulloso del estrés porque es un sinónimo de éxito.
C) El estrés puede acarrear desastrosos efectos en el organismo humano.
D) En las personas, el estrés puede ocasionar desequilibrio y baja autoestima.
E) Los músculos de las sienes se ven afectados en una condición de estrés.

Solución:
El estrés es una anomalía, y, por lo tanto, no hay que estar orgulloso de padecerlo.
Clave: B

10. ¿Cuál es la mejor síntesis para el texto?

A) El estrés es un estado de desajuste con el entorno que se puede manifestar por
ciertas perturbaciones mentales, así como en una afección física a los músculos,
con efectos desastrosos en el organismo.
B) Las personas con un agudo cuadro de estrés manifiestan estados depresivos,
una gran sensibilidad frente a toda situación, exceso de ansiedad y miedo por
cualquier circunstancia considerada adversa.
C) Hay dos tipos de estrés; el primero es denominado psicológico y entraña una
tensión mental permanente con pensamientos perturbados; el segundo, llamado
físico, se manifiesta en la tensión muscular.
D) El estrés es considerado como una sobrecarga de trabajo y de problemas, y se
considera que, en las situaciones laborales de nuestra época, el estrés crea
inestabilidad, lo cual acarrea enfermedades.
E) Muchas personas consideran que el estrés es algo natural en un entorno social
competitivo y, en consecuencia, refutan que el estrés sea visto como una
enfermedad; es solamente un problema pasajero.

Solución:
En resumidas cuentas, el autor define el estrés, presenta sus dos tipos y alerta sobre
sus terribles consecuencias.
Clave: A

11. Si alguien sostuviera que el estrés es una enfermedad,

A) podría apoyarse en la actual definición de estrés.
B) expresaría una opinión científicamente rebatible.
C) aseveraría un hecho científicamente objetivo.
D) se trataría de una opinión altamente probable.
E) daría un paso enorme para salir de sus problemas.

Solución:
El estrés es una reacción del organismo ante un entorno amenazante, no es una
enfermedad.
Clave: B
12. En conclusión, el autor señala que el estrés es

A) la explicación más certera a los problemas de concentración.
B) un padecimiento que ataca a todas las personas exitosas.
C) una tensión cuyo origen radica en el músculo trapecio.

Ciclo 2009-II

D) un estado anómalo con desastrosas consecuencias.
E) la mejor respuesta del organismo frente a un problema.

Solución:
En última instancia, el autor sostiene que el estrés no debe ser considerado como
una situación normal.
Clave: D


Ciclo 2009-II

Universidad del Perú, DECANA DE AMERICA

Habilidad Lógico Matemática
EJERCICIOS DE CLASE Nº 1

1. Se tiene la siguiente información:
- Algunos profesores ganan S/. 5 000,
- algunos profesores son ingenieros, y
- todos los ingenieros ganan S/ 5 000.
¿Qué afirmación es correcta?
A) Ninguno que gana S/. 5 000 es ingeniero
B) Ningún profesor es ingeniero
C) Todos los que ganan S/. 5 000 son profesores.
D) Algunos profesores que no ganan S/. 5 000 no son ingenieros.
E) Todos los profesores son ingenieros.

Solución Ganan S/. 5000
Profesores
Ingenieros

Rpta: D

2. Nicolás en una tabla anota los goles a favor y en contra, de tres equipos que se en-
frentaron entre sí en tres partidos de fútbol; pero se olvidó de llenar una casilla.
¿Cuál fue el resultado del partido entre Alianza y Cristal, en ese orden?

A) 2−1 Equipo GF GC
B) 1−0 UNIVERSITARIO 5 0
C) 2−0 ALIANZA 4
D) 3−1 CRISTAL 1 4
E) 3−0

Solución
Como Goles a Favor = Goles en Contra
Entonces Alianza tiene 2 goles a favor y como Universitario no recibió ningún gol
Los partidos quedaron de la siguiente manera:
Universitario - Alianza: 3-0
Universitario – Cristal: 2-0
Alianza – Cristal: 2-1 Rpta: A


Ciclo 2009-II

3. Luchito, Betito, Julito y Carlitos tienen 14, 16, 17 y 19 monedas de S/. 5, aunque no
necesariamente en ese orden. Se sabe lo siguiente:
- La suma de las cantidades de monedas que tienen Luchito y Betito, resulta un
número primo;
- la suma de las cantidades de monedas que tienen Betito, Julito y Carlitos, resulta
un número par; y
- la suma de las cantidades de monedas que tienen Betito y Julito, resulta un núme-
ro impar.
¿Cuánto dinero tienen Carlitos y Luchito juntos?

A) S/. 175 B) S/. 150 C) S/. 165 D) S/. 180 E) S/. 155
Solución

L + B = Nro primo; B + J + C = Nro. par; B + J = Nro.impar

14 + 17 = 31; 17 + 16 + 19 = 52; 17 + 16 = 33
C + L = 19 +14 = 33 Rpta: C

4. Una hoja rectangular de papel milimetrado tiene 231 mm de ancho y 4 mm de altura.
Si trazamos una línea recta desde un vértice hasta el vértice opuesto, ¿cuántos cua-
draditos de 1 por 1mm son atravesados por la línea?

A) 231 B) 235 C) 233 D) 232 E) 234

Solución

1) Desde que MCD(231, 4) = 1, la diagonal no pasa por ningún nodo interior.
2) La diagonal interseca a las 3 rectas horizontales interiores.
3) Número de cuadraditos atravesados por la diagonal: 231 + 3 = 234.
Rpta: E

5. ¿Cuántos de los siguientes enunciados son falsos?
i. Exactamente uno de los enunciados de esta lista es falso.
ii. Exactamente dos de los enunciados de esta lista son falsos.
iii. Exactamente tres de los enunciados de esta lista son falsos.
iv. Exactamente cuatro de los enunciados de esta lista son falsos.
v. Exactamente cinco de los enunciados de esta lista son falsos.
vi. Exactamente seis de los enunciados de esta lista son falsos.
vii. Exactamente siete de los enunciados de esta lista son falsos.
viii. Exactamente ocho de los enunciados de esta lista son falsos.
ix. Exactamente nueve de los enunciados de esta lista son falsos.
x. Exactamente diez de los enunciados de esta lista son falsos.

A) 9 B) 7 C) 6 D) 8 E) 10


Ciclo 2009-II

Solución

1) El enunciado ix es verdadero y todos los demás son falsos.
2) Por tanto, 9 enunciados son falsos.
Rpta: A

6. Durante todos los días del mes de marzo, Óscar sale a pasear en compañía de
Ruth, Luisa o María. Con Ruth sale 20 días, 18 días con Luisa y el 24 de marzo sale
solo con María. ¿Cuántos días salió con Ruth y Luisa a la vez?

A) 7 B) 6 C) 10 D) 8 E) 9

Solución

Ruth Luisa 20 + (18 – x)+ 1 = 31
Maria
∴ x = 8 días

20 - x 18-x 1
x

Rpta.: D

7. A una reunión asistieron 109 personas. Se sabe que 16 mujeres tenían 17 años, 34
asistentes tenían 24 años, 23 mujeres no tenían ni 17 ni 24 años. Si hubo 51 hom-
bres, de los que 32 no tenían 17 años, ¿cuántos hombres no tenían 17 ni 24
años?

A) 15 B) 17 C) 19 D) 18 E) 14
H(51) M(58)
Solución
17 años

c 16
1. a + b = 34
d 23
2. d + a = 32
3. 16 + 23 + b = 58 → b = 19
a b
4. 3) en 1) y 2 : a = 15
d = 17


Ciclo 2009-II

8. En una fiesta de fin de semana asistieron un total de 96 personas. Se sabe que el
número total de hombres es igual al número de mujeres solteras. Si hay 18 hombres
casados y hay más de 29 mujeres casadas. ¿Cuántas personas son solteras si entre
ellos hay más de 14 hombres?

A) 28 B) 32 C) 36 D) 48 E) 56

Solución

Hombres Mujeres Total
De los datos Casados 18 96-2x 114-2x
i) 96 - 2x > 29 entonces 33.5 > x Solteros x-18 x 2x-18
ii) x – 18 > 14 entonces x > 32 Total x 96-x 96
iii) De i) y ii) x = 33
∴ Nro. personas solteras = 2x – 18 = 48
Rpta.: D

9. Diego dispone de cierta cantidad de dinero para ir al circo con sus sobrinos. Si
compra entradas de 30 soles le faltaría 12 soles, y si compra entradas de 20 soles le
sobraría 38 soles. ¿Cuantos sobrinos tiene Diego?

A) 8 B) 3 C) 5 D) 4 E) 6

Solución

Nº- de sobrinos : x
Dinero disponible: D de dato: 30 ( x + 1) − 12 = D y 20 ( x + 1) + 38 = D
Luego 30x + 30 − 12 = 20x + 20 + 38 luego x=4
Rpta.: D

10. Once amigos consumieron igual cantidad de dulces, por los que cada uno debe pa-
gar una misma cantidad de soles. Dos de ellos solo pueden pagar la mitad y otros
tres solo la tercera parte de lo que les corresponde, obligando de este modo a cada
uno de los restantes a pagar S/. 18 más de lo que le corresponde. ¿Cuántos soles
debería haber pagado cada uno inicialmente?

A) 36 B) 26 C) 24 D) 21 E) 19

Solución

Cada uno debe pagar: x
Total de la deuda : 11x
Dato:
⎛x⎞ ⎛x⎞
2 ⎜ ⎟ + 3 ⎜ ⎟ + 6 ( x + 18 ) = 11x
⎝2⎠ ⎝3⎠
∴ x = 36
Rpta.: A


Ciclo 2009-II

11. Si cada asistente a una reunión benéfica colabora con S/. 5, faltaría S/. 180 para
reunir el aporte requerido. Si cada asistente colabora con S/. 8, se reuniría
S/. 180 más de lo requerido. ¿Cuánto debe aportar cada asistente para que no fal-
te ni sobre?

A) S/. 5, 50 B) S/. 5, 60 C) S/. 6, 60 D) S/. 6, 50 E) S/. 7, 80

Solución

x = # de asistentes
Aporte : 5x + 180 = 8x – 180 ⇒ x = 120
Aporte = 780
780
cada uno debe aportar = = 6,5 soles. Rpta.: D
120

12. ¿Cuál es la menor longitud que debe recorrer la punta de un lápiz para realizar el
dibujo rectangular sin levantar el lápiz del papel?
B 3cm P 3cm C
A) 43cm

B) 44cm

C) 45cm 4cm 4cm

D) 40cm

E) 47cm
A 3cm Q 3cm D
Solución

#VImpares = 4
4−2
#TR = =1
2
L.min = 2(4) + 2(3 + 3) + 4(5) + 4 = 44 cm
{
144424443 Re pite
Total
Rpta.: B

13. En la figura MNPQ es un rectángulo y las circunferencias tienen un radio de 2 cm.
¿Cuál es la menor longitud que debe recorrer la punta de un lápiz para realizar el di-
bujo sin levantar el lápiz del papel?
N P
A) 8 ( 6 + π ) cm
B) ( 48 + 9π ) cm
C) ( 46 + 9π ) cm
D) 9 ( 6 + π ) cm
E) 10 ( 5 + π ) cm
M Q

Ciclo 2009-II

Solución
#VImpares = 8,
8−2
#TR = =3
2
⎛ ⎞ ⎛ ⎞
Lmin = ⎜ 3(8) + 5(4) + 2(2π(2)) ⎟ + ⎜ 242 + π ⎟ = ( 48 + 9π ) cm
{ 1 24 ⎟ ⎜ 1 3 ⎟ +24
⎜ { 4 3
⎝ horizontales verticales Lc ⎠ ⎝ Repite ⎠
Rpta.: B

14. Se tiene un alambrado formado por un cubo y una pirámide regular cuyas caras la-
terales son triángulos equiláteros en donde la arista mide 40 cm. Hallar la distancia mí-
nima que recorrerá una hormiga situada en el punto V, al desplazarse por todo el alam-
brado.

V
A) 6,8 m

B) 8 m

C) 7,2 m

D) 7,6 m

E) 6,4 m

Solución

#VImpares = 4,
4−2
#TR = =1
2
Caso I
⎛ ⎞
Lmin = ⎜ 40 + 40 + 16(40) ⎟ + 1(40) = 7,6 m
⎜ 1 244 3 123 ⎟ {
Llevar a Vimpar
⎝ aristas ⎠ Repite

Caso II
Lmin = 16(40) + 2(40) = 7,2 m
123 {
aristas Repite

Rpta.: C


Ciclo 2009-II


Habilidad Lógico Matemática
EVALUACIÓN DE CLASE Nº 1

1. Solamente dispones de dos relojes de arena, cuyas capacidades son de 8 minutos y
de 5 minutos. ¿Cuántas vueltas como mínimo debemos realizar a estos relojes para
medir solo con ellos un intervalo de 11 minutos?

A) 2 B) 3 C) 5 D) 4 E) 1

Solución
1) Ponemos a vaciar simultáneamente los dos relojes de arena.
2) Cuando se termine de vaciar el de 5, quedará tres minutos todavía al de 8.
3) Le damos la vuelta al de 5 inmediatamente, con lo que cuando termine el de 8, es
decir, cuando hayan pasado 8 minutos, habrán transcurrido tres en el de 5.
4) Por lo que, inmediatamente le damos la vuelta al de 5 para que termine dentro de
tres minutos, que sumados a los 8 minutos medidos en el reloj de 8, son los 11
minutos que se pretendían medir.
5) Por tanto solo dos vueltas, para medir 11 minutos.
Rpta.: A

2. Betsy, Gladys y Mary son amigas. Una es soltera, otra es casada y otra es viuda
aunque no necesariamente en ese orden. Se sabe que:
- Mary no es casada y debe S/.7 a la verdulera.
- La viuda y Betsy sólo deben a la carnicera.
¿Qué afirmación es correcta?

A) Gladys es viuda B) Betsy es viuda C) Betsy es soltera
D) Mary es casada E) Mary es viuda
Solución:
Mary debe a la verdulera
La viudad sólo debe a la carnicera
Mary no es viuda y Gladys es viuda
Rpta.: A


Ciclo 2009-II

3. Cuatro amigos tienen la siguiente cantidad de panes y soles:

Amigos Panes Dinero (s/.)
M 0 10
N 2 2
P 3 0
Q 5 0

Si todos consumen igual cantidad de pan y al final se reparten el dinero entre los
que aportaron para los otros, ¿cuánto dinero le corresponde a Q?

A) S/. 5 B) S/. 8 C) S/. 10 D) S/. 6,5 E) S/. 7

Solución

- Se divide cada pan en 4 trozos: se tiene 10x4 = 40 trozos
- Todos comen igual : 10 trozos cada uno
- M come 10 trozos de otros
- N come 2 trozos de otros
- P dona 12-10: 2 trozos
- Q dona 20-10: 10 trozos
- Las donaciones son 12 trozos y corresponde darles 12 soles
- Por lo tanto a Q le corresponde: S/.1x10 = 10 soles
Rpta.: C

4. De 100 deportistas, se tiene que 60 practican básquet, 35 practican futbol y 25
practican vóley. Si solo 10 practican los 3 deportes, ¿cuántos practican solo un depor-
te?

A) 55 B) 80 C) 90 D) 65 E) 70

Solución
U(100)

B(60) F(35)
De los que juegan básquet: 75-(a+b) b
a
60 = a + 10 + 75 – (a + b) + 65 – (a + c)
∴ a + b + c = 90 10
65-(a+c) 40-(b+c)

c

V(25)

Rpta.: C


Ciclo 2009-II

5. En un campeonato de fútbol participan 84 jugadores de 35 a 3 8 años, de los
cuales se sabe lo siguiente:
• Hay 21 que tienen ojos negros, pero no tienen 35 años.
• Hay 6 que no tienen ojos negros ni marrones y no son menores de 37 años.
• De los que no son mayores de 36 años, 32 no tienen ojos negros ni marrones.
¿Cuántos jugadores de 35 años tienen ojos negros, si ellos son
la cuarta parte del total de jugadores que tienen ojos marrones?.

A) 5 B) 6 C) 7 D) 8 E) 4

Solución 35 años 36 años 37 años 38 años Total

Ojos Negros x 21 x + 21

Ojos Marrones 4x 5x + 59 = 84
Ojos ni negros ∴x = 5
32 6 38
ni marrones Rpta.:A
84
Total

6. Ocho niños compraron igual cantidad de dulces, por los que cada uno debe pagar
una misma cantidad de soles. Dos de ellos sólo pueden pagar la mitad y otros dos sólo
la cuarta parte de lo que les corresponde, obligando de este modo a cada uno de los
restantes a pagar S/.10 más de lo que le corresponde. ¿Cuánto debía pagar cada uno?

A) S/.28 B) S/.25 C) S/.18 D) S/ 16 E) S/.21

Solución

Cada uno debe pagar: x
Total de la deuda: 8x
Dato:
⎛x⎞ ⎛x⎞
2 ⎜ ⎟ + 2 ⎜ ⎟ + 4 ( x + 10 ) = 8x
⎝2⎠ ⎝4⎠
∴ x = 16
Rpta.: D

7. Los ahorros de un jubilado constan de (x + 1), (2x + 12) y (x – 2) billetes de 20,
50 y 100 soles respectivamente. Si al cambiarlos en billetes de 10 soles el número de
billetes obtenidos es 130, ¿cuántos billetes tenía al inicio?

A) 31 B) 23 C) 27 D) 35 E) 21

Solución


Ciclo 2009-II

20(x + 1) + 50(2x + 12) + 100(x – 2) = 130 (10)
22x = 88 ⇒ x = 4
Nro. De billetes que tenía al inicio = 4x + 11 = 4(4) + 11 = 27
Rpta.: C

8. En la figura, ABCD, DCEF y FEGH son rectángulos congruentes. Calcular la me-
nor longitud que debe recorrer la punta de un lápiz sin levantarla, para realizar la figu-
ra.

A) 83 cm B 4 cm C E G

B) 93 cm
3 cm 3cm
C) 73 cm
A
D F 4 cm H 4cm D
D) 63 cm 2 cm
R
E) 80 cm

Solución
#Vi = 8
8-2
#T.R.= =3
2
Lmin = 7(4) + 4(3) + 6(5)+ 2 + 343 + 5 = 83 cm
+ 3
1 24
EF+CD+RB
Rpta.: A

9. La longitud mínima que recorrió la punta del lápiz para realizar la siguiente figura

sin levantar el lápiz del papel es 205 cm. Hallar n, si ABCD es un rectángulo y las

longitudes son dadas en centímetros.

B 1 2 3 ... n C
1 1
1 1
A 1 2 3 ... n D

A) 7 B) 8 C) 9 D) 10 E) 11

Solución


Ciclo 2009-II

#Vi = 2n
2n − 2
#T.R.= = n −1
2
3n(n + 1)
205 = + 2(n + 1) + 2(n − 1)
2
∴ n = 10 Rpta.: D


Ciclo 2009-II


Aritmética
SEMANA Nº 01

TEORÍA

TABLAS DE VERDAD

1) Negación. Se denota mediante el 4) Disyunción fuerte
símbolo “~” y se lee “no es cier-
to que …” o “es falso que … p q pΔq
”.
V V F
p ~p V F V
F V V
V F F F F
F V

2) Conjunción 5) Condicional

p q p∧q p q p →q

V V V V V V
V F F V F F
F V F F V V
F F F F F V

3) Disyunción débil 6) Bicondicional

p q pvq p q p↔q

V V V V V V
V F V V F F
F V V F V F
F F F F F V


Ciclo 2009-II

PRINCIPALES EQUIVALENCIAS E IMPLICACIONES LÓGICAS
(LEYES DEL ALGEBRA PROPOSICIONAL)

1) Involución o doble negación 9) Leyes de absorción
~ (~ p) ≡ p a) [p v (p ∧ q)] ≡ p

2) Idempotencia b) [p ∧ (p v q)] ≡ p
c) [p v (~ p ∧ q)] ≡ (p v q)
a) Con respecto a la disyunción
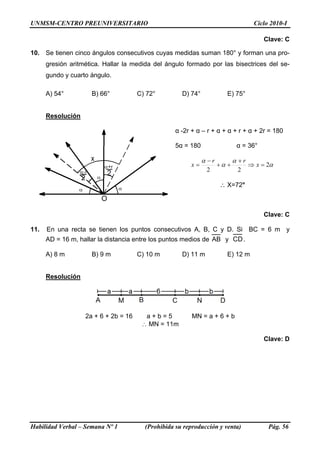
(p v p) ≡ p d) [p ∧ (~ p v q)] ≡ (p ∧ q)
b) Con respecto a la conjunción 10) Ley de la Negación de la Condicional
(p ∧ p) ≡ p
~ (p → q) ≡ p ∧ ~ q
3) Conmutatividad
11) Ley de la Condicional
a) Con respecto a la disyunción
(p v q) ≡ (q v p) p→q≡~pvq

b) Con respecto a la conjunción 12) Ley de la condicional contrarrecí-
(p ∧ q) ≡ (q ∧ p) proca
p→q≡~q→~p
4) Asociatividad
a) Con respecto a la disyunción 13) Ley de la Bicondicional
[(p v q) v r] ≡ [p v (q v r)]
a) (p ↔ q) ≡ [(p → q) ∧ (q → p)]
b) Con respecto a la conjunción
b) (p ↔ q) ≡ [(~ p v q) ∧ (~ q v p)]
[(p ∧ q) ∧ r] ≡ [p ∧ (q ∧ r)]
c) (p ↔ q) ≡ [(~ p ∧ ~ q) v (p ∧ q)]
5) Distributividad d) (p ↔ q) ≡ [~ (p v q) v (p ∧ q)]
a) De la conjunción respecto a la
disyunción 14) Ley de la diferencia simétrica
[(p v q) ∧ r] ≡ [(p ∧ r) v (q ∧ r)] a) p Δ q ≡ ~ (p ↔ q)
b) De la disyunción respecto a la b) p Δ q ≡ (p v q) ∧ ~ (p ∧ q)
conjunción
[(p ∧ q) v r] ≡ [(p v r) ∧ (q v r)] 15) Ley de Transportación
(p → q) ∧ (q → r) ⇒ (p → r)
6) Leyes de Morgan
a) ~ (p v q) ≡ (~ p ∧ ~ q) 16) Ley de Adición

b) ~ (p ∧ q) ≡ (~ p v ~ q) p⇒pvq

17) Ley de simplificación
7) Ley de la identidad
p∧q⇒p
Se denota T = Tautología F
= Contradicción, se tiene:

a) (p ∧ T) ≡ p b) (p ∧ F) ≡ F
c) (p v T) ≡ T d) (p v F) ≡ p

8) Ley del complemento
a) (p ∧ ~ p) ≡ F b) (p v ~ p) ≡ V


UNMSM-CENTRO PREUNIVERSITARIO Ciclo 2010-I

SOLUCIONARIO DE LOS EJERCICIOS DE CLASE N° 1

1. Si la proposición ∼[ ( q → s ) → ( p → r ) ] es verdadera, halle el valor de verdad
de cada una de las siguientes proposiciones, en el orden indicado.

I) ( ∼ s → ∼ q ) Δ ( r → p )
II) ∼ ( q ∧ ∼ s ) ∧ ( p ∧ ∼ r )
III) ( p ∧ q ∧ r ∧ s ) ∨ ( p ↔ r )

A) FVF B) VFV C) VVV D) FVV E) FFF

Solución:

q→s≡∼q∨s≡V i) V Δ V ≡ F
p→r≡F ∴ p ≡V ii) V ∧ V ≡ V
q = F iii) F ∧ F ≡ F
Rpta.: A

2. Si pθq ≡( p∧q )∨ ∼( ∼ p ∧ q ) , halle una proposición equivalente a la proposición
compuesta [ ( p θ ∼ q ) θ ∼ p ] ∧ ∼ [ ( p θ r ) ∨ ( q θ r ) ]

A) p ∨ ∼ p B) q ∧ ∼ q C) p D) p ∧ q E) p ∧ q

Solución:

pθq≡p∨∼q
*[ ( p ∨ q ) ∨ p ] ∧ ∼ [ p ∨ q ∨ ∼ r ]
p∨q∧∼(p∨q)∧r

F∧r≡F
Rpta.: B

3. Si la proposición ( p → ∼ q ) ∨ ( ∼ r → s ) es falsa, halle el valor de verdad de
cada una de las siguientes proposiciones, en el orden indicado

I) ( ∼ p ∧ ∼ q ) ∨ ∼ q
II) [ ( ∼ r ∨ q ) ∧ q ] ↔ [ ( ∼ q ∨ r ) ∧ s ]
III) [ p → r ] → [ ( p ∨ q ) ∧ ∼ q ]

A) VVV B) FFF C) FFV D) FVF E) VVF

Solución:

p→∼q≡F Reemplazando:
p=V ; q≡V I) F II) F III) V

∼r→s≡F
r=F ; S=F
Rpta.: C

Habilidad Verbal – Semana Nº 1 (Prohibida su reproducción y venta) Pág. 36


4. Si la proposición es falsa y VV(t)=V, halle los
valores de p , q y r , en el orden indicado.

A) VVF B) FVF C) VVV D) FFV E) FFF

Solución:

(∼ p → q ) ∨ ∼ ( r Δ q) ≡ F
p=F FFV
d=F
r=V
Rpta.: D

5. Se define el operador lógico mediante la siguiente tabla

p q p@q
V V F
V F F
F V F
F F V

Simplifique (p@q)@ (q@p)

A) ~p ∧ ~q B) p ∧ ~q C) ~p ∧ q D) p ∧ q E) p ∨ q

Solución:

p q (p@q) @ (q@p)
V V F V F
V F F V F
F V F V F
F F V F V

∴p∨q
Rpta.: E

6. Simplifique la siguiente proposición compuesta

[ ( p ∧ q ) ∨ ( p ∧ ∼ q ) ] ∨ [∼ p ∧ ∼ q ]

A) q → p B) p → q C) p D) q E) p ~p

Solución:

p∨(∼p∧∼q)
p∨∼q≡q→p
Rpta.: A



7. Dada la proposición “Hoy no veo televisión ni estudio porque no hay luz”
¿Cuáles de las siguientes proposiciones son verdaderas?

I. Hay luz dado que hoy veo televisión o estudio
II. Hay luz y no es cierto que hoy vea televisión o estudie
III. Hay luz o no es cierto que hoy vea televisión o estudie

A) I y II B) sólo II C) sólo I D) I y III E) Todas

Solución:

p : veo televisión I)r∨∼(p∨q)
q : estudio (p∨q)→r
r : hay luz III) r ∨ ∼ ( p ∨ q )
“ ∼ r → ( ∼ p ∧ ∼ q )”
Rpta.: D

8. Simplificar la proposición:

“No es cierto que José sea una persona tranquila y contador, entonces José es
profesor o no es una persona tranquila; además José es profesor”

A) José es tranquilo B) José es contador
C) José es tranquilo y contador D) José es contador y profesor
E) José es profesor

Solución:

p : José es tranquilo [ ∼ ( p ∧ q) → ( r ∨ ∼ p ) ] ∧ r
q : José es contador [(p∧q)∨ r∨∼p ]∧r
r : José es profesor r
Rpta.: E

9. Simplifique la proposición compuesta

t→{[(p→q)→q]∧[∼p∧(q→p]}

A) ~q B) ~p C) ~t D) p q E) q t

Solución:

t→{[( p∧∼q)∨q]∧ [∼p∧(∼q∨p)]}
t→{ ( p∧ q)∧ [∼p∧ ∼q) }
t→{[( p∨q)∧ ∼(p∨q)}
t→F≡∼t
Rpta.: C



10. Se define el operador * tal que

p ∗ q ≡ (∼p∨∼q)↔(p∧q)

Determinar el valor de verdad de las siguientes proposiciones

I) (p ∗ q)∨(p∨∼p)
II) (p ∗ q)∧(p∧∼p)
III) (p ∗ q)→r
IV) (p∨∼p)→(p ∗ p)

A) VVVF B) VFFV C) FVFV D) FFFV E) VFVF

Solución:

p ∗ q≡∼(p∧q)↔p∧q≡F

I) V II) F III) V IV) F
Rpta.: E

11. Se define:

I) p q≡∼p→q II) p Δ q ≡ ∼ q

Simplificar: {(p q)→(qΔp)}∧{pΔ(q q)}

A) ∼ q B) p ∧ q C) ∼ p ∨ q D) ∼ ( p ∨ q ) E) ∼ p

Solución:

p q≡p∨q {∼(p q)∨∼p }∧{∼(q q)}
pΔq≡∼q {(∼(p∧∼q)∨∼p }∧∼q
∼p∧∼q≡∼(p∨q)
Rpta.: D
12. Si se cumple:
(∼p∧q)→(p∨r)≡(s∨t)↔(∼s∧∼t)

Simplificar: [ ( p ∧ r ) → ( s ∨ t ) ∧ ( q ∧ t )

A) s ∨ t B) ∼ t C) ∼ s D) t E) s

Solución:

(∼p∧q)→(p∨r)≡(s∨t)↔∼(s∨t)
p∨∼q∨r≡F V∧t≡t
p≡F ; q ≡V ; r≡F
Rpta.: D




Aritmética
EVALUACIÓN DE CLASE N° 1

1. Si la proposición ( r Δ s ) ∨ ∼ ( p → q ) falsa, simplifique la proposición com-
puesta [ ( p ∧ ∼ q ) → r ] ∧ { [ ( ∼ r ∧ s ) ↔ q ] → p }

A) p ∨ q B) p ∨ q C) ~p D) ~ r E) r ~ p

Solución:

V∧{ [F↔q]→p}
∼q→p
q∨p
Rpta.: A

2. Simplificar la proposición compuesta

∼{[(∼p∧∼q)∨(p∧(∼p∨q))]→∼(p∨q)}

A) p ∨ q B) p ∧ q C) p q D) p q E) p ∨ ~q

Solución:

∼{[(∼p∧∼q)∨(p∧q)}→∼(p∨q)} ; ∼{∼(p∨q)∨∼(p∧q)}
p∨q∧(p∧q)
∼{[(p∨q)∧∼(p∧q)]∨∼(p∨q)} ; p∨q
Rpta.: A

3. Si las proposiciones ( p ∧ q ) y ( q → t ) son falsas, halle el valor de verdad
de las siguientes proposiciones, en el orden que se indica
I) (~p ∨ t ) ∨ s
II) ~ [ p ∧ ( ∼ q ∨ ∼ p ) ]
III) [ ∼ p ∨ ( q ∧ ∼ t ) ] ↔ [ ( p → q ) ∧ ∼ ( q ∧ t ) ]

A) FVF B) VVF C) VVV D) VFV E) FVV

Solución:

q≡V ; t=F ∴ p≡F
I) V II) V III) V
Rpta.: C



4. Si la proposición [ ∼ ( p ∼ →

, es falsa, halle el valor de p, q, r y s en el orden indicado.

A) VFFF B) VVVF C) FVFV D) VFVF E) VFFV

Solución:

p≡V r≡V V F V F
q≡F s≡S
Rpta.: D

5. Se define el operador lógico mediante la siguiente tabla

p q P@q
V V F
V F F
F V V
F F F
Simplifique la proposición compuesta [ p @ ( ∼ p @ q ) ] @ q

A) ~q B) ~p C) p ∧ q D) p E) q

Solución:

p@q≡∼p∧q
[∼p∧(p∧q)]@q
F@q≡V∨q ≡q
Rpta.: E

6. Simplifique la proposición compuesta

(p∧q)∨∼[(p∨q)→(p∧q)]∨(p∨q)

A) p q B) p q C) ~p D) ~q E) ~p q

Solución:

(p∧q)∨(p∨q)∨∼[∼(p∨q)∨(p∧q)]
(p∨q)∨[(p∨q)∧∼(p∧q)]
p∨q

Rpta.: A



7. Halle el valor de verdad de cada una de las siguientes proposiciones, en el or-
den que se indica

p: 5 < 8 ↔ [ 6 < 1 ↔ 1 ≤ 2 ]
p: 2 < 3 ↔ { [ 4 > 5 ↔ 2 ≤ 3 ] Δ 2 < 3 }
r:(p,q)∨(∼p , q)

A) VVV B) FVV C) FFV D) FVF E) FFF

Solución:

p:V↔F≡F
q:V→V=V
r:∼p∨q∨p∨q≡V
Rpta.: B

8. “Si Adán comió la manzana entonces Eva lo tentó”, equivale a

A) Si Adán no comió la manzana, entonces Eva lo tentó
B) Adán no comió la manzana pero Eva lo tentó
C) o Eva lo tentó o Adán comió la manzana
D) Si Eva no lo tentó, Adán no comió la manzana
E) Ya que Eva lo tentó, Adán no comió la manzana

Solución:

p : Adam comió la manzana ∼q→∼p
q : Eva lo tentó q∨∼p
p→q
Rpta.: D

9. Si la proposición [ ( p ∧ ∼ q ) ∧ ( r → q ) ] ∧ [ ( ∼ p ∨ q ) → ( p ∧ q ) ] es verdadera,
halle el valor de p, q y r , en el orden que se indica.

A) VFF B) FVV C) VVV D) FFV E) VFV

Solución:
p∧∼q∧∼r ∧[p∧∼q∨(p∧q)]
p∧∼q∧∼r∧p∧∼q
p∧∼q∧∼r≡V

p≡V q≡F r≡F

Rpta.: A



10. De las siguientes proposiciones:

I) Es necesario que Juan no vaya al cine para que termine su tarea.
II) No es cierto que Juan termine su tarea y vaya al cine.
III) Juan no termina su tarea y no va al cine.

¿Cuáles son equivalentes?

A) I y II B) II y III C) I y III D) I, II y III E) Ninguna

Solución:

p: Juan va al cine I) q → ∼ p
q : Juan hace tarea II) ∼ q ∧ p
III) ∼ q ∧ ∼ p
Rpta.: E



Álgebra
EJERCICIOS DE CLASE N° 1

x+3 x+2 2
1. Resolver la ecuación + = 2 , y dar como respuesta x − .
x−2 x−3 5

5 2 21 11
A) B) C) D) E) 0
2 5 10 10

Solución:

2 2
x −9+x −4
= 2 → 2x2 – 13 = 2(x2 -5x+6)
( x − 2)( x − 3)
5 2 5 2 21
10x = 25 → x = entonces x − = − =
2 5 2 5 10

Clave: C

2 4 6 +
2. Resolver la ecuación en x : − = , m ∈ Z y m ≠ 6.
mx − 3 3x 3 − mx

m−3 m−6 3 m−6 2
A) B) C) D) E)
2 m +1 m−6 2 m−6

Solución:

2 6 4 8 4
− = → = → 6x = mx – 3
mx − 3 3 − mx 3x mx − 3 3 x
3
x(m – 6) = 3 → x =
m−6
Clave: C



3. Resolver

x −1 x −1 3 1 1
+ = − +
x2 + 1 2x 2 − x x2 + 1 2x − 1 x

A) 1 B) 2 C) 3 D) 4 E) 5

Solución:

x −1 x −1 3 1 1 x −1 3 1 x −1 1
+ = − + → − =− − +
2
x +1 x(2x − 1) x + 1 2x − 1 x
2
x +1
2 2
x +1 2x − 1 x(2x − 1) x
x−4
=0 → x=4
x2 + 1

Clave: D

b +1 2 c +1 a +1
4. Si la ecuación en x , a bcx + b cax + c ab = 0 , (a, b, c > 0) tiene soluciones
iguales, calcular

c
b
M = 1+
b a
a c

A) 5 B) 2 C) 3 D) 3 E) 2

Solución:

Como sus soluciones son iguales Δ = 0
c +1
Δ = (b ca)2 − 4(ab +1bc )(c a +1ab) = 0
c +1
Entonces (b ca)2 = 4(ab + 2b 2c a + 2 ) → b2c + 2c 2a 2 = 4(ab + 2b 2c a + 2 )

b
2c b a
= 4a c →
(b ) c 2
=4 →
b
c
=2
ab c a a c
b a

c
b
M = 1+ = 3
b a
a c
Clave: D



5. Si la diagonal de un terreno rectangular mide 130 m y su área es 6 000 m². ¿Cuántos metros
mide su perímetro?

A) 360 m B) 350 m C) 340 m D) 400 m E) 380 m

Solución:

Sean los lados x e y se tiene x 2 + y 2 = 130 , x y = 6 000
2 2
x + y + 2xy = 16900 + 12000
2 2
(x + y) = 28900 = 170
Perímetro = 2(170) = 340m

Clave: C

6. Sonia y Martín encuentran una bolsa de caramelos. Sonia toma 2 caramelos y la sexta parte
del resto; luego Martín toma 3 caramelos y la sexta parte del resto y de esta manera los dos
han tomado el mismo número de caramelos. ¿Cuántos caramelos había en la bolsa?

A) 20 B) 22 C) 24 D) 26 E) 28

Solución:

Sea x el número de caramelos
x−2 5
Sonia : 2 + , queda ( x − 2) = y
6 6
y−3 1⎛5 ⎞
Martín : 3 + es decir 3 + ⎜ ( x − 2) − 3 ⎟
6 6⎝6 ⎠
x−2 1⎛5 ⎞
Luego 2 + = 3 + ⎜ ( x − 2) − 3 ⎟
6 6⎝6 ⎠
5
x – 2 = 6 + ( x − 2) − 3
6
6x – 12 = 18 + 5x – 10.
x = 20
Clave: A

7. Dos obreros realizan una obra en 10 días, uno de ellos es dos veces más rápido que su
compañero. ¿Cuántos días demorará el obrero más lento en realizar él sólo la obra?

1 1
A) 40 días B) 30 días C) 10 días D) días E) días
30 10

Solución:

1 1 1
Los dos juntos avanzan en un día : + =
x 3 x 10
4 1
luego = , 3x = 40.
3 x 10
El más lento demora 3x para completar la obra, es decir 40 días.

Clave: A



8. Hallar la suma de las soluciones enteras de la ecuación

2 2
x − x +1 x −x+4
− =1
2 2
x − x −1 x − x +1

A) – 2 B) – 1 C) 0 D) 1 E) 2

Solución:
2
Consideremos a = x – x
a +1 a + 4
Entonces − = 1 → (a + 1)2 – (a – 1)(a + 4) = (a – 1) (a + 1)
a −1 a +1
2
a +a–6=0
a=2óa=–3
2 2
Como a = x – x, si x – x = 2 entonces x = 2 ó x = – 1
2
si x – x = – 3 entonces no hay soluciones enteras.
Luego la suma de soluciones es : 2 – 1 = 1.

Clave: D

9. Junior gasta todos los días la mitad de lo que tiene, más 40 nuevos soles; al cabo de 5 días
ha gastado todo. ¿Cuántos nuevos soles tenía al principio?

A) 1 240 B) 2 480 C) 1 200 D) 2 440 E) 2 240

Solución:

Tenía x
x x
1) + 40 queda – 40 = A → x = 2 480
2 2
A A
2) + 40 queda – 40 = B → A = 1 200
2 2
B B
3) + 40 queda – 40 = C → B = 560
2 2
C C
4) + 40 queda – 40 = D → C = 240
2 2
D D
5) + 40 queda – 40 = 0 → D = 80
2 2
Clave: B



10. Dada la inecuación

2
x a+x a
+ ≥ , a > 0 ; x > 0, hallar una solución.
x + a a − x a2 − x 2

a 3a
A) B) C) 2a D) 3a E) 4a
2 2

Solución:

2 2 2 2
x − ax − ( x + 2ax + a ) a − 3ax
+ ≥0 → ≥0
2 2 2 2
x −a x −a x 2 − a2
3x
≤ 0 → ( x − a)( x + a) < 0
( x − a)( x + a)

– a < x < a luego como x > 0, 0 < x < a
Clave: A

EVALUACIÓN DE CLASE N° 1

2x − 1 x − 2
1. Si x0 es solución de la ecuación + = 3 , calcular 4x0 + 1.
x x +1

A) 0 B) 1 C) 2 D) 3 E) 4

Solución:

2 2
2x + x − 1 + x − 2x
= 3 → 3 x 2 − x − 1 = 3( x 2 + x ) → 4x = – 1
2
x +x
Luego 4x0 + 1 = –1 + 1 = 0

Clave: A

2. Hallar x de la ecuación

x−a x−2
+ = 2 , si se sabe que a ≠ ± 2, a ≠ 0.
x+a x+2

2a 4a −4+a a −a
A) − B) − C) D) E)
a+2 a+2 a−2 a +1 4a + 1



Solución:

x 2 + (2 − a)x − 2a + x 2 + (a − 2)x − 2a
= 2; x ≠ −a x = −2
x 2 + (a + 2)x + 2a
2x 2 − 4a = 2( x 2 + (a + 2)x + 2a) → − 4a = (a + 2)x
− 4a
Luego x =
a+2

Clave: B

x 1
3. Resolver la ecuación en x, − = 1 , a ≠ ±1.
x−a x −b

ab + a ab − a ab − a
A) B) C)
a −1 a −1 b −1
ab + a ab − a
D) E)
b −1 a +1

Solución:

x 2 − bx − x + a 2 2
=1 → x − bx − x + a = x − ax − bx + ab
( x − a)( x − b)

ab − a
(a − 1)x = ab − a → x =
a −1

Clave: B

4. Si el área de un triángulo rectángulo es 600 m² y la diferencia de la medida de los catetos es
10 m, calcular la medida de su hipotenusa.

A) 60m B) 40m C) 50m D) 70m E) 20m

Solución:

Catetos x, y

xy = 600(2) = 1200
y > x, y – x = 10 → (y – x)2 = 100
y2 – 2xy + x2 = 100 → x2 + y2 = 100 + 2(1200)

x2 + y2 = 2500 luego x 2 + y 2 = 50m
Clave: C



5. Un boticario tiene cierta cantidad de kilogramos de una sustancia química. Vende la cuarta
parte y compra 12 kilogramos, con lo cual tiene los 3/2 de la cantidad inicial. ¿Qué cantidad
de dicha sustancia química tenía el boticario?

A) 8 kg B) 16 kg C) 24 kg D) 32 kg E) 48 kg

Solución:

1 3
Vende x → Queda x
4 4

3 3
Por dato x + 12 = x luego 3x + 48 = 6x → x = 16
4 2

Clave: B

6. José y Edwin tienen depositado en el Banco la cantidad de $38 000. Si los 3/5 de lo que
tiene José equivalen a los 2/3 de lo que tiene Edwin. ¿Cuánto tiene Edwin?

A) $ 20 000 B) $ 18 000 C) $ 12 000 D) $16 000 E) $24 000

Solución:

José : x Edwin: 38 000 – x
3 2
Por dato x = (38000 − x )
5 3
9x = 10(38 000 – x)
9x = 10×19×2 000 – 10x
19x = 10×19×2 000
x = 20 000
Edwin tiene $ 18 000

Clave: B

7. De un depósito lleno de agua se extrae la octava parte, ¿qué fracción del resto se debe
sacar para que quede solo los 5/7 de su capacidad inicial?

3 2 2 8 9
A) B) C) D) E)
29 9 49 49 49

Solución:



Sea “x” la capacidad del propósito de agua
x
: La octava parte extraída
8
x 7
x− = x Agua que queda
8 8
⎛7 ⎞ 7
f ⎜ x ⎟ : Se saca “ f ” de los x de agua
⎝8 ⎠ 8

7 ⎛7 ⎞ 5
Del dato x − f⎜ x ⎟ = x
8 ⎝8 ⎠ 7
9
Luego f =
49

Clave: E

8. La edad actual de Javier es 3 veces más que la de Roxana. Si Javier hubiera nacido 7 años
después y Roxana 5 años antes, ambos tendrían la misma edad; ¿cuál es la diferencia de
sus edades?

A) 10 años B) 2 años C) 12 años D) 11 años E) 9 años

Solución:

Edad de Roxana: x años
Edad de Javier: 4x años
Si Javier hubiera nacido 7 años después, tendría 7 años menos: 4x – 7
Si Roxana hubiera nacido 5 años antes, tendría 5 años más: x + 5
Del dato 4x – 7 = x + 5
x=4
Luego Roxana: 4 años
Javier 16 años
Diferencia de edades = 12años

Clave: C




Geometría

1. En una recta se ubican los puntos consecutivos A, M, B, C, N y D, siendo M y N pun-
tos medios de AB y CD respectivamente. Si BC = 3m y MN = 9m, hallar AD.

A) 12m B) 15m C) 16m D) 20m E) 18m

Resolución

MN = a + b + 3 = 9 a+b=6
AD = a + 9 + b ∴ AD = 15m

Clave: B

2. En una recta se ubican los puntos consecutivos A, B, C, D y E. Si AB=CD,
BC + DE = 14m y numéricamente AB.DE = CD.AD, hallar BD.

A) 5m B) 6m C) 7m D) 8m E) 9m

Resolución

BC + DE = 14 x – a + x + a = 14 ∴ x = 7m

Clave: C

3. En una recta se tienen los puntos consecutivos A, B, C, D, E y F. Si
CD BE AF
= = y AD + BE + CF = 36m, hallar AB + EF.
3 4 5

A) 3m B) 5m C) 4m D) 2m E) 6m



Resolución

AD + BE + CD + DF = 36 AF + BE + CD = 36
5a + 4a + 3a = 36 12a = 36 a=3
∴AB + EF = 3

Clave: A

4. En una recta se tienen los puntos consecutivos A, B, C y D, luego se ubican los pun-
tos medios M y N de AB y CD respectivamente. Si AC = 8m y BD = 16m,
hallar MN.

A) 8 m B) 9 m C) 11 m D) 12 m E) 13 m

Resolución

2a + m = 8 ……..I I + II : 2(a + b + m) = 24
2b + m = 16 …….II a + b + m = 12
∴ MN = 12

Clave: D

5. En una recta se tienen los puntos consecutivos A, B, C y D. Si numéricamente
1 n 6
AB.CD = nBC.AD y + = , hallar n.
AD AB AC

A) 2 B) 7 C) 3 D) 4 E) 5

Resolución

CD nBC AD − AC n( AC − AB ) AC nAC
= ⇒ = ⇒ 1− = −n
AD AB AD AB AD AB

1 n n +1 6
+ = = ⇒∴ n = 5
AD AB AC AC



Clave: E
6. La suma de las medidas de dos ángulos es 120º y el complemento del primero es
igual a 11 veces el complemento del segundo. Hallar la razón de las medidas de los
ángulos.

6 5 9 7 8
A) B) C) D) E)
17 17 17 17 17

Resolución

α + β = 120° …I Cα = 11 Cβ 90° - α = 11(90° - β)
11β - α = 900° …II De I y II: β = 85° ⇒ α = 35°
α 7
∴ =
β 17

Clave: D

7. Se tienen los ángulos consecutivos AOB, BOC y COD, OX es bisectriz del ángulo
AOC y OY bisectriz de BOD. Si mAOB – mCOD = 18º y mXOY = 12º,
hallar mAOB.

A) 22º B) 21º C) 18º D) 20º E) 23º

Resolución

2α + β + 6 = 12 + β

α=3

∴ m AOB = 21°

Clave: B



8. En la figura, mAOC = mBOD y mAOD – 2mAOB = 30º. Hallar mBOC.

A) 48º
A
B) 28º B

C) 20º
C
D) 40º
O
D
E) 30º

Resolución

A
B x + 2θ - 2θ = 30°

C ∴ x = 30°

O
D

Clave: E

9. Se tienen los ángulos consecutivos AOB, BOC y COD. Si mAOB=70° y mCOD=20°,
hallar la medida del ángulo que determinan las bisectrices de los ángulos BOC y
AOD.

A) 20º B) 30º C) 25º D) 35º E) 38º

Resolución

2x + α + 20° = α + 70°

∴ x = 25°



Clave: C

10. Se tienen cinco ángulos consecutivos cuyas medidas suman 180° y forman una pro-
gresión aritmética. Hallar la medida del ángulo formado por las bisectrices del se-
gundo y cuarto ángulo.

A) 54° B) 66° C) 72° D) 74° E) 75°

Resolución

α -2r + α – r + α + α + r + α + 2r = 180

5α = 180 α = 36°

α −r α +r
x= +α + ⇒ x = 2α
2 2

∴ X=72°

Clave: C

11. En una recta se tienen los puntos consecutivos A, B, C y D. Si BC = 6 m y
AD = 16 m, hallar la distancia entre los puntos medios de AB y CD .

A) 8 m B) 9 m C) 10 m D) 11 m E) 12 m

Resolución

2a + 6 + 2b = 16 a+b=5 MN = a + 6 + b
∴ MN = 11m

Clave: D



12. En un recta se tienen los puntos consecutivos A, B, C, D y E.
Si 2AE = 3BD y AC + BD + CE = 45m, hallar AE.

A) 27m B) 23m C) 25m D) 21m E) 29m

Resolución

AC + CE + BD = 45 AE + BD = 45
2 AE
AE + = 45 ∴ AE = 27m
3

Clave: A

13. Sean los ángulos consecutivos AOB, BOC, COD y DOE cuyas medidas están en
relación de 1, 2, 3 y 4 respectivamente. Si AOE es llano, hallar el suplemento del
complemento del mayor ángulo.

A) 108º B) 110º C) 162º D) 114º E) 118º

Resolución

10α = 180 α = 18°

SC4α = SC 72° =162°

Clave: C



14. Se tienen los ángulos consecutivos AOQ, QOB y BOC, OQ es bisectriz del ángulo
AOC. Si mAOB - mBOC=40°, hallar la mBOQ.

A) 10º B) 20º C) 15º D) 25º E) 30º

Resolución

2x + α – α = 40°

∴ x = 20°

Clave: B



Geometría
EJERCICIOS DE EVALUACIÓN Nº 01

1. En una recta se tienen los puntos consecutivos A, B, C y D tal que AC = BD y
numéricamente AD = AB(10 – CD). Hallar el mayor valor de BC en metros.

A) 12 m B) 16 m C) 10 m D) 9 m E) 15 m

Resolución

X + 2a = a(10 – a) x= 8a – a2 x = 16 – (a – 4)2

Para X mayor ⇒ a = 4 ∴X = 16m

Clave: B

2. En una recta se tienen los puntos consecutivos A, B, C, D y E.
Si AC + BD + CE = 36m, AE = 24m y DE = 2AB, hallar AB.

A) 3 m B) 5 m C) 6 m D) 4 m E) 8 m

Resolución

AC + CE + BD = 36 AE + BD = 36 BD = 12

3x + 12 = 24 ∴x = 4

Clave: D



3. En una recta se tienen los puntos consecutivos A, B, C y D. Si 3AB=2BC,
AD=96m y CD = AB + AC, hallar BC.

A) 21 m B) 28 m C) 56 m D) 40 m E) 24 m

Resolución

12a = 96 a=8

BC = 3a ∴ BC = 24

Clave: E

4. Sean los ángulos consecutivos AOB, BOC y COD; mAOB = 5mCOD y mBOC =
72º. Si los rayos OA y OD son opuestos, hallar la medida del ángulo formado por las
bisectrices de los ángulos AOB y BOC.

A) 81º B) 71º C) 79º D) 82º E) 80º

Resolución
5α + 72 + α = 180°

α = 18°

x = 45° + 36°

∴ x = 81°

Clave: A



5. Se tienen los ángulos consecutivos AOB, BOC y COD, se traza OX bisectriz del
AOB, OY bisectriz del COD, OP bisectriz del AOY y OQ bisectriz del XOD.
Si mAOD=150° y mBOC=70°. Hallar mPOQ.

A) 30º B) 25º C) 20º D) 22º E) 18º
Resolución

2α + 2β = 80°

2α + =x+β+θ

2β + θ = x + α +

X = (α + β)/2

∴ x = 20°
Clave: C

6 El complemento de un ángulo es igual al suplemento de otro ángulo. Si la suma de
las medidas de dichos ángulos es 130°, hallar la medida del menor ángulo.

A) 30º B) 50º C) 40º D) 20° E) 25º

Resolución

Cα = Sβ 90° - α = 180° - β β - α = 90 …..I

α + β = 130 …. II De I y II : α = 20°

Clave: D




Trigonometría
EJERCICIOS DE LA SEMANA Nº 1

xπ
1. En el gráfico, m BOA = 120° y α = (40 – 7x)g, β = rad . Hallar el valor de
120
x+5.

A) 7

B) 6

C) 3

D) 5

E) 4

Solución:

1º β − α = 120 º

x.180 º 9º
− ( 40 − 7 x ). = 120 º
120 10
3x 63 x
− 36 + = 120
2 10
78x = 152.10
x = 20

2º x+5 =5

Clave: D

2. Un ángulo mide a y b minutos sexagesimales y centesimales, respectivamente. Si
2a 3b
+ = 260 , hallar su medida en radianes.
27 250

3π π π 2π π
A) rad B) rad C) rad D) rad E) rad
5 6 4 5 3



Solución:
a b
1º = = k → {a = 27k, b = 50k
27 50
3k
2º 2k + = 260 → k = 100
5
π
3º a' = 2700' = rad
4
Clave: C

xπ
3. Los ángulos de un triángulo miden (6x)°, (10x)g y rad . Hallar el valor de x.
3

12 12
A) π B) 2,5 C) D) 2,4 E)
51 7

Solución:
xπ
(6 x )º+(10 x )g + rad = 180º
3
9º
(6 x )º +(10 x )g × + (60 x )º = 180 º
10 g
M 75 x = 180
M x = 2,4

Clave: D

4. En la figura, O es un punto de la recta L. ¿Cuál es el valor de x?
L
A) 20

B) 12 (7x-7)°
O
C) 10

D) 8
g
(2x+10)
E) 15

Solución:

1º (2x + 10)g + (7x − 7)º = 90º
9
(2x + 10). + 7 x − 7 = 90
10
9x
+ 7 x = 88
5
x = 10
Clave: C



5. Las medidas de los ángulos α, β y ω son a rad, b° y cg respectivamente, donde
a, b y c están en progresión aritmética. Si b es el cuádruplo de a y a + b + c = 24,
calcular la suma de las medidas de β y ω, en radianes.

π 49π π π 103π
9 450 10 11 900

Solución:
1º a = α – r, b = α, c = α + r
2º 3α = 24 ⇒ α = 8
3º α = 4(α – r) ⇒ r = 6
103° π rad 103π rad
4º β + ω = 8° + 14g = × ⇒ β+ω=
5 180° 900
Clave: E

6. Si a y b son las medidas de un ángulo en minutos, en los sistemas sexagesimal y
a + 2b 42
centesimal, respectivamente, hallar el valor de + .
2a − b 4

13 12 14 9 7
A) B) C) D) E)
2 3 9 14 12

Solución:
a b ⎧a = 27k
1º = =k ⇒ ⎨
27 50 ⎩b = 50k

a + 2b 42 127 42 169 13
2º + = + = =
2a − b 4 4 4 4 2
Clave: A

7. Los ángulos α y β miden 30° y 50g, respectivamente. Hallar la medida de α + β en un
nuevo sistema cuya unidad de medida (1)u corresponde a las tres cuartas partes del
ángulo de una vuelta.

u u u u u
⎛ 11 ⎞ ⎛ 18 ⎞ ⎛ 7 ⎞ ⎛ 18 ⎞ ⎛ 5 ⎞
A) ⎜ ⎟ B) ⎜ ⎟ C) ⎜ ⎟ D) ⎜ ⎟ E) ⎜ ⎟
⎝ 18 ⎠ ⎝ 7 ⎠ ⎝ 18 ⎠ ⎝ 5 ⎠ ⎝ 18 ⎠

Solución:
1º α + β = 30° + 5 × 10g = 30° + 45° = 75°
3
2º 1u = (360°) ⇒ 1u = 270°
4



u
1u ⎛ 5 ⎞
3º α + β = 75° × =⎜ ⎟
270° ⎝ 18 ⎠
Clave: E

8. De acuerdo a la figura, hallar x.

13π
A)
36 −150º
13π L
B) –
36 g O
950
15π 9
C)
36
x rad
15π
D) –
36
π
E) –
3

Solución:
g
⎛ 950 ⎞
• ⎜ ⎟ = 30° – x rad
⎝ 9 ⎠
950 9 180
× = 30 – x ·
9 10 π
180 x
= – 65
π
13π
x=–
36
Clave: B

9. La suma de las medida de dos ángulos es 29°7′30″. Si uno de ellos mide 25g, hallar
la medida del otro en el sistema sexagesimal.

A) 6°25′45″ B) 5°37′30″ C) 4°30′37″
D) 6°37′30″ E) 5°28′36″

Solución:
1º α + β = 29°7′30″
9°
2º β = 25g × = 22°30′
10 g
3º α = 29°7′30″ – 22°30′ = 6°37′30″
Clave: D



10. La medida de un ángulo en el sistema sexagesimal y centesimal es a′ y bm respecti-
vamente. Si b – a = 1 840, hallar la medida del ángulo en radianes.

2π π π π π
3 4 7 5 3

Solución:
a b ⎧a = 27k
1º a′ = bm → = =k ⇒ ⎨
27 50 ⎩b = 50k

2º Luego 23k = 1840 ⇒ k = 80
27.80
R π
3º a′ = 27 · 80′ ⇒ 60 = ⇒ R = rad
180 π 5
Clave: D




Trigonometría
EVALUACIÓN Nº 1

1 720
1. Un ángulo mide S°, Cg y R rad. Si = , calcular la medida de su com-
1 1 C2 − S 2
+
S C
plemento en radianes.

π π π 2π 3π
5 10 4 5 10

Solución:

S C ⎧ S = 9k
1º = =k ⇒ ⎨
9 10 ⎩ C = 10k

90 k 2 720
2º = ⇒ k=2
19 k 19 k 2

π rad
3º S° = 18 ⇒ Comp.(18°) = 72° ×
100°
2π
= rad
5
Clave: D

2. Un ángulo de medida positiva mide S°, Cg y R rad , siendo S y C números ente-
2
⎛S C⎞ 20 R
ros y se cumple que ⎜ − ⎟ − > 0 . Hallar la mínima medida en radianes que
⎝3 5⎠ π
puede tomar el ángulo.

π π π π π
2 10 4 5 20



Solución:
⎧ S = 9k
⎪
S C 20k ⎪C = 10k
1º = = =k >0 ⇒ ⎨
9 10 π ⎪ πk
⎪R =
⎩ 20
2
2º (3k – 2k) – k > 0
k(k – 1) > 0 ⇒ k > 2 ⇒ k = 2
π
3º S° = 18° = rad
10
Clave: B

40
3. Con los datos de la figura y sabiendo que x – y = , calcular el valor de
3
181z + x – 270y.
(z−
A) 53
x)
π ra
30°
d

B) 50
(x+y) g
C) 45
O
D) 52 (3y+z)°

E) 48

Solución:
9°
1º 60° = (x + y)g · ⇒ 3x + 3y = 200
10 g
3x – 3y = 40
x = 40
3y = 80

2º (z – x)π rad + (3y + z)° = 90°
181z = 7210

3º 181z + x – 270y = 7250 – 7250
= 50
Clave: B

4. Sean S° y Cg las medidas de un ángulo en grados sexagesimales y centesimales
respectivamente, tal que 19(C – S) = 360. Hallar la medida del ángulo en radianes.

π 2π 3π π π
4 5 4 10 5



Solución:
S C ⎧S = 9k
1º = =k ⇒ ⎨
9 10 ⎩C = 10k

360 × 19k 2
2º 19k = ⇒k=4
90k 2
π rad
3º S° = 36° =
5
Clave: E

5. Si S y C son los números de grados sexagesimales y centesimales de un mismo án-
⎛S⎞
20 ⎜ ⎟
9 ⎛ S ⎞ ⎝C⎠
gulo, hallar el valor de ⎜ ⎟ .
⎝C⎠

A) 0,83 B) 0,82 C) 0,81 D) 0,91 E) 0,71

Solución:
⎛ 9 ⎞
20 ⎜ ⎟ 18 2
9 ⎛ 9 ⎞ ⎝ 10 ⎠ ⎛ 9 ⎞ ⎛ 9 ⎞ 81
⎜ ⎟ = 9 ⎜ ⎟ =⎜ ⎟ = = 0,81
⎝ 10 ⎠ ⎝ 10 ⎠ ⎝ 10 ⎠ 100
Clave: C




Lenguaje

1. La comunicación humana es…

A) de carácter psíquico, exclusivo del emisor.
B) una actividad mental realizada por el lector.
C) un proceso más sofisticado que en otras especies.
D) una habilidad basada solo en la escritura.
E) de carácter exclusivamente oral

Clave: “C”. La comunicación es un proceso de intercambio de información, en el
caso de los seres humanos. El proceso es más complejo tanto por los elementos
que intervienen como por las reglas que operan, es decir, es un proceso muy sofisti-
cado.

2. Cuando el elemento “receptor” destaca en la comunicación, la función del len-
guaje se denomina…

A) fática o de contacto. B) poética o estética. C) expresiva o emotiva.
D) apelativa o conativa. E) metalingüística.

Clave: D) Cuando se apela a la respuesta del receptor con una pregunta, una or-
den, o un pedido, la función del lenguaje se denomina apelativa o conativa.

3. En el enunciado “Carlos, sentado en el consultorio, escuchaba atentamente
las recomendaciones del médico”, los elementos de la comunicación que se
evidencian son

A) situación, emisor, receptor, y código.
B) emisor, contexto, referente y mensaje.
C) receptor, mensaje, situación y emisor.
D) emisor, código, contexto y canal.
E) receptor, situación, mensaje y emisor.

Clave: “E”. Carlos es el receptor; el consultorio, la situación; las recomendacio-
nes, el mensaje y el médico, emisor.

4. Marque la alternativa que presenta un ejemplo de comunicación humana ver-
bal escrita.

A) La exposición fotográfica en una galería.
B) Las pinturas rupestres en las cuevas.
C) La lectura de un libro sobre Literatura Universal.
D) La entrevista a un grupo de postulantes.
E) Las señales de tránsito en las calles.



Clave: “C” En la biblioteca, se lee documentos para buscar información, por tanto,
la comunicación es verbal escrita.

5. Señale la alternativa en la cual el enunciado destaca la función apelativa del
lenguaje.

A) Ellos encontraron la dirección. B) ¡Qué hermoso paisaje!
C) Se va el barco. D) Eleven su autoestima, jóvenes.
E) La lengua es un sistema abstracto.

Clave: D) La función apelativa se cumple cuando el mensaje buscas una respuesta
o reacción del receptor.

6. En el enunciado “esa señal de tránsito indica que no debemos detenernos”,
predomina la función del lenguaje denominada

A) fática o de contacto. B) apelativa o conativa.
C) representativa o denotativa. * D) expresiva o emotiva.
E) estética o poética.

Clave: “C”. Predomina la función representativa porque el mensaje contiene infor-
mación objetiva, real.

7. Señale la alternativa en la cual se registra la secuencia correcta de la relación
entre las expresiones y las clases de comunicación de las columnas que si-
guen.

a) El rugido de un león ( ….) No verbal visual
b) Una tarjeta de visita ( ….) Verbal oral
c) Las luces del semáforo ( ….) No humana
d) Un concierto instrumental ( ….) Verbal escrita
e) La declamación de un poema ( ….) No verbal auditivo

A) a, c, e, d, b B) d, a, b, e, c C) a, e, d. c, b
D) b, c, e, a, d E) c, e, a, b, d

Clave: “E”

8. Los gestos que utiliza un árbitro en un partido de fútbol constituyen un tipo
de comunicación

A) verbal visual. B) no verbal gestual.* C) verbal visuográfica.
D) no verbal acústica. E) verbal oral.

Clave: “B”. Un árbitro utiliza el movimiento de los brazos y manos para comunicarse
con los jugadores sin articular ninguna palabra.

9. Marque el enunciado conceptualmente correcto.

A) Se denomina idioma a toda lengua que tiene escritura.
B) Solamente el castellano es considerado idioma oficial del Perú.



C) En el Perú, solo existen dialectos regionales bien diferenciados
D) Las sociedades ágrafas carecen de comunicación escrita.*
E) El español que se habla en Piura es un dialecto estándar del norte.

Clave: “D”. Las sociedades “ágrafas” o sin escritura desarrollan básicamente la co-
municación oral,

10. Señale la opción en la que el enunciado cumple la función representativa del
lenguaje.

A) Todos, acérquense inmediatamente.
B) ¡Qué buenas son esas obras de teatro!
C) La sintaxis es un componente de la gramática.
D) Algunos jugadores fueron sancionados.
E) La fórmula del agua es H2O.*

Clave: “E”. En el enunciado “la fórmula del agua es H2O”, comunica de modo obje-
tivo cómo es la composición del agua.

11. Son características de la lengua:

A) innata, universal e invariable. B) articulada y física.
C) social y variable.* D) individual y momentánea.
E) limitante e individual.

Clave: C) Entre otras características, la lengua es social, pertenece a una comuni-
dad; y es variable, ya que presenta diversos dialectos.

12. Marque la alternativa que corresponde a la relación correcta entre los enuncia-
dos de la columna izquierda con las funciones del lenguaje expresadas en la
columna de la derecha.

a) ¡Qué alivio, ya no hay ruido! ( ) apelativa.
b) Irma, la universidad está cerrada. ( ) poética
c) “Dulce voz cual flecha de luz” ( ) metalingüística.
d) Algunas consonantes son sordas. ( ) representativa
e) Regrese pronto, señorita. ( ) expresiva

A) e, c, d, b, a * B) e, a, b, d, c, C) b. e, a, d, c
D) c, d, e, a, b E) a, b, e, c, d

Clave: “A”

13. Señale el enunciado conceptualmente correcto.

A) Las lenguas se concretizan mediante el lenguaje.
B) Las lenguas naturales jamás sufren cambios.
C) La mayoría de lenguas carecen de dialectos.
D) Todas las lenguas presentan cambios históricos.
E) Hay pocas lenguas que presentan dialectos,



Clave: “D”. Todas las lenguas evolucionan, por tanto, presentan cambios históri-
cos.

14. Lengua y habla se caracterizan, respectivamente, por ser

A) concreto y abstracto. B) individual y acústico. C) social y general.
D) abstracto y concreto. E) innato e histórico.

Clave: “D” La lengua se define como un sistema abstracto, mientras que el habla,
como concreto.

15. Señale la alternativa que no corresponde al dialecto estándar del castellano.

A) Los niños juegan muy felices en el parque.
B) Debes actuar con principios y respeto a otros.
C) Los seres humanos gozan de la facultad del lenguaje.
D) Tu fiesta fue bacán, pero nos palteamos con tu yunta.
E) En el primer grado de primaria se aprende a escribir.

Clave: D) En el enunciado se presentan ciertas palabras cuyo uso corresponde a un
lenguaje juvenil y/o sub-estándar..

16. La variedad que se utiliza en la educación y en la administración pública es
conocida como

A) dialecto de la Costa. B) habla de congresistas. C) dialecto estándar.
D) habla de magistrados. E) lengua oficial.

Clave: C) El llamado dialecto estándar es la variedad oficial que se usa en esos ni-
veles sociales.

17. Relacione los enunciados de la columna izquierda con las funciones correspon-
dientes de la columna derecha.

Clave
1. Tome asiento, señor. ____ F. Metalingüística (4)
2. Caral es más antigua que Lima. ____ F. Fática (3)
3. ¿Aló? ¿Sí? ¿Estás ahí? ¿Me escuchas? ____ F. Conativa (1)
4. Las vocales son fonemas sonoros. ____ F. Denotativa (2)
5. Quisiera viajar a Europa. ____ F. Expresiva (5)

18. Seleccione la opción conceptualmente correcta.

A) El lenguaje es un sistema abstracto de signos lingüísticos.
B) El concepto de idioma corresponde al de la lengua oficial. *
C) El dialecto estándar corresponde a una variedad regional.
D) El habla se encuentra en un proceso de constante evolución.
E) Dialecto es un término usado solamente de modo peyorativo.

Clave “B”. Idioma es la lengua que por criterios socio-políticos se define como len-
gua oficial.



19. El elemento de la comunicación que destaca en la función poética es

A) el receptor. B) el emisor. C) el mensaje.
D) el código. E) el canal.

CLAVE: C. El mensaje es el elemento que destaca en la función poética del lengua-
je.

20. Escriba, a la derecha de los enunciados, los elementos de la comunicación
que destacan en cada uno de ellos.

A) El reloj que quieres cuesta caro. ____________________
B) Escucha con más atención. ____________________
C) La lengua es psíquica. ____________________
D) “El mundo es mi casa; el cielo, mi techo”. ____________________
E) Este, o sea, ¿verdad?, ah, ... ____________________
F) ¡Horrible olor, no lo soporto! ____________________
G) ¿Quién está preparado para la competencia? ____________________
H) Los nidos tienen nuevos polluelos. ____________________

CLAVE: A) Referente B) Receptor C) Código D) Mensaje
E) Canal F) Emisor G) Receptor H) Referente

21. Escriba a la derecha de cada concepto si corresponde a lenguaje, lengua,
dialecto, habla o idioma,

A) Sistema lingüístico oficial de un país __________________
B) Uso concreto de la lengua __________________
C) Variedad de la lengua __________________
D) Sistema abstracto, dinámico __________________
E) No es aprendido ni olvidado. __________________
F) Entidad psicofísica e individual __________________
G) Cambia a través de la historia. __________________

CLAVE: A) Idioma B) Habla C) Dialecto D) Lengua E) Lenguaje
F) Habla G) Lengua

22. En el enunciado « a Rosa le preguntó su tía: ‘Hija, ¿qué vestido quieres?’», el
referente es

A) ” su tía”. B) “la pregunta”. C) “Rosa”.
D) “el vestido”. E) “lo respuesta”.



CLAVE: D. El referente es de lo que pregunta la tía de Rosa “el vestido”.

23. Elija la alternativa que corresponde a las siguientes características del lengua-
je: “ es la facultad propia de todos los seres humanos” y “no cambia, mientras
que la especie humana no cambia”.

A) innato – limitante B) individual – limitante
C) universal – inmutable * D) cambiante – social
E) inmutable – innato

CLAVE: C. El lenguaje se caracteriza por ser universal, ya que es propio de to-
dos los miembros de la especie humana y es inmutable porque como facultad del ser
humano no cambia a no ser que la especie humana cambie.

24. En el enunciado “la enfermera me indicó en la sala que debo tomar los medi-
camentos mañana”, los elementos receptor y circunstancia son respectivamen-
te

A) yo y la sala. B) la enfermera y mañana. C) la enfermera y yo.
D) los medicamentos y la sala. E) yo y mañana.

Clave: A. El receptor es la primera persona “yo” y la circunstancia es “la sala” donde
se realizó la comunicación.

25. Señale la oración en la cual destaca la función apelativa.

A) No seas impaciente, Yolanda.
B) Qué bonito vestido luce Diana.
C) Queremos visitar esa ciudad.
D) Es un acuerdo inteligente, señores.
E) Los estrenos son caros en el cine.

CLAVE: “A”. En la oración “no seas impaciente, Yolanda” destaca la función apela-
tiva, ya que se apela al receptor (Yolanda) para que no sea impaciente.

Uso de sin vergüenza y sinvergüenza

Separadas: Preposición “sin” + sustantivo “vergüenza”

Aquellas personas actuaron sin vergüenza

Sinvergüenza: adj. Pícaro, bribón. Ú.t.c.s. || 2. Dícese de las personas que co-
meten actos ilegales en provecho propio, o que incurren en inmoralidades
Ú.t.c.s.

Aquellas personas sinvergüenzas fueron rechazadas.
Aquellos sinvergüenzas serán sancionados.



26. Complete los espacios con la forma adecuada: sin vergüenza o sinvergüenza
Clave
1. Ellos comenzaron a gritar ____________________ (sin vergüenza)
2. No habrá un ________________ que no sea castigado. (sinvergüenza)
3. Ya no cambiará, siempre será un viejito ___________ . (sinvergüenza)
4. Si de un _____________se habla, aquel es el más inmoral. (sinvergüenza)
5. Vamos, hermano, declama, ___________ . (sin vergüenza)
6. Di la verdad, con coraje y _______________. (sin vergüenza)

27. Complete el diagrama de la clasificación del sistema de comunicación y resuelva el
ejercicio que se plantea después.

CLASES

__________ HUMANA

A N IM A L E S ____________ NO VERBAL
V E G E TA L E S ( L IN G Ü Í S T IC A ) _ _ _ _ _ _ _ _ _ _ _ _ __ _

C Ó D IG O C Ó D IG O C Ó D IG O

C o lo re s O ra l E s c r i to V is u a l :_ _ _ _ _ _ _ _ _ _ _ _ _ _
C a n to s ( ) A u d itivo :_ _ _ _ _ _ _ _ _ _ _ _ _ _
T e m p e ra tu ra c o rp o ra l T á c til :_ _ _ _ _ _ _ _ _ _ _ _ _ _
O lo re s Q u í m ic o :_ _ _ _ _ _ _ _ _ _ _ _ _ _

Clave.

C LA S E S

N O H UMANA H UMANA

AN IM A LE S V ER B AL N O V ER B AL
V E GE TA L E S (L I N G Ü Í S T I C A ) (N O L I N G Ü Í S T I C A )

C Ó D IG O C Ó D IG O C Ó D IG O

C ol or es O r al E s c r it o V i s ua l :_ _g e s tos _ __ _ __ _ __ _ __
C a n tos (v is u o g r á f ic o ) A u d it iv o : _ _ _ s ilb id o _ _ _ _ _ _ _ _ _ _ _
T e m p e r a t u ra c o r p o ra l T ác ti l : _ te m p e ra t u r a _ _ _ _ _ _ _ _
O lo re s Q u ím i c o : _ _ _ o lo re s _ _ _ _ _ _ _ _ _ _ _



28. Observe la relación y señale correcto ( C ) o incorrecto ( I ).

Situación Tipo de comunicación
A) Una amiga recibe una carta. Lingüística oral ( I )
B) Percibes el olor del perfume de tu amiga. No lingüística química ( C )
C) El canto de las aves. No humana sonora ( C )
D) Tu madre te da un abrazo. No lingüística visual ( I )
E) Las señas de los mimos. No lingüística gestual ( C )
F) Las señales de tránsito No humana visual ( I )

Clave A-I, B-C, C-C, D-I, E-C, F-I

29. Señale los elementos de comunicación en las siguientes situaciones.

A) José Luis se levanta y saluda a su madre: “Buenos días mamá”.
B) Ernesto, el joven francés, conecta su agenda electrónica que le recuerda que hoy
hay examen.
C) José Luis va a la habitación de su hermana María y le dice: "Ya son las diez".
D) María, la profesora, llega al salón de clase y pide a sus alumnas que escriban
una carta.
E) El conductor no vio la señal de tránsito que indicaba que estaba prohibido esta-
cionarse.

Emisor Receptor Referente Código Canal
A
B
C
D
E

Claves
Emisor Receptor Referente Código Canal
A José Luis su madre saludo castellano ondas sono-
ras
B Ernesto Ernesto el examen francés agenda elec-
trónica
C José Luis María la hora castellano ondas sono-
ras
D María alumnas la carta castellano ondas sono-
ras
E responsables de conductor la prohibición señal de afiche, pan-
las señales tránsi- carta,
to panel




Literatura
SEMANA N° 1

SUMARIO
Literatura. Conceptos básicos. El circuito de la comunicación
literaria. Géneros: épico, dramático, lírico. Figuras literarias:
metáfora, anáfora, epíteto, hipérbaton, hipérbole.
Literatura griega: Ilíada y Odisea.

LITERATURA
La literatura es un hecho cultural muy complejo, tan complejo como es la misma comuni-
cación humana. Funciona en el interior de un contexto sociocultural.

CONTEXTO
(Mundo representado)

EMISOR MENSAJE RECEPTORES
(Autor) (Significado de la obra) (Oyentes o lecto-
res)

CÓDIGO
(Lengua o idioma)

MEDIO O CANAL
(Escritura u oralidad)



LOS GÉNEROS LITERARIOS

Son formas institucionalizadas que agrupan a las obras por sus características comunes.
Tradicionalmente se distinguen tres géneros:
ÉPICO LÍRICO DRAMÁTICO
Es esencialmente narra- El autor se manifiesta Es la representación de acciones a
tivo, alternado con des- desde su mundo interior. través del diálogo y movimiento de
cripciones de lugares y los personajes.
objetos.
Objetivo Subjetivo Subjetivo-Objetivo

FIGURAS LITERARIAS IMPORTANTES

FIGURA DEFINICIÓN EJEMPLO
a) “a” sustituye a “b” Las estrellas de tu rostro. (estrellas = ojos)
Metáfora
b) “a” es “b” Tus ojos son dos estrellas.
Repite una o más pala- No perdono a la muerte enamorada
Anáfora bras al principio de cada no perdono a la vida desatenta
verso u oración. no perdono a la tierra ni a la nada
Adjetivo o participio cuyo La dulce miel de tus ojos; el astuto Odiseo; la
fin es caracterizar. risueña Afrodita; Héctor, domador de caballos;
Epíteto
la sagrada Troya; el divino Aquiles; Hera, la
diosa de los níveos brazos.
Es la alteración del orden Volverán las oscuras golondrinas
Hipérbaton sintáctico normal en la en tu balcón sus nidos a colgar.
oración.
Es la exageración aumen- ¡Oh, más dura que mármol a mis quejas,
tando o disminuyendo ex- y al encendido fuego en que me quemo;
Hipérbole
cesivamente aquello de lo más helada que nieve, Galatea!
que se habla.



LITERATURA UNIVERSAL

LITERATURA GRIEGA

Importante influencia en la literatura universal.

Carácter formativo

Características
Las artes, la filosofía, la historia, la retórica, etc.,
debido a su calidad formal, se han convertido en
verdaderos modelos universales.

Sus formas se han originado en sus propias
instituciones sociales y culturales.

ÉPICA GRIEGA
Destacan dos textos muy antiguos atribuidos a un solo poeta: Homero.

Poemas homéricos
- Epopeyas heroicas compuestas para oyentes alrededor de los siglos IX y VIII a.C.
- Su objetivo es celebrar una Edad Heroica.
- Tienen como fondo común la guerra de Troya.
- Pertenecen a un mundo aristocrático y señorial que tiene su ideal en el pasado.
- Ambas se componen de 24 cantos. Métrica: el hexámetro. Figura literaria: el epíteto.
ILIADA ODISEA
Tema: La cólera de Aquiles y sus fu- Tema: El retorno de Odiseo. El amor a la familia
nestas consecuencias. y a la patria.
Personajes Principales: Personajes Principales:
Griegos: Menelao, Aquiles, Agame- Odiseo, Telémaco, Penélope, los pretendientes,
nón, Néstor, Odiseo, Áyax, Patroclo, el cíclope Polifemo, la hechicera Circe y los dio-
Helena. ses Atenea, Calipso y Poseidón.
Troyanos: Paris, Héctor, Príamo,
Eneas, Sarpedón.
Dioses: Hera, Atenea, Poseidón, Apo-
lo, Artemio, Afrodita.
Comentario: Para Homero, la vida Comentario: Prevalece el mérito de la astucia e
humana es una lucha constante por ingenio del héroe. La inteligencia de Odiseo está
medio de la cual el sujeto alcanza su protegida por Atenea. En esta obra, para Home-
mayor dignidad. Esta epopeya se ro, la vida es un viaje difícil cuyos peligros son
concentra en las proezas humanas de necesarios de afrontar para realizar el destino
seres envueltos en destinos inevita- personal.
bles. Homero presenta el destino de
Troya ligado al destino de Héctor.



EJERCICIOS DE CLASE N° 1

1. El género lírico expresa __________, por ello, podemos decir que es el género más
_________

A) la impersonalidad – objetivo. B) el mundo exterior –dramático.
C) los diálogos – objetivo. D) el tiempo pasado – subjetivo.
E) la emoción personal – subjetivo.

E) El género lírico expresa la emoción personal, el mundo interior: es un género sub-
jetivo.

2. ¿Qué figura literaria se utiliza en los siguientes versos del poeta peruano José María
Eguren?

Y tus ojos
el fantasma de la noche olvidaron,
abiertos a la joven canción.

A) Anáfora B) Símil C) Metáfora
D) Hipérbaton E) Hipérbole

D) Se presenta el hipérbaton, pues el orden sintáctico ha sido cambiado. La sintaxis
normal del verso sería: “Y tus ojos/ abiertos a la joven canción / olvidaron al fantas-
ma de la noche”.

3. ¿Qué figura literaria se ha empleado en los siguientes versos de Miguel de Unamu-
no?

Verde nativo,
verde de yerba que sueña,
verde sencillo,
verde de conciencia humana

A) Hipérbaton B) Epíteto C) Anáfora
D) Metáfora E) Hipérbole

C) La figura literaria que se ha empleado en estos versos es la anáfora que consiste
en la repetición de una o más palabras al inicio de cada verso.

4. En el siguiente fragmento, ¿qué figuras literarias emplea don Quijote de la Mancha
cuando describe a Dulcinea del Toboso?

"Sus cabellos son oro, su frente campos elíseos, sus cejas arcos del cielo, sus ojos
soles, sus mejillas rosas, sus labios corales…"

A) Epíteto e hipérbaton B) Metáfora y anáfora
C) Anáfora e hipérbole D) Hipérbole y epíteto



E) Hipérbaton y metáfora
B) Cervantes emplea las figuras literarias conocidas como metáfora y anáfora. Usa
sobre todo la fórmula metafórica “a” es “b”. La repetición de la forma “sus” al inicio de
cada enunciado determina la presencia de la anáfora.

5. ¿Cuál es la figura literaria empleada por Gabriel García Márquez cuando se refiere
al coronel Aureliano Buendía en el siguiente fragmento de Cien años de soledad?

"Promovió treinta y dos levantamientos armados y los perdió todos. Tuvo diecisiete
hijos varones de diecisiete mujeres distintas, que fueron exterminados uno tras otro
en una sola noche, antes de que el mayor cumpliera treinta y cinco años."

A) Hipérbole B) Metáfora C) Símil
D) Anáfora E) Epíteto

A) La hipérbole está presente a través de los hechos exagerados y fuera de lo coti-
diano que se adjudican a la vida del coronel Aureliano Buendía.

6. Con respecto a la verdad (V) o falsedad (F) de los siguientes enunciados sobre la
Ilíada, marque la alternativa que contiene la secuencia correcta.

I. Aquiles se encoleriza porque Agamenón se apropia de Criseida.
II. Homero describe detalladamente el rapto de Helena por Paris.
III. Esta epopeya tiene como tema central la cólera de Aquiles.
IV. En la obra, los dioses intervienen en la guerra de los hombres.
V. La obra termina con la muerte de Héctor causada por Aquiles.

A) V-F-F-F-V B) V-V-F-F-F C) F-V-F-V-V
D) F-F-V-V-F E) V-F-V-F-V

D) I. Aquiles se encoleriza porque Agamenón se apropia de Briseida. (F)
II. Homero narra la cólera de Aquiles y sus consecuencias. (F)
III. El tema central de la Ilíada es la cólera de Aquiles. (V)
IV. Los dioses intervienen según los bandos en pugna. (V)
V. La Ilíada termina con los funerales de Héctor. (F)

7. Marque la alternativa que contiene solo personajes troyanos de la Ilíada.

A) Menelao, Aquiles, Príamo B) Paris, Héctor, Príamo
C) Aquiles, Héctor, Patroclo D) Odiseo, Príamo, Eneas
E) Áyax, Paris, Agamenón

B) Paris y Héctor son príncipes troyanos protagonistas de la Ilíada al igual que el
héroe Eneas, hijo del noble troyano Anquises y de la diosa Afrodita.

8. La muerte de Héctor provocada por Aquiles, en la Ilíada, supone de forma implícita la

A) guerra entre troyanos y aqueos. B) cólera de Aquiles.
C) muerte de Aquiles. D) victoria de los troyanos.
E) destrucción de Troya.



E) La vida de Héctor en la Ilíada, aparece ligada al destino de Troya, su muerte es
un anuncio de la posterior destrucción de esa ciudad.
9. En la Odisea, la diosa que protege a Odiseo es

A) Calipso. B) Circe. C) Atenea. D) Afrodita. E) Hera.

C) La diosa Atenea protege a Odiseo y a su familia durante todo el transcurso del
poema homérico.

10. Marque la alternativa que completa la siguiente expresión: "En la Odisea, el persona-
je principal afronta el difícil viaje de retorno a Ítaca

A) guiado por el deseo de conquistar nuevas tierras".
B) porque los dioses le obligan a regresar pronto".
C) por el profundo amor a su patria y a su familia".
D) porque equivoca el camino a la isla de Ogigia".
E) para huir de la sangrienta guerra de Troya".

C) Odiseo sufre un largo y difícil viaje del retorno a Ítaca motivado por el amor que
siente por su patria y su familia.

11. ¿Qué cualidad caracteriza a Odiseo?

A) La inteligencia B) La fuerza C) El poder
D) La mesura E) El temor

A) La inteligencia caracteriza a Odiseo y le permite superar todas sus adversidades.



Psicologia
PRÁCTICA N° 1

Instrucciones:
Lee atentamente las preguntas y contesta eligiendo la alternativa correcta.

1. Al sentir una superficie áspera con la mano se activa el lóbulo cerebral

A) frontal. B) parietal. C) occipital.
D) temporal. E) límbico.

Solución:
El lóbulo parietal tiene como función a la sensibilidad táctil.
Clave: B

2. Cuando un arquitecto crea la maqueta de un edificio utiliza principalmente el

A) lóbulo temporal. B) hemisferio izquierdo.
C) hemisferio derecho. D) sistema límbico.
E) hipotálamo.

Solución:
El hemisferio derecho es la estructura que se activa en los procesos creativos y que
procesa información espacial.
Clave: C

3. En una situación de peligro como el inminente ataque de un animal salvaje que
provoca el escape inmediato de una persona se activa el

A) tálamo. B) lóbulo frontal.
C) sistema simpático. D) sistema parasimpático.
E) hemisferio izquierdo.

Solución:
El sistema simpático participa en las respuestas de huída ante una situación de
peligro o emergencia.
Clave: C

4. La sensación de hambre que surge después de varias horas sin comer esta
regulada por la estructura denominada

A) hipotálamo. B) tálamo. C) tronco encefálico.
D) límbico. E) occipital.



Solución:
El hipotálamo regula las necesidades básicas como el hambre, la sed y la conducta
sexual.
Clave: A

5. Al realizar una operación lógica para hallar el resultado de una ecuación se activa el.

A) tálamo óptico. B) tronco encefálico. C) cerebelo.
D) hemisferio derecho. E) hemisferio izquierdo.

Solución:
El hemisferio izquierdo está implicado en la ejecución de operaciones lógico
matemáticas.
Clave: E

6. Experimentar miedo al pasar por una calle donde se sufrió la mordida de un perro se
activa la estructura nerviosa denominada

A) tálamo óptico. B) tronco encefálico. C) sistema límbico.
D) hemisferio derecho. E) hipotálamo.

Solución:
El sistema límbico participa en el recuerdo, aprendizaje y experiencias emocionales.
Clave: C

7. Si una persona por comer algo descompuesto presenta vómitos, dicha reacción está
regulada por

A) hemisferio derecho. B) lóbulo frontal.
C) tronco encefálico. D) hemisferio izquierdo.
E) lóbulo temporal.

Solución:
El tronco encefálico regula la reacción de vómito.
Clave: B

8. Si me siento temeroso, pero intento controlarme. Esto se puede lograr gracias a la
acción del hemisferio

A) derecho B) izquierdo. C) límbico.
D) parietal. E) occipital.

Solución:
El hemisferio izquierdo se encarga del controlar racionalmente las emociones.
Clave: B

9. La unidad básica estructural de sistema nervioso es



A) el área de broca. B) el hipotálamo. C) la neurona.
D) el hemisferio cerebral. E) el sistema simpático.

Solución:
La neurona es la unidad básica estructural del sistema nervioso.
Clave: C

10. Cuando una persona levanta la mano para el bus se detenga, se activa el lóbulo

A) parietal. B) temporal. C) frontal.
D) límbico. E) hipotalámico.

Solución:
En el lóbulo frontal se encuentra la corteza motora que controla la ejecución de
movimientos voluntarios.
Clave: C



Historia

1. La ciencia histórica se caracteriza principalmente por

A) realizar un estudio ordenado de la evolución natural.
B) hacer una investigación sistemática en base a fuentes.
C) estudiar científicamente los restos óseos de los primates.
D) elaborar una historia completa de la megafauna primitiva.
E) sintetizar la historia de las capas estatigráficas terrestres.

Rpta B. La Historia es una ciencia que se caracteriza por realizar una investiga-
ción formal, sistemática y ordenada en base a fuentes y su objeto de estudio
es el hombre como ser social.

2. A través del proceso de hominización los antecesores del hombre moderno

1. tuvieron un fuerte aumento del prognatismo.
2. desarrollaron al máximo sus instintos.
3. adoptaron la bipedestación.
4. aumentaron su capacidad craneana.
5. pudieron fabricar y manipular herramientas.

A) 1, 2, 3 B) 2, 3, 4 C) 1, 3, 5 D) 1, 3, 4 E) 3, 4, 5

Rpta E. La hominización es un proceso evolutivo que implica cambios físicos y psí-
quicos como: La adopción de la bipedestación; el caminar erguido; la disminución
del prognatismo (Prognatismo: Cualidad de prognato. Prognato: Dicho de una per-
sona: Que tiene salientes las mandíbulas); la aparición de una grácil mandíbula en
forma de “U”; el aumento de la capacidad craneana, unida a la facultad de visión
cromática y estereoscópica; la manipulación y fabricación de objetos gracias al dedo
pulgar oponible en las manos; y, un comportamiento no instintivo sino supeditado a
una inteligencia muy desarrollada que originó entre otras cosas la aparición del len-
guaje.

3. Fue una consecuencia de la invención de herramientas de piedra, hecha por el
Homo habilis.

A) El progreso en la evolución al obtener una mejor dieta alimenticia.
B) El desarrollo cultural que le permitió desplazarse por Oceanía.
C) La domesticación del fuego para comer alimentos sanos.
D) La exterminación de forma contundente de la megafauna.
E) El impulsar la desaparición total de los Homo sapiens.

Rpta A. La invención de la herramienta hecha por el Homo habilis fue fundamental
para su progreso evolutivo, al obtener la herramienta, le permitió cortar y obtener
más carne, obteniendo así una mejor dieta.



4. El excedente productivo fue fundamental en la economía neolítica porque ini-
ció

A) la domesticación de plantas y animales.
B) la expansión de los primeros imperios.
C) las transacciones monetarias en Oriente.
D) la desaparición de la propiedad privada.
E) los intercambios en base al trueque

Rpta E. Con la generación del excedente productivo la economía neolítica cambió,
ya que se dio inicio al intercambio simple bajo la forma del trueque.

5. Fue una característica política de la Edad del Bronce.

A) Inicio de los gobiernos jefaturales.
B) Desarrollo de la escritura alfabética.
C) Empleo de armas para la guerra.
D) Expansión de los códigos civiles.
E) Apogeo de los estados esclavistas.

Rpta C. En la época del bronce la metalurgia se desarrolla para la fabricación de
armas para la guerra, este hecho fue posible, debido al surgimiento de los estados
militaristas que hacían uso frecuente de la guerra.




Geografía
EJERCICIOS Nº 1

1. El empleo de las coordenadas geográficas permite aplicar el principio de
A) descripción. B) comparación. C) causalidad.
D) relación. E) localización.
Solución:
La aplicación del principio de localización permite ubicar cualquier lugar de la super-
ficie terrestre, para lo cual se recurre a las coordenadas geográficas.
Clave: E
2. Identifica el objeto de estudio de la ciencia geográfica.
A) Espacio geográfico B) La Tierra C) El universo
D) El mundo E) La litósfera
Solución:
Uno de los elementos que permitieron la consolidación científica de la geografía ac-
tual es el establecimiento y definición de su objeto de estudio.
Clave: A
3. Ubica las coordenadas geográficas de los puntos señalados en el planisferio.

A) ________________ B) ________________ C) ________________
D) ________________ E) ________________



Solución:
A) 110° LW, 40° LN B) 50° LW, 30° LS C) 0° L, 10° LN
D) 130° LE, 30° LN E) 150° LE, 40° LS

4. Línea imaginaria trazada sobre la superficie terrestre considerada la de mayor ex-
tensión.
A) Ecuador terrestre B) Trópico de cáncer C) Círculo polar ártico
D) Círculo polar antártico E) Trópico de capricornio

Solución:
Las líneas imaginarias mayores son aquellas que dividen la Tierra en dos partes
iguales: el ecuador terrestre y el meridiano base.
Clave: A

5. Línea imaginaria terrestre que une los polos Norte y Sur.

A) Círculo polar B) Trópico de cáncer C) Línea ecuatorial
D) Meridiano base E) Trópico de capricornio

Solución:
El meridiano base es la línea imaginaria que describe una trayectoria de polo a polo,
pasa por el observatorio de Greenwich en Inglaterra y continua por Francia, Argelia, etc.
Clave: D

6. Línea imaginaria terrestre que se localiza a 66°33′ de distancia del polo Norte.

A) Círculo polar ártico. B) Círculo polar antártico. C) Meridiano base.
D) Trópico de cáncer. E) Trópico de capricornio.

Solución:
El Trópico de cáncer se halla a 23°27′ de latitud norte, es decir a 66°33′ del polo norte.
Clave: D
7. El ____________ es la línea imaginaria que pasa por los territorios de Sudamérica,
África y Australia.

A) Eje terrestre B) Trópico de cáncer C) Círculo polar
D) Meridiano base E) Trópico de capricornio

Solución:
El Trópico de capricornio pasa por los territorios de África, Oceanía y América del
sur. Esta línea imaginaria se localiza a 23° 27′ de LS y sirve de referencia para seña-
lar el solsticio de verano del hemisferio Sur.
Clave: E

8. Los puntos de igual latitud están situados

A) en el hemisferio Norte. B) en el mismo meridiano.
C) a lo largo del meridiano de Greenwich. D) en el mismo paralelo.
E) al Sur del Ecuador.



Solución:
La latitud es la distancia angular de un punto cualquiera con respecto al ecuador te-
rrestre. Los puntos de igual latitud están situados en el mismo paralelo.
Clave: D

9. El equinoccio de otoño se produce en el hemisferio Sur cuando los rayos solares
inciden perpendicularmente en el

A) trópico de capricornio. B) ecuador terrestre. C) círculo polar.
D) eje terrestre. E) antimeridiano.
Solución:
El 21 de marzo los rayos solares caen perpendicularmente sobre la línea ecuatorial,
produciéndose en el hemisferio sur el equinoccio de otoño.
Clave: B

10. La diferencia latitudinal entre Lima (77° LW, 12° LS) y México (99° LW, 19° LN) es de

A) 31° B) 23° C) 87° D) 7° E) 57°

Solución:
La diferencia de latitud entre dos puntos se obtiene sumando los valores de latitud
de cada uno, cuando corresponden a hemisferios diferentes (N, S).
Clave: A

11. ¿Cuál de las siguientes ciudades tiene coordenadas geográficas opuestas a la de
Lima?

A) Sydney B) Quito C) Roma D) Miami E) Lisboa

Solución:
Lima presenta LW y LS, por lo tanto el opuesto será cualquier punto de LE y LN, es decir
ubicado en el primer cuadrante, Roma corresponde al tipo de coordenada opuesta.
Clave: C

12. La diferencia longitudinal entre Lima (77° LW) y la ciudad de Londres es

A) 180° B) 45° C) 70° D) 67° E) 77°

Solución:
La diferencia longitudinal se calcula considerando que si los valores de longitud co-
rresponden a un mismo hemisferio se suman dichos valores.
Clave: E




Filosofía
EVALUACIÓN N° 1

1. Si, en torno a la filosofía, enfatizamos la relación del amor con la sabiduría, es
porque estamos interesados en su

A) origen histórico. B) valor cognoscitivo. C) complejidad.
D) antiguedad. E) etimología.

“E” En torno a la filosofía, en su curso histórico, la unidad de amor y sabiduría ha
estado relacionado en primer lugar a su etimología.

2. Cuando Aristóteles definió a la filosofía como el estudio y el conocimiento de
las primeras causas y primeros principios, puso de relieve su carácter

A) trascendente. B) radical. C) cognoscitivo.
D) intrascendente. E) universal.

“B” Aristóteles en su definición puso de relieve el carácter radical de la filosofía por-
que muestra la búsqueda de los más primero que da origen a las cosas.

3. Si afirmamos que la filosofía es el amor a la sabiduría y luego que es el cono-
cimiento de las primeras causas y los primeros principios, entonces, respecto
de la filosofía, tenemos

A) definición y concepto.
B) definicióny objeto de estudio.
C) etimología y definición.
D) objeto de estudio y fundamentación.
E) fundamentación y proyecto.

“C” Las dos afirmaciones juntas sobre la filosofía muestran tanto su significado eti-
mológico como su definición ya posterior a la etimología.



4. La pregunta sobre si lo bueno es útil o si lo útil es bueno, es decir, si valen,
pertenece al campo de la

.

.

A) heraclitiano confeso. B) defensor de Empédocles.
C) seguidor de Sócrates. D) discípulo de Thales.
E) refutador de Sócrates.

“C” Tanto la mayéutica como la inducción son métodos para conocer asociados his-
tóricamente a Sócrates.

9. Los pre-socráticos enfatizan el estudio ___________, mientras que los socráti-
cos ____________.

A) de las ideas — de la mayéutica. B) del cosmos — del hombre.
C) del principio — de lo secundario. D) del mundo — de la realidad.
E) del hombre — de la naturaleza



10. Si los filósofos sanmarquinos fuesen protagóricos afirmarían que

A) todo en esta vida es relativo.
B) la las normas morales son absolutas.
C) la naturaleza es la medida del hombre.
D) el hombre es solamente un individuo.
E) el conocimiento es absoluto.

“A” A Protágoras está vinculada la tesis de que nada es absoluto sino mas bien
relativo y que el hombre es la medida de todas las cosas.

“La filosofía es el búho de Minerva que levanta su vuelo cuando las sombras
caen”
Hegel

DOCENTES DE SOCIALES 2 (Filosofía-Lógica y Economía)
Aníbal Campos Rodrigo (J. C. de Filosofía), Julio Chávez Rivera (J. C. de Econo-
mía), Wilbert Almonte Prado, Benavides Caldas, Manuel Bermúdez Lizárraga, Ma-
rio Cóndor Salcedo, Carlos Contreras Paz, Hugo Maguiña Molina, Pedro Mascaro
Canales, Eusebio Rodríguez Sánchez, Hugo Rojas Juárez, Carlos Sánchez Pare-
des, Cornelio Ticse Nuñez.




Biología
CIENCIAS BIOLÓGICAS

OBJETO DE ESTUDIO MÉTODO DE ESTUDIO

CARACTERÍSTICAS NIVELES DE DOMINIOS MÉTODO CIENTÍFI-
DE LOS SERES VI- ORGANIZACIÓN CO
VOS • Bioquímica
• Atómico • Biofísica
• Organización • Molecular • Biología celular • Observación
específica • Macromolecular • Histología • Hipótesis
• Movimiento • Subcelular • Embriología • Experimentación
• Irritabilidad y • Celular • Paleontología y resultados
coordinación • Tisular •
• Taxonomía Conclusiones y
• Crecimiento • Organológico teorías
• Ecología
• Adaptación • Sistémico • Virología
• Reproducción • Individual • Bacteriología
• Metabolismo • Población • Protozoología
• Comunidad • Micología
• Ecosistema
• Ecósfera

COMPOSICIÓN DE LA MATERIA VIVA

BIOELEMENTOS

ORGANÓGENOS SECUNDARIOS OLIGOELEMENTOS

PRINCIPIOS INMEDIATOS

INORGÁNICOS ORGÁNICOS
• Agua • Glúcidos
• Oxígeno • Lípidos
• Anhídrido car- • Proteínas
bónico • Ácidos nucleicos
• Sales minerales • Vitaminas




1. La Ciencia que estudia a los organismos cuyos restos se encuentran fosilizados.

A) Paleontología B) Fisiología C) Anatomía
D) Virología E) Ecología

Rpta. “A” La Paleontología es la ciencia que trata de los organismos cuyos restos
se encuentran fosilizados.

2. En la fase experimental del método científico, la condición que distingue al grupo
experimental del control se conoce como

A) factor constante. B) cofactor. C) multifactorial.
D) unifactorial. E) factor variable.

Rpta. “E” La condición que distingue al grupo experimental del grupo control se
conoce como factor variable.

3. Si un organismo logra desarrollar, durante un tiempo, ciertas propiedades estructu-
rales o funcionales que le permiten subsistir, ha logrado

A) reproducirse. B) crecer. C) adaptarse.
D) metabolizar. E) moverse.

Rpta. “C” La adaptación es la facultad de desarrollar, durante un tiempo determina-
do, propiedades estructurales o funcionales que le permiten subsistir y reproducirse
bajo ciertas condiciones.

4. Los cromosomas se encuentran organizados como complejo

A) atómico. B) molecular C) supramolecular
D) macromolecular. E) celular.

Rpta. “C” Los cromosomas se encuentran organizados como complejo supramole-
cular es decir el resultado de la interacción establecida por diferentes macromolécu-
las.

5. El conjunto de poblaciones que habitan en un lugar y un tiempo determinado se
denomina

A) comunidad. B) población. C) ecósfera.
D) biósfera. E) ecosistema.

Rpta. “A” El conjunto de poblaciones que habitan en un lugar y un tiempo determi-
nado se denomina comunidad.



6. El pulmón está formado por la asociación de __________________ por lo que ocu-
pa el nivel _________________.

A) células – celular B) tejidos – organológico
C) sistemas – sistémico D) organelas – organológico
E) moléculas – macromolecular

Rpta. “B” El pulmón está formado por la asociación de tejidos por lo que ocupa el
nivel organológico.

7. Es un principio inmediato inorgánico indispensable para la síntesis de moléculas
orgánicas en la fotosíntesis.

A) Oxígeno B) Sal mineral C) Metano
D) Nitrógeno E) Anhídrido carbónico

Rpta. “E” El anhídrido carbónico es un principio inmediato inorgánico indispensable
para la síntesis de moléculas orgánicas en la fotosíntesis.

8. Los vertebrados poseen en sus articulaciones bolsas de líquido sinovial que evitan
el roce entre los huesos y cumplen una función

A) mecánica – amortiguadora. B) de regulador térmico.
C) de soporte de reacciones. D) humedecer las membranas.
E) de excreción de los desechos.

Rpta. “A” Los vertebrados poseen en sus articulaciones bolsas de líquido que evita
el roce entre los huesos y cumple una función mecánica amortiguadora.

9. Las proteínas presentes en la sangre de los vertebrados que protegen contra sus-
tancias extrañas son denominadas

A) péptidos. B) aminoácidos. C) hormonas.
D) anticuerpos. E) polipéptidos.

Rpta. “D” Las proteínas presentes en la sangre de los vertebrados y que protegen
contra sustancias extrañas son denominadas anticuerpos.

10. La lactasa es una enzima que cataliza

A) la hidrólisis del azúcar de la leche. B) la transferencia de electrones.
C) el almacenaje de caseína. D) el transporte de hemocianina.
E) el metabolismo de la glucosa.

Rpta. “A” La lactasa es una enzima esencial que permite a los organismos degra-
dar la lactosa de la leche en glucosa y galactosa.

11. Es un polisacárido de reserva sintetizado en los animales y en los hongos.

A) Celulosa B) Almidón C) Quitina
D) Colesterol E) Glucógeno



Rpta. “E” El glucógeno es un polisacárido de reserva sintetizado en los animales y
en los hongos.

12. Son lípidos que forman parte estructural de las membranas celulares.

A) Ceras B) Grasas C) Fosfolípidos
D) Vitamina D E) Sales biliares

Rpta. “C” Los fosfolípidos forman parte de las membranas celulares, además de
los glucolípidos.

13. Las ____________ recubren y protegen, principalmente de la humedad, pelos,
plumas, hojas y frutos.

A) sales B) vitaminas C) hormonas
D) ceras E) proteínas

Rpta. “D” Las ceras recubren y protegen, principalmente de la humedad, pelos,
plumas, hojas y frutos.

14. Al hidrolizarse los nucleótidos se descomponen en una base nitrogenada, un ácido
fosfórico y una_____________

A) hexosa. B) pentosa. C) triosa.
D) manosa. E) cetosa.

Rpta. “B” Al hidrolizarse los nucleótidos se descomponen en una base nitrogena-
da, un ácido fosfórico y una pentosa.

15. El ADN se encuentra en el _________ donde interacciona con el ARN ________
A) núcleo - mensajero. B)citoplasma – de transferencia.
C) ribosoma - ribosomal. D) lisosoma – de transferencia.
E) Golgi - mensajero.

Rpta. “A” El ADN se encuentra en el núcleo donde interacciona con el ARN men-
sajero quien interviene en el proceso de transcripción




Física
(Áreas: A, D y E)

1. Si la ecuación A = BC + kRD es dimensionalmente homogénea, siendo B: presión,
C: volumen, D: densidad. Determinar la ecuación dimensional de A.

A) MLT – 2 B) MLT – 1 C) M2LT – 2 D) ML2T – 2 E) MLT

Solución:
[A] = [B] [C] = (ML– 1T –2)(L3) = ML2T –2
Clave: D

2. Indicar la verdad (V) o falsedad (F) de las siguientes proposiciones:

I. Las cantidades trabajo y energía tienen la misma dimensión.
II. La dimensión de la frecuencia es T–1.
III. El análisis dimensional permite verificar la homogeneidad de una ecuación físi-
ca.

A) VVV B) VVF C) VFV D) FVF E) FVV

Solución:
I) V II) V III) V
Clave: C
GMm
3. Hallar la dimensión G en la ecuación F= ; donde F: fuerza, M, m: masas y
R2
R: distancia.

A) MLT–1 B) M–1L3T–2 C) ML3T
D) M–1L2T E) M–2L–1T–2
Solución:

Habilidad Verbal – Semana Nº 1 (Prohibida su reproducción y venta) Pág.
100


FR 2 MLT −2L2
G= ⇒ [G] = = M−1L3 T − 2
Mm 2
M
Clave: B

4. La figura muestra un cuadrado de lado a. Si M y N son los puntos medios de sus
respectivos lados, hallar el módulo de los vectores mostrados en la figura.

A) a 2

B) 2a 2

C) 4a 2

D) 3a 2

a
E) 2
2

Solución:

R=a 2 +a 2

R = 2a 2
Clave: B


I. Dos vectores diferentes pueden tener igual magnitud.

II. Dos vectores son iguales cuando tienen la misma dirección y magnitud.

III. La magnitud de la resultante de dos vectores siempre es mayor que uno de
ellos.

A) VVV B) VVF C) VFV D) FVF E) FVV

Solución:
I) V II) V III) F
Clave: B
6. En la figura mostrada. Hallar el vector resultante
101


A) 0

B) a

C) b

D) 2 a

E) 2 g

Solución:

2g ó 2b

a + c + d + e + f =0
Clave: E
7. Hallar el módulo de la resultante de los vectores A y B mostrados en la figura:

A) 2 cm

B) 2 2 cm

C) 3 2 cm

D) 6 cm

E) 3 cm

Solución:

Rx = 2 cm

Ry = 1 cm

Rz = 1 cm

R2 = (2)2 + (1)2 + (1)2

R2 = 6 ⇒ R = 6 cm
Clave: D

102




Física
(Áreas: B, C y F)


I. En el sistema internacional (SI) la carga eléctrica es una cantidad fundamental.

II. El sistema internacional (SI) consta de siete cantidades fundamentales.

III. Dos cantidades físicas diferentes pueden tener igual dimensión.

A) VVV B) VFV C) FVV D) FVF E) FFV

Solución:
I) F II) V III) V
Clave: B

GMm
2. Hallar la dimensión G en la ecuación F= ; donde F: fuerza, M, m: masas y
R2
R: distancia.

A) MLT–1 B) M–1L3T–2 C) ML3T
D) M–1L2T E) M–2L–1T–2

Solución:

FR 2 MLT −2L2
G= ⇒ [G] = = M−1L3 T − 2
Mm 2
M
Clave: B

103



I. Dos vectores son iguales si tienen la misma magnitud.
II. Dos vectores son iguales si tienen la misma dirección.
III. La magnitud del vector resultante de dos vectores opuestos es cero.

A) VVV B) VFV C) FFV D) FVF E) FFF

Solución:
I) F II) F III) F
Clave: E

4. Hallar la magnitud de la resultante de dos vectores de 15 y 7 unidades que forman
entre si un ángulo de 53°.

A) 20 μ B) 10 μ C) 12 μ D) 15 μ E) 30 μ

Solución:

R= 15 2 + 7 2 + 2(15)(9) cos 53° = 20μ
Clave: A

5. La figura muestra una circunferencia de centro O. Determine el vector x en función
de los vectores a y b .

a − 2b
A) x =
2
b +a
B) x =
2
−b +a
C) x =
2
2b − a
D) x =
2
2a − b
E) x =
2

Solución:

b a a b
x + = ⇒ x = −
2 2 2 2
a −b
x =
2
Clave: A

104


QUÍMICA
“Hay dos razones de peso por las que es preciso
que la sociedad apoye la ciencia básica. Una es
pragmatica : la oscura química sintética de ayer
hoy cura enfermedades; la física teórica de ayer es
la defensa nuclear de hoy. La otra razón es cul-
tural. La esencia de nuestra civilización consiste
en explorar y analizar la naturaleza del hombre y
lo que lo rodea”.

LA QUÍMICA ESTA EN TODAS PARTES
♦ Ya sea que se analicen sustancias en el suelo, en el agua o en el aire
– la QUÍMICA está presente.

♦ Si se desarrollan equipos ligeros para materiales deportivos o nue-
vos materiales semiconductores – la QUÍMICA está presente.

♦ Cuando se trabaja en el desarrollo de nuevos aerosoles que no des-
truyan la capa de ozono o de nuevas sustancias para combatir el si-
da, el cáncer, u otros misterios de la medicina – la QUÍMICA está
presente.

LOS FUNDAMENTOS DE LA QUÍMICA, OCUPAN UN LUGAR EN EL
CENTRO DE TODA CIENCIA, POR LO TANTO LA QUÍMICA ESTÁ
EN TODAS PARTES.

Los profesores del curso esperamos en verdad, que disfrutes tu aven-
tura en el mundo de la QUIMICA. ¡El éxito depende de ti!, recuerda
que el ascenso hacia nuevas alturas puede ser difícil, pero el “paisa-
je que se ve desde las alturas” es fantástico.

105


La Química es la ciencia que estudia la materia, sus propiedades físicas y químicas, los
cambios y transformaciones que experimenta y las variaciones de energía que acompa-
ñan a dicha transformación.

El avance de la química como ciencia sigue el siguiente método científico

PROBLEMA

OBSERVACIÓN

HIPÓTESIS NUEVA
HIPÓTE-

EXPERIMENTACIÓN

TEORÍA

LEY

MAGNITUD: todo aquello que se puede medir y cuantificar

a) Magnitudes básicas. Ejm. La masa
b) Magnitudes derivadas. Ejm. El volumen.

MAGNITUDES Y UNIDADES DEL SISTEMA INTERNACIONAL (SI)

MAGNITUDES Y UNIDADES BÁSICAS MAGNITUDES Y UNIDADES
DERIVADAS
MAGNITUD UNIDAD SÍMBOLO MAGNITUD SÍMBOLO
Masa kilogramo kg Volumen m3
Longitud metro M Densidad kg/m3
Temperatura kelvin K Velocidad m/s
Tiempo segundo s Fuerza kg.m/s2 = 1 N
Intensidad amperio A Área m2
de corriente
Intensidad candela cd Presión N/m2 = 1 Pa
luminosa
Cantidad de mol mol Aceleración m/s2
sustancia

106


Múltiplos
Deca(da) Kilo Mega(M) Giga(G) Tera Peta
(k) (T) (P)
101 103 106 109 1012 1015
Unidad
Base (100)

Submúltiplos
Deci(d) Centi (c) Mili (m) Micro Nano Pico
(μ) (n) (p)
10–1 10–2 10–3 10–6 10–9 10–12

Ejemplo : (submúltiplo) 1 mm = 10–3 m (Múltiplo) 1 Mm = 106 m

NOTACIÓN CIENTÍFICA: 120 000 = 1,2 x 105 y 0,000012 = 1,2 x 10–5

FACTOR DE CONVERSIÓN: Se generan a partir de una igualdad

1 pulgada = 2, 54 cm

1pu lg . 2,54 cm
254 cm x = 100 pulg. 10 pulg. x = 25,4 cm
2,54 cm 1 pu lg .

DENSIDAD : Relación de la masa con el volumen
masa (g) masa (g)
D= o
Volumen (mL o cm 3 ) Volumen (L )
para sólidos o líquidos para gases

VALORES DE LA DENSIDAD PARA ALGUNAS SUSTANCIAS

Sólidos g/cm3
Oro 19,30
Plomo 11,30
Aluminio 2,70
Hierro 7,86
Cobre 8,92
Sal de mesa 2,16
Líquidos g / mL
Agua pura 0,998
Agua de mar 1,03
Mercurio 13,6
Gases g/L
Aire 1,29
Oxígeno 1,43
Dióxido de carbono 1,96

107


SEMANA Nº 1 MAGNITUDES, UNIDADES, CONVERSIONES Y DENSIDAD

1. La Química como toda Ciencia, está constituida por un conjunto de conocimientos.
Indique las etapas para alcanzar los dos grandes conocimientos en Química, indi-
cadas en el gráfico.

Teoría Atómica

(I) (II) (III)
Ley de Lavoisier

A) Experimentación, hipótesis. Aplicación B) Observación, aplicación, hipótesis
C) Observación, hipótesis, experimentación D) Observación, hipótesis, aplicación
E) Hipótesis, observación, experimentación.

Solución:
Teoría Atómica

OBSERVACION HIPOTESIS EXPERIMENTACIÓN
Ley de Lavoisier

Rpta. C
2. Marque la secuencia correcta de verdadero (V) o falso (F):

I. Las propiedades del elemento nitrógeno es estudiada por la Química Orgánica.
II. El tiempo de vigencia de un fármaco es estudiado por la Química Inorgánica.
II. La cantidad de hierro en la sangre es determinada por la Bioquímica.
IV. El proceso de respiración de las plantas es estudiada por la Fisicoquímica.

A) FFFF B) FVVF C) VVVF D) VVFV E) VVVV

Solución:

I. FALSO: Las propiedades del elemento nitrógeno, así como los restantes ele-
mentos químicos es estudiada por la Química Inorgánica.
II. FALSO: El tiempo de vigencia de un fármaco es estudiado por la FISICOQUI-
MICA, específicamente en Cinética Química.

III. FALSO: La cantidad de hierro en la sangre, o cualquier elemento en cualquier
tipo de materia es determinada por Química Analítica

IV. FALSO: Los procesos químicos que involucran a los seres vivos es estudiado
por la BIOQUIMICA.

Rpta. A

108


3. Complete el siguiente cuadro con Magnitudes y Unidades Básicas del sistema inter-
nacional (S.I.).

Magnitud Unidad
Cantidad de
(I)
sustancia
(II) Amperios (A)
(III) Kelvin (K)
Longitud (IV)

A) Kilogramo (kg), Intensidad de corriente, temperatura, kilometro (km).
B) Mol (mol), carga de corriente eléctrica, temperatura, metro (m).
C) Kilogramo (kg), Intensidad de corriente, Intensidad luminosa, metro(m).
D) Gramo (g), Intensidad de corriente, intensidad luminosa, kilometro (km).
E) Mol (mol), Intensidad de corriente, temperatura, metro (m).

Solución:

Magnitud Unidad
Cantidad de
mol(mol)
sustancia
Intensidad de
Amperios (A)
corriente
Temperatura Kelvin (K)
Longitud metro (m)

Rpta. E

4. Indique el número de magnitudes básicas y magnitudes derivadas, respectivamente,
en la siguiente descripción:
“Dos moles de gas helio tienen una masa de 8,0 g. A condiciones normales, es decir
1,013 x 105 Pa y 273 K, ocupan un volumen de 44,8 L”

A) 2 y 3 B) 3 y 1 C) 2 y 2 D) 3 y 2 E) 4 y 1

Solución:

Magnitud Básica: Magnitud Derivada:
1. Cantidad de sustancia: 2 moles 1. Presión: 1,013 x 105 Pa (1 atm)
2. Masa: 8,0 g 2. Volumen: 44,8 L
3. Temperatura: 273 K (0°C)

Rpta. D

109


5. Señale la alternativa INCORRECTA
A) Nanómetro (nm) : 10–9 m.
B) Kilokelvin (kK) : 10 3 K.
C) Miliamperio (mA): 10– 3 A.
D) Picomol (pmol): 10– 12 mol.
E) Teragramo (Tg) : 1012 kg.

Solución:

A) Nano (n) : 10–9
B) Kilo (k) : 10 3
C) Mili (m): 10– 3
D) Pico (p): 10– 12
E) Tera (T) : 1012
Las equivalencias son correctas, sin embargo para el caso de la masa la unidad
base de conversión es el gramo y no el kilogramo.
Rpta. E

6. Se sabe que la temperatura en la superficie del sol es aproximadamente seis mil
grados Celsius. Exprese dicha temperatura en grados Fahrenheit.
5 4 3
A) 1,10 x 10 B) 1,08 x 10 C) 1,10 x 10
5 4
D) 1,08 x 10 E) 1,50 x 10

Solución:
o o o
C F - 32 6 000 F - 32
= ⇒ = ⇒ o F = 10 832 = 1,08 x 10 4 °F
100 180 100 180
Rpta. B

7. En Inglaterra, en el exterior de una casa, una corriente de aire frío hace bajar la
temperatura registrada en un termómetro de 81°F hasta 54°F. ¿Cual es el cambio
de temperatura expresada en R y °C?

A) 27 y 15 B) 28 y 16 C) 15 y 27 D) 10 y 12 E) 27 y 10

Solución:

ΔT= Tf – Ti = 54°F – 81°F = –27°F (el signo negativo indica disminucion o descen-
so de temperatura)

ΔT ⇒ 100°C = 100K = 180 °F = 180 R
ΔT ⇒ 1°C = 1K = 1,8 °F = 1,8 R
ΔT ⇒ 1,8°F = 1,8 R ⇒ ΔT = 27 R

ΔT ⇒ 1,8°F ---------- 1°C
27°F --------- X °C = 15°C ⇒ ΔT = 15 °C
Rpta. A
110


8. Marque la secuencia correcta de verdadero (V) o falso (F) respecto a las respectivas
equivalencias.

I. Masa del electrón: 9,11 x 10–31 kg = 9,11 x 10–28 g
o
II. Radio atómico del Rubidio: 2,5 A = 250 nm
II. Presión sanguínea: 10 kPa = 75 mm Hg
o
Datos : 1 A = 10–10 m 760 mm Hg = 1,013 x 105 Pa

A) FFF B) FVV C) VVV D) VVF E) VFV

Solución:

⎛ 10 3 g ⎞
I. VERDADERO : 9,11x10 −31kg ⎜ ⎟ = 9,11 x 10 -28 g
⎜ 1kg ⎟
⎝ ⎠
O ⎛ 10 −10 m ⎞ ⎛ 1nm ⎞
II. FALSO: 2,5 A ⎜ ⎟⎜ ⎟ = 0,25 nm
⎜ O ⎟ ⎜ −9 ⎟
⎝ 1A ⎠ ⎝ 10 m ⎠

⎛ 10 3 Pa ⎞ ⎛ 760mmHg ⎞ 7,6 x 10 6
⎜
III. VERDADERO: 10kPa ⎜ ⎟⎜
⎟ ⎟= mm Hg = 75 mm Hg
5 5
⎝ 1kPa ⎠ ⎝ 1,013x10 Pa ⎠ 1,013x10
Rpta. E

9. La velocidad de la luz en el vacío es 1,08 x 109 km / h. Exprese esta velocidad en
unidades SI.
5 8 10
A) 3,6 x 10 B) 1,0 x 10 C) 3,0 x 10
8 9
D) 3,0 x 10 E) 1,8 x 10

Solución:

km ⎛ 1h ⎞ ⎛ 10 3 m ⎞ 9 m 8 m
1,08 x 10 9 ⎜ ⎜ ⎟
⎜ 3,6 x 10 3 s ⎟ ⎜ 1 km ⎟ = 0,3 x 10 s = 3,0 x 10 s
h ⎝ ⎟
⎠⎝ ⎠

Rpta. D

10. Un diamante de 350 kilates tiene 0,5 dm de largo, 4 cm de ancho y 10 mm de espe-
sor. Determine la densidad de la gema en g / cm3.
Dato: 1 kilate = 0,2 g

A) 3,2 B) 1,8 C) 3,5 D) 3,6 E) 2,5

111


Solución:

Masa del diamante:
⎛ 0,2 g ⎞
350 Kilates ⎜ ⎟ = 70 g
⎝ 1 kilate ⎠
Volumen del diamante:
⎛ 10 -1 m ⎞ ⎛ 1 cm ⎞
0,5 dm ⎜⎜ ⎟ ⎜
⎟ ⎜ -2 ⎟ = 5 cm
⎟
⎝ 1 dm ⎠ ⎝ 10 m ⎠
⎛ 10 -3 m ⎞ ⎛ 1 cm ⎞
10 mm ⎜ ⎟ ⎜ -2 ⎟ = 1 cm
⎜ ⎟
⎜ 1 mm ⎟ ⎝ 10 m ⎠
⎝ ⎠
VDIAMANTE = 5 cm x 4 cm x 1cm = 20 cm3 = 20 mL
DDIAMANTE = Masa / Volumen = 70 g/ 20 mL = 3,5 g / cm3
Rpta. C

REFORZAMIENTO PARA LA CASA

1. Indique la correspondencia Magnitud – Símbolo Unidad SI
a) Intensidad luminosa ( ) J
b) Densidad ( ) cd
c) Energía ( ) kg
d) Masa ( ) kgm–3
A) a, b, d, c B) b, d, a, c C) c, a, d, b D) d, b, c, a E) c, a, b, d
Solución:

a) Intensidad luminosa (c ) J
b) Densidad ( a ) cd
c) Energía ( d ) kg
d) Masa ( b) kgm–3
Rpta. C

2. Complete el siguiente enunciado con las unidades adecuadas.
“El radio atómico de un átomo se puede medir en…………….., mientras que la dis-
tancia de la tierra a la luna se puede medir en……………………………………”

A) picómetros (10–9 m) – decimetros (10–1 m)
B) terámetros (1012 m) – centimetros (10–2 m)
C) metros (100 m) – kilómetros (103 m)
–9
D) nanómetros (10 m) – exametros (1018 m)
E) terámetros (1012 m) – micrómetros (10–6 m)

112


Solución:

El radio del átomo es muy pequeño, por lo que se puede medir con un submúltiplo
de la unidad como el nanómetro (10–9 m), mientras que la distancia de la tierra a la
luna es muy grande por lo que se puede medir con un múltiplo como el exámetro
(1018 m).
Rpta. D
3. Ordene en forma ascendente de tamaño, a cuatro esferas de distintos metales cu-
yas masas son iguales.
Datos: ρ ρAl = 2,7g/mL ρCu = 8,9 g/mL ρPb = 11,4 g/mL
Fe = 7,5 g/mL

A) Al, Fe, Cu y Pb B) Pb, Fe, Cu y Al C) Al, Cu, Fe y Pb
D) Pb, Cu, Fe y Al E) Pb, Al, Cu y Fe
Solución:

Densidad = Masa/ Volumen. Si las 4 esferas tienen la misma masa, El menor vo-
lumen corresponde a la esfera del metal de mayor densidad y el mayor volumen co-
rresponde al metal de menor densidad. ⇒ Pb, Cu, Fe y Al.
Rpta. D

4. Indique las conversiones correctas.
I. Dos toneladas métricas de Au: 2x104 kg = 2,0 x 106g
II. Energía para disociar 1 molécula H2: 7,2 x 10–19 J = 7,2 x 10–19 kgm2s–2
III. Densidad del H2O: 1,0 g/ mL = 1,0 x 10–3 kg/L
IV. Calor específico del agua: 1,0 cal/g°C = 1,53 x 101 Unidades SI

Datos : 1caloria = 4,184 J 1 TM = 103 kg
A) l y II B) II y III C) I y IV D) II y IV E) II, III y IV
Solución:

I. INCORRECTO: Dos toneladas métricas de Au : 2x103 kg = 2,0 x 106g

II. CORRECTO: Energía para disociar 1 molécula de H2:
7,2 x 10–19 J = 7,2 x 10–19 kgm2s–2 ⇒ 1 J = 1 kg. m2.s–2

III. INCORRECTO: Densidad del H2O: 1,0 g/ mL = 1,0 kg/L

g ⎛ 1kg ⎞ ⎛ 10 3 mL ⎞ kg
1,0 ⎜ 3 ⎟⎜
⎜ 10 g ⎟ ⎜ 1L ⎟ = 1,0 L
⎟
mL ⎝ ⎠⎝ ⎠

IV. CORRECTO Calor específico del agua expresado en unidades SI:

113


cal ⎛ 4,184J ⎞ ⎛ 10 3 g ⎞ ⎛ 1o C ⎞ J
⎟⎜⎜ 1kg ⎟ ⎜ 274K ⎟ = 1,53x10 kgK
1
1 ⎜ ⎟⎜ ⎟
g°C ⎝ 1cal ⎠ ⎝ ⎠⎝ ⎠
Rpta. D

5. Una botella de acido sulfúrico contiene 2 lb de acido. ¿Que cantidad de acido nítrico,
en unidad básica SI, puede almacenarse en la misma botella?
Datos: ρH S O 1 , 6 g / m L ρH N O 1 , 4 g / m L 1lb = 454 g
2 4 = 3 =

A) 5,68 x 10–1 B) 7,95 x 101 C) 7,95 x 102 D) 5,68 x 10–4 E) 7,95 x 10–1

Solución:

H2SO4
⎛ 454g ⎞ ⎛ 1mL ⎞
V = 2 lb x ⎜
⎜ ⎟
⎟ ⎜
⎜ 1,6 g ⎟ = 567,5 mL
⎟
⎝ 1 lb ⎠ ⎝ ⎠

HNO3

m g
ρ= → m = ρ x V = 1,4 x 567,5 mL = 794,5 g = 0,7945 kg = 7,95 x 10 -1 kg
V mL

Rpta. E

114


QUÍMICA
“Hay dos razones de peso por las que es preciso
que la sociedad apoye la ciencia básica. Una es
pragmatica : la oscura química sintética de ayer
hoy cura enfermedades; la física teórica de ayer es
la defensa nuclear de hoy. La otra razón es cul-
tural. La esencia de nuestra civilización consiste
en explorar y analizar la naturaleza del hombre y
lo que lo rodea”.

LA QUÍMICA ESTA EN TODAS PARTES
♦ Ya sea que se analicen sustancias en el suelo, en el agua o en el aire
– la QUÍMICA está presente.

♦ Si se desarrollan equipos ligeros para materiales deportivos o nue-
vos materiales semiconductores – la QUÍMICA está presente.

♦ Cuando se trabaja en el desarrollo de nuevos aerosoles que no des-
truyan la capa de ozono o de nuevas sustancias para combatir el si-
da, el cáncer, u otros misterios de la medicina – la QUÍMICA está
presente.

LOS FUNDAMENTOS DE LA QUÍMICA, OCUPAN UN LUGAR EN EL
CENTRO DE TODA CIENCIA, POR LO TANTO LA QUÍMICA ESTÁ
EN TODAS PARTES.

Los profesores del curso esperamos en verdad, que disfrutes tu aven-
tura en el mundo de la QUIMICA. ¡El éxito depende de ti!, recuerda
que el ascenso hacia nuevas alturas puede ser difícil, pero el “paisa-
je que se ve desde las alturas” es fantástico.

115


La Química es la ciencia que estudia la materia, sus propiedades físicas y químicas, los
cambios y transformaciones que experimenta y las variaciones de energía que acompa-
ñan a dicha transformación.

El avance de la química como ciencia sigue el siguiente método científico

PROBLEMA

OBSERVACIÓN

HIPÓTESIS NUEVA
HIPÓTE-

EXPERIMENTACIÓN

TEORÍA

LEY

MAGNITUD: todo aquello que se puede medir y cuantificar

c) Magnitudes básicas. Ejm. La masa
d) Magnitudes derivadas. Ejm. El volumen.

MAGNITUDES Y UNIDADES DEL SISTEMA INTERNACIONAL (SI)

MAGNITUDES Y UNIDADES BÁSICAS MAGNITUDES Y UNIDADES
DERIVADAS
MAGNITUD UNIDAD SÍMBOLO MAGNITUD SÍMBOLO
Masa kilogramo kg Volumen m3
Longitud metro M Densidad kg/m3
Temperatura kelvin K Velocidad m/s
Tiempo segundo s Fuerza kg.m/s2 = 1 N
Intensidad amperio A Área m2
de corriente
Intensidad candela cd Presión N/m2 = 1 Pa
luminosa
Cantidad de mol mol Aceleración m/s2
sustancia

116


Múltiplos
Deca(da) Kilo Mega(M) Giga(G) Tera Peta
(k) (T) (P)
101 103 106 109 1012 1015
Unidad
Base (100)

Submúltiplos
Deci(d) Centi (c) Mili (m) Micro Nano Pico
(μ) (n) (p)
10–1 10–2 10–3 10–6 10–9 10–12

Ejemplo : (submúltiplo) 1 mm = 10–3 m (Múltiplo) 1 Mm = 106 m

NOTACIÓN CIENTÍFICA: 120 000 = 1,2 x 105 y 0,000012 = 1,2 x 10–5

FACTOR DE CONVERSIÓN: Se generan a partir de una igualdad

1 pulgada = 2, 54 cm

1pu lg . 2,54 cm
254 cm x = 100 pulg. 10 pulg. x = 25,4 cm
2,54 cm 1 pu lg .

DENSIDAD : Relación de la masa con el volumen
masa (g) masa (g)
D= o
Volumen (mL o cm 3 ) Volumen (L )
para sólidos o líquidos para gases

VALORES DE LA DENSIDAD PARA ALGUNAS SUSTANCIAS

Sólidos g/cm3
Oro 19,30
Plomo 11,30
Aluminio 2,70
Hierro 7,86
Cobre 8,92
Sal de mesa 2,16
Líquidos g / mL
Agua pura 0,998
Agua de mar 1,03
Mercurio 13,6
Gases g/L
Aire 1,29
Oxígeno 1,43
Dióxido de carbono 1,96

117


SEMANA Nº 1 MAGNITUDES, UNIDADES, CONVERSIONES Y DENSIDAD

1. Complete el siguiente cuadro con Magnitudes y Unidades Básicas del sistema inter-
nacional (S.I.).

Magnitud Unidad
Cantidad de
(I)
sustancia
(II) Amperios (A)
(III) Kelvin (K)
Longitud (IV)

A) Kilogramo (kg), Intensidad de corriente, temperatura, kilómetro (km).
B) Mol (mol), carga de corriente eléctrica, temperatura, metro (m).
C) Kilogramo (kg), Intensidad de corriente, Intensidad luminosa, metro (m).
D) Gramo (g), Intensidad de corriente, intensidad luminosa, kilómetro (km).
E) Mol (mol), Intensidad de corriente, temperatura, metro (m).

Solución:

Magnitud Unidad
Cantidad de
mol(mol)
sustancia
Intensidad de
Amperios (A)
corriente
Temperatura Kelvin (K)
Longitud metro (m)
Rpta. E

2. Indique el número de magnitudes básicas y magnitudes derivadas, respectivamente,
en la siguiente descripción:
“Dos moles de gas helio tienen una masa de 8,0 g. A condiciones normales, es decir
1,013 x 105 Pa y 273 K, ocupan un volumen de 44,8 L”

A) 2 y 3 B) 3 y 1 C) 2 y 2 D) 3 y 2 E) 4 y 1

Solución:

Magnitud Básica: Magnitud Derivada:
1. Cantidad de sustancia: 2 moles 1. Presión: 1,013 x 105 Pa (1 atm)
2. Masa: 8,0 g 2. Volumen: 44,8 L
3. Temperatura: 273 K (0°C)

Rpta. D

118


3. Señale la alternativa INCORRECTA
A) Nanómetro (nm) : 10–9 m.
B) Kilokelvin (kK) : 10 3 K.
C) Miliamperio (mA): 10– 3 A.
D) Picomol (pmol): 10– 12 mol.
E) Teragramo (Tg) : 1012 kg.

Solución:

A) Nano (n) : 10–9
B) Kilo (k) : 10 3
C) Mili (m): 10– 3
D) Pico (p): 10– 12
E) Tera (T) : 1012
Las equivalencias son correctas, sin embargo para el caso de la masa la unidad
base de conversión es el gramo y no el kilogramo.
Rpta. E

4. Se sabe que la temperatura en la superficie del sol es aproximadamente seis mil
grados Celsius. Exprese dicha temperatura en grados Fahrenheit.
5 4 3
A) 1,10 x 10 B) 1,08 x 10 C) 1,10 x 10
5 4
D) 1,08 x 10 E) 1,50 x 10

Solución:
o o o
C F - 32 6 000 F - 32
= ⇒ = ⇒ o F = 10 832 = 1,08 x 10 4 °F
100 180 100 180
Rpta. B

5. Un diamante de 350 kilates tiene 0,5 dm de largo, 4 cm de ancho y 10 mm de espe-
sor. Determine la densidad de la gema en g / cm3.
Dato: 1 kilate = 0,2 g

A) 3,2 B) 1,8 C) 3,5 D) 3,6 E) 2,5

Solución:

Masa del diamante:
⎛ 0,2 g ⎞
350 Kilates ⎜ ⎟ = 70 g
⎝ 1 kilate ⎠

Volumen del diamante:
⎛ 10 -1 m ⎞ ⎛ 1 cm ⎞
⎜
0,5 dm ⎜ ⎟ ⎜
⎟ ⎜ -2 ⎟ = 5 cm
⎟
⎝ 1 dm ⎠ ⎝ 10 m ⎠

119


⎛ 10 -3 m ⎞ ⎛ 1 cm ⎞
10 mm ⎜ ⎟ ⎜ -2 ⎟ = 1 cm
⎜ ⎟
⎜ 1 mm ⎟ ⎝ 10 m ⎠
⎝ ⎠
VDIAMANTE = 5 cm x 4 cm x 1cm = 20 cm3 = 20 mL
DDIAMANTE = Masa / Volumen = 70 g/ 20 mL = 3,5 g / cm3
Rpta. C

REFORZAMIENTO PARA LA CASA
1. Marque la secuencia correcta de verdadero (V) o falso (F):

III. Las propiedades del elemento nitrógeno es estudiada por la Química Orgánica.
II. El tiempo de vigencia de un fármaco es estudiado por la Química Inorgánica.
IV. La cantidad de hierro en la sangre es determinada por la Bioquímica.
IV. El proceso de respiración de las plantas es estudiada por la Fisicoquímica.

A) FFFF B) FVVF C) VVVF D) VVFV E) VVVV

Solución:

I. FALSO: Las propiedades del elemento nitrógeno, así como los restantes ele-
mentos químicos es estudiada por la Química Inorgánica.
II. FALSO: El tiempo de vigencia de un fármaco es estudiado por la FISICOQUI-
MICA, específicamente en Cinética Química.

III. FALSO: La cantidad de hierro en la sangre, o cualquier elemento en cualquier
tipo de materia es determinada por Química Analítica

IV. FALSO: Los procesos químicos que involucran a los seres vivos es estudiado
por la BIOQUIMICA.
Rpta. A

2. Indique la correspondencia Magnitud – Símbolo unidad SI

a) Intensidad luminosa ( ) J
b) Densidad ( ) cd
c) Energía ( ) kg
d) Masa ( ) kg m–3

A) a, b, d, c B) b, d, a, c C) c, a, d, b D) d, b, c, a E) c, a, b, d

Solución:

a) Intensidad luminosa ( c) J
b) Densidad ( a) cd
c) Energía ( d) kg
d) Masa ( b) kgm–3
Rpta. C

120


3. Marque la secuencia correcta de verdadero (V) o falso (F) respecto a las respectivas
equivalencias.
I. Masa del electrón: 9,11 x 10–31 kg = 9,11 x 10–28 g
o
II. Radio atómico del Rubidio: 2,5 A = 250 nm
II. Presión sanguínea: 10 kPa = 75 mm Hg
o
Datos : 1 A = 10–10 m 760 mm Hg = 1,013 x 105 Pa

A) FFF B) FVV C) VVV D) VVF E) VFV

Solución:

⎛ 10 3 g ⎞
I. VERDADERO: 9,11x10 −31kg ⎜ ⎟ = 9,11 x 10 -28 g
⎜ 1kg ⎟
⎝ ⎠
O ⎛ 10 −10 m ⎞ ⎛ 1nm ⎞
II. FALSO: 2,5 A ⎜ ⎟⎜ ⎟ = 0,25 nm
⎜ O ⎟ ⎜ 10 −9 m ⎟
⎝ ⎠
⎝ 1A ⎠

⎛ 10 3 Pa ⎞ ⎛ 760mmHg ⎞ 7,6 x 10 6
⎜
III. VERDADERO: 10kPa ⎜ ⎟⎜
⎟ ⎟= mm Hg = 75 mm Hg
5 5
⎝ 1kPa ⎠ ⎝ 1,013x10 Pa ⎠ 1,013x10
Rpta. E

4. La velocidad de la luz en el vacío es 1,08 x 109 km / h. Exprese esta velocidad en
unidades SI.
5 8 10
A) 3,6 x 10 B) 1,0 x 10 C) 3,0 x 10
8 9
D) 3,0 x 10 E) 1,8 x 10
Solución:

km ⎛ 1h ⎞ ⎛ 10 3 m ⎞ 9 m 8 m
1,08 x 10 9 ⎜ ⎜ ⎟
⎜ 3,6 x 10 3 s ⎟ ⎜ 1 km ⎟ = 0,3 x 10 s = 3,0 x 10 s
h ⎝ ⎟
⎠⎝ ⎠

Rpta. D

5. Una botella de acido sulfúrico contiene 2 lb de acido. ¿Que cantidad de acido nítrico,
en unidad básica SI, puede almacenarse en la misma botella?
Datos: ρ H 2 S O 4 1 , 6 g / m L ρH N O 1 , 4 g / m L 1lb = 454 g
= 3 =

A) 5,68 x 10–1 B) 7,95 x 101 C) 7,95 x 102 D) 5,68 x 10–4 E) 7,95 x 10–1

121


Solución:

H2SO4
⎛ 454g ⎞ ⎛ 1mL ⎞
⎜
V = 2 lb x ⎜ ⎟
⎟ ⎜
⎜ 1,6 g ⎟ = 567,5 mL
⎟
⎝ 1 lb ⎠ ⎝ ⎠

HNO3

m g
ρ= → m = ρ x V = 1,4 x 567,5 mL = 794,5 g = 0,7945 kg = 7,95 x 10 -1 kg
V mL

Rpta. E

122

Solsem01

Más contenido relacionado

Similar a Solsem01

Solsem01