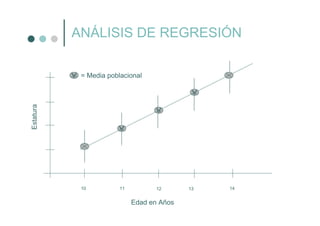
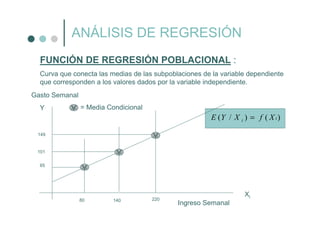
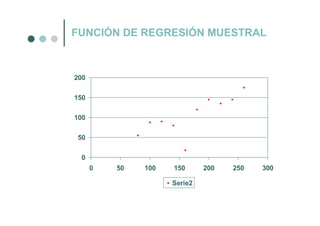
El documento trata sobre el análisis de regresión, que estudia la dependencia de una variable respecto a una o más variables explicativas con el objetivo de explorar o cuantificar la media de la variable dependiente en base a los valores de las variables independientes. Examina conceptos como la función de regresión poblacional, la función de regresión muestral, y el objetivo de estimar la función de regresión poblacional a partir de la función de regresión muestral.

1. ANÁLISIS DE REGRESIÓN

2. ANÁLISIS DE REGRESIÓN
En términos generales, el análisis de Regresión trata sobre
el estudio de la dependencia de un fenómeno económico
respecto de una o varias variables explicativas, con el
objetivo de explorar o cuantificar la media o valor promedio
poblacional de la primera a partir de un conjunto de valores
conocidos o fijos de la/s segunda/s.

3. ANÁLISIS DE REGRESIÓN
10 11 12 13 14
V
V
V
Edad en Años
Estatura
V = Media poblacional

4. ANÁLISIS DE REGRESIÓN
Estudiar y predecir el valor
promedio de una variable
sobre la base de valores
fijos de otras variables.
Existe una asimetría en el
tratamiento que se les da a
las variables.
La variable dependiente es
aleatoria o estocástica: su
valor depende de una
distribución de probabilidades.
Las variables independientes
tienes valores fijos en
muestras repetidas.
El objetivo es medir el
grado de asociación
lineal entre dos
variables.
El tratamiento de las
variables es simétrico:
No se distinguen entre
variable dependiente y
variable explicativa.
Se asume que las dos
variables son simétricas.
REGRESIÓN CORRELACIÓN

5. ANÁLISIS DE REGRESIÓN
La forma más intuitiva de formarse una primera
impresión sobre el tipo de relación que existe entre dos
variables es a través del Diagrama de Dispersión.
Un diagrama de dispersión es un gráfico en el que una de las variables (Xi)
se coloca en el eje de las abscisas y la otra (Yi) en el eje de las ordenadas y
los pares de puntuaciones de cada sujeto (xi,yi) se representan como una
nube de puntos.

6. ANÁLISIS DE REGRESIÓN
0
5
10
15
20
25
0 5 10 15 20 25
Variable X
VariableY
CORRELACIÓN POSITIVA
0
5
10
15
20
25
-25 -20 -15 -10 -5 0
Variable X
VariableY
CORRELACIÓN NEGATIVA
0
100
200
300
400
500
0 5 10 15 20 25
Variable X
VariableY
CORRELACIÓN NO LINEAL
0
5
10
15
20
25
30
0 20 40 60 80
Variable X
VariableY
AUSENCIA DE CORRELACIÓN

7. 173161149137125113101897765
Medias
Condiciona
les
12119661043685750678707445462325TOTAL
191162115
18518916014012511388
180175157145135118108988575
178165152144130116103948070
17515514014012011095907465
15214513713611510793847060
15013713512011010280796555Gasto de
Consumo
Familiar
Semanal
26024022020018016014012010080
INGRESO FAMIILIAR
ANÁLISIS DE REGRESIÓN

8. ANÁLISIS DE REGRESIÓN
40
80
120
160
200
50 75 100 125 150 175 200 225 250 275
Ingreso Semanal
GastodelConsumoFinal

9. FUNCIÓN DE REGRESIÓN POBLACIONAL :
Curva que conecta las medias de las subpoblaciones de la variable dependiente
que corresponden a los valores dados por la variable independiente.
ANÁLISIS DE REGRESIÓN
V = Media Condicional
V
V
V
Xi
Y
80 140 220
65
101
149
Ingreso Semanal
Gasto Semanal
)()/( ii XfXYE =

10. ANÁLISIS DE REGRESIÓN
Población (Universo): un conjunto total de
elementos que poseen una o más características
en común.
Hace referencia al conjunto total de elementos
que se desea estudiar.
Pueden ser finitas, formadas por un número
finitos de elementos, o infinitas donde el
número de elementos es infinitos.
Dado que es imposible describir con exactitud todas las características
de una población infinita o conformada por un gran número de
elementos, lo habitual es trabajar con muestras.

11. ANÁLISIS DE REGRESIÓN
Muestra Es un subconjunto de la población.
Suelen ser conjuntos de elementos de
tamaño reducido.
La información que contiene permite extraer
conclusiones sobre las propiedades de la
población, siempre que los elementos que
conformen la muestra sean representativos
de la población.

12. ANÁLISIS DE REGRESIÓN
FUNCIÓN DE REGRESIÓN MUESTRAL :
Son aproximaciones de la función de regresión poblacional. Las diferencias
con respecto a esta última son ocasionadas por las fluctuaciones
muestrales. Por lo que se tendrían N FRMs para N muestras diferentes y
tales FRMs no necesariamente coinciden.
OBJETIVO PRINCIPAL :
Del análisis de regresión es por tanto estimar la función de regresión
poblacional (FRP) a partir de la función de regresión muestral (FRM).

13. FUNCIÓN DE REGRESIÓN MUESTRAL
0
50
100
150
200
0 50 100 150 200 250 300
Serie1

14. FUNCIÓN DE REGRESIÓN MUESTRAL
0
50
100
150
200
0 50 100 150 200 250 300
Serie2

15. FUNCIÓN DE REGRESIÓN MUESTRAL
0
50
100
150
200
80 100 120 140 160 180 200 220 240 260
FRM1 FRM2

16. ANÁLISIS DE REGRESIÓN
FUNCIÓN DE REGRESIÓN MUESTRAL :
ii uXYi ˆˆˆ
21 ++= ββ
FUNCIÓN DE REGRESIÓN POBLACIONAL :
ii uXYi ++= 21 ββ