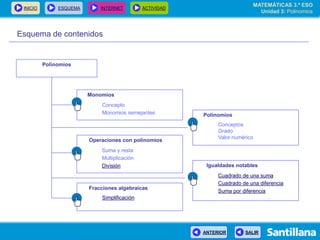
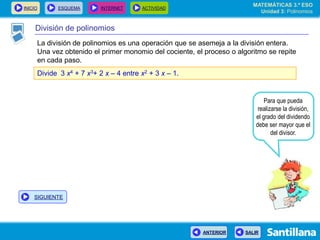
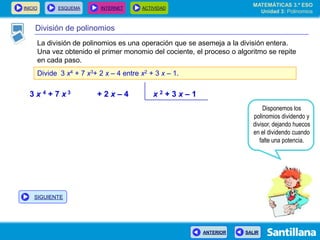
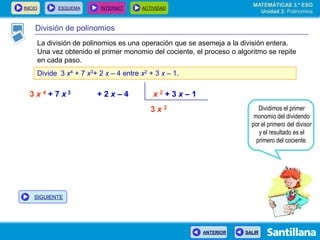
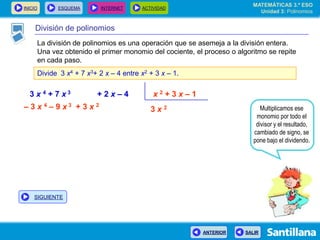
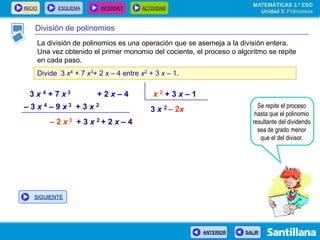
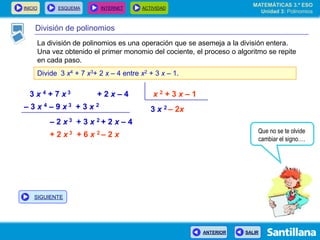
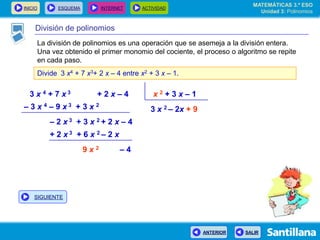
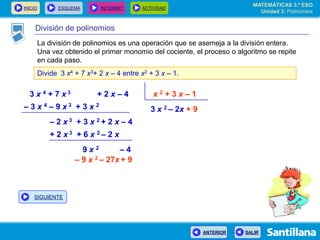
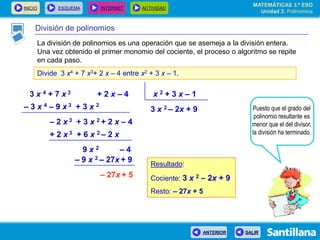
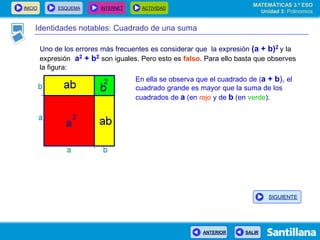
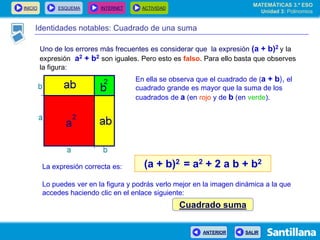
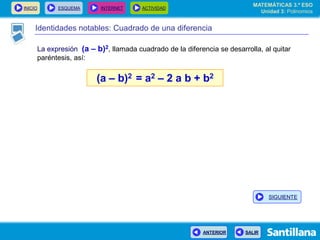
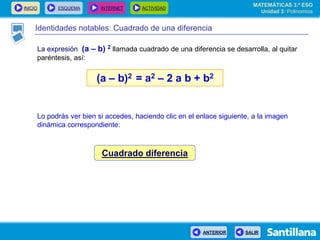
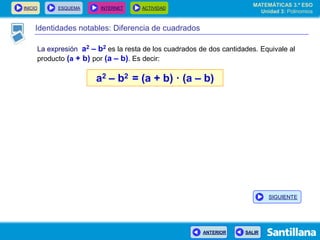
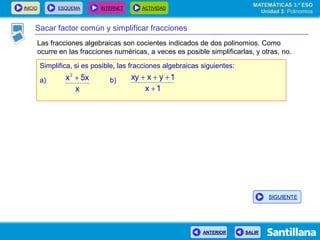
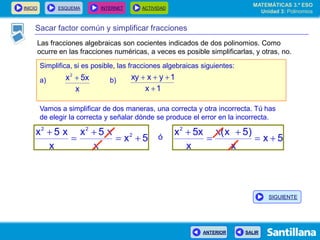
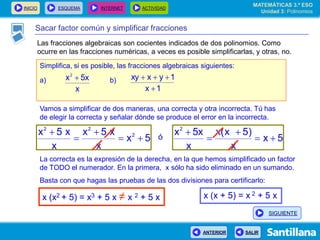
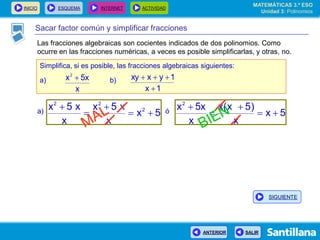
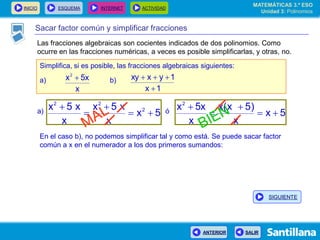
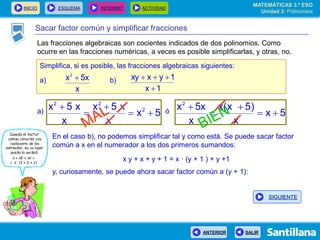
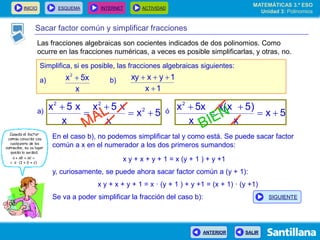
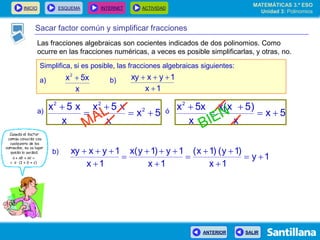
El documento presenta información sobre polinomios. Explica que los polinomios son la base del álgebra, la cual surgió en el siglo IX en Bagdad. Incluye un esquema con los conceptos clave sobre polinomios como monomios, grado, operaciones y fracciones algebraicas. Finalmente, muestra ejemplos de división de polinomios y de identidades notables.