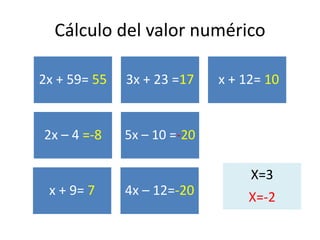
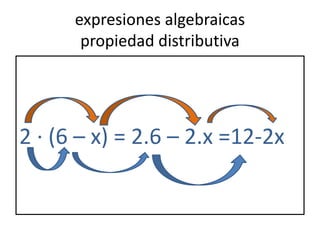
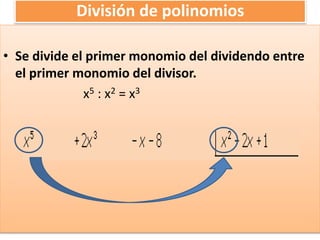
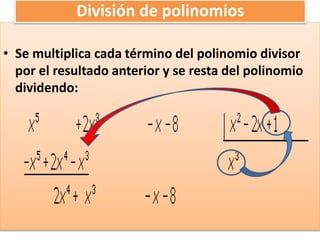
Este documento trata sobre los fundamentos básicos de los polinomios. Explica qué son las expresiones algebraicas y los diferentes tipos como monomios, binomios, trinomios y polinomios. También describe las partes de un monomio como el coeficiente, la parte literal y el grado. Finalmente, cubre operaciones básicas con polinomios como suma, resta, multiplicación y factorización.

1. POLINOMIOS
FUNDAMENTOS BÁSICOS
3º ESO

2. Expresiones algebraicas
Una expresión algebraica es una combinación
de letras y números ligadas por los signos de la
operaciones:adición, sustracción,multiplicación,
división y potenciación.
• Longitud de la circunferencia:
L = 2∏r, r es el radio de la circunferencia.
• Área del cuadrado:
S = l2, l es el lado del cuadrado.

3. Valor numérico de una expresión algebraica
El valor numérico de una expresión algebraica,
para un determinado valor, es el número que
se obtiene al sustituir las indeterminadas por
valores concretos
L(r) = 2∏r,
r = 5 cm. L (5)= 2 · ∏ . 5 = 31,41 cm

4. Tipos de expresiones algebraicas
• Un MONOMIO es una expresión algebraica formada
por un solo término. 5 x2
• Un BINOMIO es una expresión algebraica formada
por dos términos. 6 x7 - 2
• Un TRINOMIO es una expresión algebraica formada
por tres términos. 3 x5 + 4 x3 - x2
• Un POLINOMIO es una expresión algebraica
formada por más de un término. 5 x6 + 3 x4 - x2+ 3 x

5. Polinomios
• Un polinomio es una suma de términos
llamados monomios no semejantes:
P(x)= 5 x6 + 3 x4 - x2+ 3 x+4
Por ello es importante saber más cosas sobre los
monomios

6. MONOMIO
• Un monomio es una expresión algebraica en
la que las únicas operaciones que aparecen
entre las variables son el producto y la
potencia de exponente natural.
2x2 y3 z

7. – 4 a3b
TÉRMINO
PARTE LITERAL
PARTE NUMÉRICA
COEFICIENTE
GRADO 3+1
Partes de un monomio

8. Partes de un monomio
• El coeficiente del monomio es el número que
aparece multiplicando a las variables. – 4 a3b
• La parte literal está constituida por las letras y sus
exponentes. – 4 a3b
• El grado de un monomio es la suma de todos los
exponentes de las letras o variables. – 4 a3b1
El grado es: 3 + 1 = 4

9. GRADO DE UN MONOMIO
• El grado de un monomio es la
suma de todos los exponentes de
las letras o variables.
El grado de:
2x2 y3 z
es: 2 + 3 + 1 = 6

10. GRADO DE UN POLINOMIO
• El grado de un polinomio es el
mayor grado de los términos que
la forman:
El grado de:
P(x)= x4 + x3 − 2x2+ 3x + 2
es: 4

11. Monomios semejantes
• Dos monomios son semejantes cuando tienen
la misma parte literal.
2x2 y3 z es semejante a 5x2 y3 z

12. Cálculo del valor numérico
2x + 59= 3x + 23 = x + 12=
2x – 4 = 5x – 10 =
X=3
X=-2
x + 9= 4x – 12=

13. Cálculo del valor numérico
2x + 59= 65 3x + 23 =32 x + 12= 15
2x – 4 = 2 5x – 10 = 5
X=3
X=-2
x + 9=12 4x – 12=0

14. Cálculo del valor numérico
2x + 59= 55 3x + 23 =17 x + 12= 10
2x – 4 =-8 5x – 10 =-20
X=3
X=-2x + 9= 7 4x – 12=-20

15. Recordamos
cosas de 1º de
ESO

16. ¿cómo se hacen las sumas y las restas
algebraicas?
• Sumo o resto sólo el coeficiente.
• 3 ₧ + 5 € + 7₤- 2 ₧ + 4 € + 9₤=
• 3 ₧ - 2 ₧ =
• 5 € + 4 € =
• 7₤+ 9₤=

17. ¿cómo se hacen las sumas y las restas
algebraicas?
• Sumo o resto sólo el coeficiente.
• 3 ₧ + 5 € + 7₤- 2 ₧ + 4 € + 9₤=
= 1 ₧ + 9 € + 16 ₤
• 3 ₧ - 2 ₧ = 1 ₧
• 5 € + 4 € =9 €
• 7₤+ 9₤=16 ₤

18. Suma y resta de expresiones
algebraicas
• a)5x + 2 - x + 10=
• b) 1 + 3x + 2x – 7=
• c) 2 + 7x - 4 – 3x=
• d) x – 18 + 2x – 3=
• e) – 5 – 2x + 3 – 8x – 2=

19. Suma y resta de expresiones
algebraicas
• a)5x + 2 - x + 10= 4x+12
• b) 1 + 3x + 2x - 7= 5x-6
• c) 2 + 7x - 4 – 3x= 4x - 2
• d) x – 18 + 2x – 3= 3x - 21
• e) – 5 – 2x + 3 – 8x – 2= - 10x- 2

20. Multiplicar y dividir expresiones
algebraicas
• Se opera:
• la parte NUMÉRICA con la parte
NUMÉRICA
• la parte LITERAL con la parte
LITERAL

21. Multiplicar expresiones algebraicas
• a) 3x . 2 = 3.2.x = 6 x
• b) 5x . x = 5 x2
• c) 2x . 4x = 2.4.x.x = 8 x2

22. Multiplicar expresiones algebraicas
• Cuando se multiplican potencias de
la misma base, se suman los
exponentes (aplica a la parte literal)
8 x2 . 2 x3 = 8.2 x2. x3 = 16 x2+3 = 16 x5

23. Multiplicar expresiones algebraicas
• ejemplos
a. 8 . 5 x6 =
b. 6x.2 y=
c. 3x.-10 . 2x=
d. 2x. 5xy2. 3x=

24. Multiplicar expresiones algebraicas
• ejemplos
a. 8 . 5 x6 = 40 x6
b. 6x.2 y= 12 x y
c. 3x.-10 . 2x= -60 x2
d. 2x. 5xy2. 3x= 30 x3 y2

25. expresiones algebraicas
propiedad distributiva
2 · (6 – x) = 2.6 – 2.x =12-2x

26. Multiplicar estas expresiones algebraicas
a) 5(2 – x)
b) 3(x + 6) =
c) 4(6 + 2x) =
d) 3 (x + 8) =
e) – 5(x – 5) =
f) 2(x + 6) =
g) 10(x – 2) =

27. Multiplicar estas expresiones algebraicas
a) 5(2 – x)= 10 – 5x
b) 3(x + 6) =3x + 18
c) 4(6 + 2x) = 24 + 8x
d) 3 (x + 8) = 3x + 24
e) – 5(x – 5) = -5x + 25
f) 2(x + 6) = 2x + 12
g) 10(x – 2) = 10x-20

28. Sacar factor común
El FACTOR COMÚN es el
elemento que
multiplica a TODOS los
términos.

29. Sacar factor común
¿cuál es el FACTOR COMÚN?
• 3+ 9- 12- 21 = 3.(1+3-4-7)
• 120 + 10 -15=5.(24+ 2 -3)
• 2x2 + 4x +10xy= 2x(x+2+5y)
• 6xzy - xz + xy = x(6zy-z+y)
• 4@Ω - 2@ +5 Ω = ninguno

30. Sacar factor común
¿cuál es el FACTOR COMÚN?
• 3+ 9- 12- 21 = 3.(1+3-4-7)
• 120 + 10 -15=5.(24+ 2 -3)
• 2x2 + 4x +10xy= 2x(x+2+5y)
• 6xzy - xz + xy = x(6zy-z+y)
• 4@Ω - 2@ +5 Ω = ninguno

31. Polinomio completo
Polinomio completo
• Es aquel polinomio que tiene todos los
términos desde el término independiente
hasta el término de mayor grado.
P(x) = 2x3 + 3x2 + 5x - 3

32. Ordenar polinomios
• Un polinomio está ordenado si los monomios
que lo forman están escritos de mayor a
menor grado.
P(x) = 2x3 + 5x - 3

33. Reducción de términos semejantes de
un polinomio
Polinomios semejantes
• Dos polinomios son semejantes si verifican
que tienen la misma parte literal.
P(x) = 2x3 + 5x − 3
Q(x) = 5x3 − 2x − 7

34. Suma de polinomios
se suman los coeficientes de los términos del
mismo grado.
P(x) = 2x3 + 5x − 3 Q(x) = 4x − 3x2 + 2x3
1. Ordenamos los polinomios, si no lo están.
Q(x) = 2x3 − 3x2 + 4x
P(x) + Q(x) = (2x3 + 5x − 3) + (2x3 − 3x2 + 4x)
2. Agrupamos los monomios del mismo grado.
P(x) + Q(x) = 2x3 + 2x3 − 3 x2 + 5x + 4x − 3
3. Sumamos los monomios semejantes
P(x) + Q(x) = 4x3- 3x2 + 9x - 3

35. Suma de polinomios
• También podemos sumar polinomios
escribiendo uno debajo del otro, de forma que
los monomios semejantes queden en columnas
y se puedan sumar.
P(x) = 7x4 + 4x2 + 7x + 2 Q(x) = 6x3 + 8x +3
7x4 + 4x2 + 7x + 2
+ 6x3 + 8x +3
7x4 + 6x3 + 4x2 + 15x + 5
P(x) + Q(x) = 7x4 + 6x3 + 4x2 + 15x + 5

36. Resta de polinomios
consiste en sumar el opuesto del sustraendo.
P(x) = (2x3 + 5x − 3) Q(x) =(2x3 − 3x2 + 4x)
P(x) − Q(x) = (2x3 + 5x − 3) − (2x3 − 3x2 + 4x)
P(x) − Q(x) = 2x3 + 5x − 3 − 2x3 + 3x2 − 4x
Se agrupan los términos semejantes
P(x) − Q(x) = 2x3 − 2x3 + 3x2 + 5x − 4x − 3
operando:
P(x) − Q(x) = 3x2 + x − 3

37. Resta de polinomios
• También podemos restar polinomios escribiendo
uno debajo del otro, de forma que los
monomios semejantes queden en columnas y se
puedan sumar después de cambiarle el signo
P(x) = 2x3 + 5x − 3 Q(x) =2x3 − 3x2 + 4x
2x3 + 5x − 3
+ − 2x3 + 3x2 − 4x
3x2 + x − 3
P(x) + Q(x) = 3x2 + x − 3

38. Multiplicación de polinomios
Multiplicación de un número por un polinomio
• Se multiplica el número por los coeficientes del
polinomio
3 · (2x3 − 3 x2 + 4x − 2) = 6x3 − 9x2 + 12x − 6

39. Multiplicación de polinomios
Multiplicación de un monomio por un
polinomio
• Se multiplica la parte numérica por los
coeficientes del polinomio y la parte literal del
monomio por la parte literal del polinomio
3 x2 · (2x3 − 3 x2 + 4x − 2) = 6x5 − 9x4 + 12x3− 6 x2

40. Multiplicación de polinomios
Multiplicación de polinomios
P(x) = 2x2 − 3 Q(x) = 2x3 − 3x2 + 4x
• Se multiplica cada monomio del primer
polinomio por todos los elementos segundo
polinomio.
P(x) · Q(x) = (2x2 − 3) · (2x3 − 3x2 + 4x) =
= 4x5 − 6x4 + 8x3 − 6x3 + 9x2 − 12x =
• Se suman los monomios del mismo grado.
P(x) · Q(x) = 4x5 − 6x4 + 2x3 + 9x2 − 12x

41. Multiplicación de polinomios
Multiplicación de polinomios
P(x) = 2x2 − 3 Q(x) = 2x3 − 3x2 + 4x
• Haciendo la operación en vertical
2x4 − 3x2 + 4x
2x2 − 3
-6x4 + 9x2 - 12x
2x4 − 3x2 + 4x
4x6 -4x4 + 8x3
4x6 − 2x4 + 8x3 -3x2 +4x
P(x) · Q(x) = 4x6 − 2x4 + 8x3 -3x2 +4x

42. Igualdades notables
Se denominan así a algunas operaciones con
polinomios que aparecerán frecuentemente en
los cálculos.
Las más usuales son:
• Cuadrado de un binomio: suma (a + b)2 o
diferencia (a - b)2
• Suma por diferencia: (a + b) · (a - b)

43. Igualdades notables
• Cuadrado de un binomio: suma (a + b)2 o
diferencia (a - b)2
(a + b)2 = (a + b ) · (a + b) = a2 + ab + ba + b2 = a2 +
2ab + b2
De modo similar: (a - b)2 = a2 - 2ab + b2
El cuadrado de un binomio es igual al cuadrado
del primero más o menos dos veces el primero
por el segundo más el cuadrado del segundo

44. Igualdades notables
• Suma por diferencia: (a + b) · (a - b)
• (a + b) · (a - b) = a2 - ab + ba + b2 = a2 - b2
• Siempre recordamos que " suma por diferencia
es igual a la diferencia de los cuadrados

45. División de polinomios
• P(x) = 2x5 + 2x3 − x − 8 Q(x) = 3x2 − 2x + 1
• P(x) : Q(x)
A la izquierda se situa el dividendo. Si el
polinomio no es completo se dejan huecos en
los lugares que correspondan.

46. • Se divide el primer monomio del dividendo entre
el primer monomio del divisor.
x5 : x2 = x3
División de polinomios

47. • Se multiplica cada término del polinomio divisor
por el resultado anterior y se resta del polinomio
dividendo:
División de polinomios

48. Se vuelve a dividir el primer monomio del
dividendo entre el primer monomio del divisor. Y el
resultado lo multiplicamos por el divisor y lo restamos
al dividendo.
2x4 : x2 = 2 x2
División de polinomios

49. División de polinomios
Se procede igual que antes.
5x3 : x2 = 5 x

50. División de polinomios
Se vuelven a hacer las mismas operaciones.
8x2 : x2 = 8
10x − 6 es el resto, porque su grado es menor que el
del divisor y por tanto no se puede continuar dividiendo.