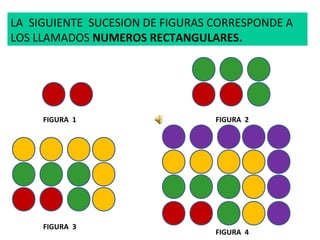
Este documento explica cómo encontrar una expresión algebraica cuadrática para calcular cualquier término en sucesiones numéricas y figurativas mediante el método de diferencias. Se describen diferentes tipos de sucesiones como aritméticas, geométricas y especiales como los números rectangulares. El método de diferencias permite determinar los coeficientes de una expresión cuadrática analizando las diferencias entre los términos.