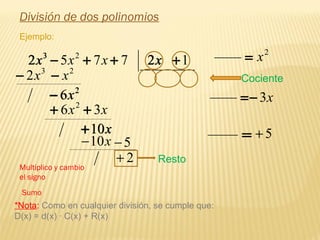
El documento introduce conceptos básicos sobre polinomios como términos, coeficientes, grado y operaciones con polinomios como suma, resta, multiplicación y división. Explica cómo encontrar el valor numérico de un polinomio en un punto determinado, descomponer un polinomio en factores y propiedades de los polinomios como el Teorema del Factor.

2. Introducción. Conceptos básicos.
• Un polinomio es una expresión matemática formada por letras y
números relacionados mediante operaciones aritméticas.
• Un monomio o término es cada uno de los sumandos de un
polinomio.
• La parte literal de un monomio es el conjunto de todas las letras de
dicho monomio.
• El coeficiente de un monomio es el número que multiplica a la
parte literal.
• El grado de un monomio es el número de letras que tiene dicho
término.
• El grado de un polinomio es el mayor de los grados de cada uno
de sus términos.
• Se llama término principal al término de mayor grado.
• Se llama término independiente al término de grado cero.
• Dos términos son semejantes si tienen la misma parte literal.

3. Ejemplo:
( ) 5
3
2
2
4
−+−= x
x
xxP Polinomio de 4 términos
4
2x
P.L.
4
x
Coef. 2
Grado 4
3
2
x
−
P.L.
2
x
Coef. 3
1−
Grado 2
x+
P.L. x
Coef. 1+
Grado 1
5−
P.L. tieneNo
Coef. 5−
Grado 0
El grado del polinomio es 4.
Término independiente  5−
Término principal 
4
2x
Términos semejantes 
4
5
3
3 yx
yyx−
Términos no semejantes 
5
3
2
2
2 xy
yyx−

4. Valor numérico de un polinomio en un punto
Consiste en sustituir la letra/s por el valor que nos den y luego
realizar la operación.
Ejemplo:
( ) 256 36
−=−+−−= xenxxxxP
Halla el valor numérico del siguiente polinomio en el punto indicado.
( )
23
524864
5)2()8(664
5)2()2(6)2(2 36
−=
=−−+−=
=−−+−⋅−−=
=−−+−⋅−−−=−P

5. Suma y resta de polinomios
Sólo se pueden sumar o restar los términos que sean semejantes.
Para restar dos polinomios basta con cambiar los signos del
sustraendo y luego sumarlos.
Ejemplo:
( ) 





+−+−−−− xxxxxx
2
3
3
7
2354 2324
3
2
7
3
19
2
____________________
2
3
3
7
2
354
234
23
24
−−−+−
+−+
−−−−
xxxx
xxx
xxx
( ) 





+−−−−−− xxxxxx
2
3
3
7
2354 2324
3
2
13
3
5
2
____________________
2
3
3
7
2
354
234
23
24
−−−−−
−+−+
−−−−
xxxx
xxx
xxx

6. Multiplicación de polinomios
Se multiplican todos los términos de un polinomio por todos los
términos del otro.
Ejemplo:
( ) ( )521543 224
−⋅−−+ xxxx
_________________
52
1543
2
24
−
−−+
x
xxx
5252015 24
++−− xxx
2346
21086 xxxx −−+
525221076
___________________________
2346
++−−− xxxxx

7. Consiste en aplicar la propiedad distributiva en sentido inverso, es
decir:
( )cbacaba ±⋅=⋅±⋅
Ejemplo:
Saca factor común en:
=+− xyyxyx 31512* 2322
=⋅⋅+⋅⋅⋅⋅⋅⋅−⋅⋅⋅⋅⋅⋅= yxyyxxxyyxx 353322
( )1543 2
+−⋅= yxxyxy
Extraer factor común

8. 127752 23
+++− xxxx
x10+
x2x2
División de dos polinomios
3
2x
2
6x− 2
6x−
3
2x−
2
x
2
x−
=
Multiplico y cambio
el signo
Sumo
2
6x+ x3+
5+x10+
= x3−
=
5−x10−
2+ Resto
Cociente
Ejemplo:
*Nota: Como en cualquier división, se cumple que:
D(x) = d(x) · C(x) + R(x)

9. Si no te ha quedado claro, puedes ver el siguiente vídeo pinchando sobre él.
http://www.youtube.com/watch?v=inuImtZHQjo

10. Ejemplo:
( ) ( )3:762 234
−−+− xxxx2 6− 1+ 0 7− 3
2
6
Bajo
Multiplico 0
0
1+
3+
Sumo SumoSumoSumo
3+
9+
2+ Resto
Cociente 32 3
++ xx
(Comencemos)
(Interpretemos esto)
Regla de Ruffini
Es un método que sirve para dividir polinomios utilizando sólo los
coeficientes, pero únicamente se puede utilizar cuando el polinomio
divisor es de la forma: ( x – a ), donde “a” es un número entero.
*Nota: Como el divisor tiene grado 1, el cociente siempre tendrá un
grado menos que el dividendo, y el resto será un número (grado 0).

11. Si no te ha quedado claro, puedes ver el siguiente vídeo pinchando sobre él.
http://www.youtube.com/watch?v=Rp3LEbCfNFs&feature=relmfu

12. Potencias. Productos notables
Hay 3 productos notables:
1) Cuadrado de una suma
( ) 222
2 bbaaba +⋅⋅+=+
Demostración:
( ) =+
2
ba ( ) ( ) =+⋅+ baba =⋅+⋅+⋅+⋅ bbabbaaa
22
2 bbaa +⋅⋅+=
2) Cuadrado de una diferencia
( ) 222
2 bbaaba +⋅⋅−=−
Demostración:
( ) =−
2
ba ( ) ( ) =−⋅− baba =⋅+⋅−⋅−⋅ bbabbaaa
22
2 bbaa +⋅⋅−=

13. 3) Suma por diferencia
( ) ( ) 22
bababa −=−⋅+
Demostración:
( ) ( ) =−⋅+ baba =⋅−⋅+⋅−⋅ bbabbaaa 22
ba −
*Nota: Para realizar cualquier otra potencia, multiplicaremos la base
tantas veces como indique el exponente.
Ejemplo:
( ) =+
2
23 yx ( ) ( ) =+⋅⋅+
22
22323 yyxx 22
4129 yxyx ++
( ) =−
23
2x ( ) ( ) =+⋅⋅−
2323
222 xx 44 36
+− xx
=





−⋅





+
3
2
3
2
xx
=





−
2
2
3
2
x
9
4
2
x
−
( ) =+
3
32x ( ) ( ) ( ) =+⋅+⋅+ 323232 xxx
( ) ( ) =+⋅++= 329124 2
xxx 2754368 23
+++ xxx

14. Descomposición factorial de polinomios
Se llama raíz o cero de un polinomio P(x) al número “a” tal que:
P(a) = 0
Ejemplos:
* tiene como raíces: x = 1, y x = 2, porque:23)( 2
+−= xxxP
02642232)2(
02312131)1(
2
2
=+−=+⋅−=
=+−=+⋅−=
P
P
* tiene como raíces: x = 0, y x = – 5, porque:xxxP 5)( 2
+=
( ) ( ) ( ) 02525555)5(
000050)0(
2
2
=−+=−⋅+−=−
=+=⋅+=
P
P
Descomponer un polinomio consiste en escribirlo como producto de
factores primos (polinomios de grado 0 ó 1).

15. Propiedades:
1.- Todas las raíces enteras de un polinomio P(x) son siempre
divisores del término independiente.
Ejemplos:
* tiene como posibles raíces enteras:
1, –1, 2, –2 que son los divisores del termino independiente (+2).
* tiene como posibles raíces enteras:
1, –1, 2, –2, 3, –3, 6, –6 que son los divisores del termino independiente (+6).
23)( 2
+−= xxxP
65)( 2
++= xxxP
2.- El resto de la división P(x) : (x – a) es el valor numérico P(a).
(Teorema del resto)
Ejemplos:
* Si entonces,
 División exacta
 División no exacta
23)( 2
+−= xxxP
( ) 02642232)2(2:)(Re 2
=+−=+⋅−=→− PxxPdesto
( ) ( ) ( ) 202992333)3(3:)(Re 2
=++=+−⋅−−=−→+ PxxPdesto

16. 3.- Si un número “a” es raíz del polinomio P(x), entonces, (x – a)
es un factor primo de P(x). (Teorema del factor)
(Esto se deduce de la propiedad anterior y de la definición de raíz, pues el resto de P(x) : (x –
a) es el valor numérico P(a), y como “a” es raíz, entonces dicho resto P(a) = 0, lo cual quiere
decir que la división es exacta y por lo tanto, (x – a) es divisor o factor primo de P(x) ).
(Por lo tanto, para encontrar los factores primos de un polinomio, bastará con encontrar sus
raíces.)
Ejemplos:
* tiene como raíces enteras: x =1, x = 2.
Por tanto, (x – 1) y (x – 2) son dos factores del polinomio P(x).
23)( 2
+−= xxxP
4.- Todo polinomio tiene tantas raíces como su grado, y por lo
tanto tantos factores como su grado. (Teorema fundamental del álgebra)
Ejemplos:
* tiene sólo dos raíces, que son: x =1, x = 2. Por lo tanto,
(x – 1) y (x – 2) son los dos únicos factores del polinomio P(x), es decir:
23)( 2
+−= xxxP
( ) ( )21)( −⋅−= xxxP
* tiene sólo tres raíces, que son: x =0, x = 2, x = –2. Por lo tanto,
(x) (x – 2) y (x + 2) son los tres únicos factores del polinomio P(x), es decir:
xxxP 4)( 3
−=
( ) ( )22)( +⋅−⋅= xxxxP

17. stoRe
031
31
321
1
⇓
−
Veamos los pasos a seguir para hacer la descomposición:
1º) Sacar factor común. (Si se puede)
2º) Ver si es un producto notable.
3º) Buscar las raíces, y así tendremos los factores.
Ejemplos:
*
*
* no se puede sacar factor común ni es un producto notable.
Posibles raíces enteras +1,–1, +3,–3.
Como: P(1) = 12
+ 2 .
1 – 3 = 0, entonces, x = 1 es una raíz, por tanto, (x – 1) es un factor.
Para encontrar el otro factor, hacemos la división: P(x) : (x – 1) por Ruffini.
xxxP 63)( 2
+=  → comúnfactorsacando ( )23)( +⋅= xxxP
9)( 2
−= xxP  → notableproducto ( ) ( )33)( −⋅+= xxxP
32)( 2
−+= xxxP
( )3+ → xCOCIENTE
( ) ( )31)( +⋅−= xxxPResultado:
Descomponer un polinomio consiste en escribirlo como producto de
factores primos (polinomios de grado 0 o 1).

18. stoRe
012
12
112
1
⇓
−−
Ejemplos:
*
*
* (no se puede sacar factor común ni es un producto notable.)
Posibles raíces enteras +1,–1.
Como: P(1) = 2 .
12
– 1 – 1 = 0, entonces, x = 1 es una raíz, por tanto, (x – 1) es un factor.
(Para encontrar el otro factor, hacemos la división: P(x) : (x – 1) por Ruffini.)
xxxP 22)( 3
−=  → comúnfactor ( ) ( )112)( −⋅+⋅= xxxxP
xxxxP 96)( 23
+−= → ( )2
3)( −⋅= xxxP
12)( 2
−−= xxxP
( )12 + → xCOCIENTE
( ) ( )121)( +⋅−= xxxPResultado:
( )12)( 2
−⋅= xxxP  → notpro
→ ( )96)( 2
+−⋅= xxxxP

19. 0213
213
2323
1
−
−
−−
Ejemplos:
* (no se puede sacar factor común ni es un producto notable.)
Posibles raíces enteras +1,–1,+2,– 2.
(Buscamos raíces y sólo encontramos dos, por tanto, sólo tendremos dos factores.)
Como: P(1) = 3 .
13
– 2 .
12
– 3 .
1 + 2 = 0  x = 1 es una raíz  (x – 1) es un factor.
Como: P(–1) = 3 .
(–1)3
– 2.
(–1)2
– 3 .
(–1)+ 2 = 0  x = – 1 es una raíz  (x + 1) es un factor.
(Para encontrar el otro factor, hacemos las divisiones por Ruffini.)
2323)( 23
+−−= xxxxP
( )23 2
−+
⇓
xx
( ) ( ) ( )2311)( −⋅+⋅−= xxxxPResultado:
023
23
213
1
−
−
−
−
( )23 −
⇓
x

20. La descomposición factorial se usa para:
•Simplificar fracciones algebraicas.
•Sumar o restar fracciones algebraicas (mcm).
•Resolver ecuaciones e inecuaciones de grado mayor de dos.
Ejemplos:
44
22
23
23
+−−
−−+
xxx
xxx ( ) ( ) ( )
( ) ( ) ( )221
211
+⋅−⋅−
+⋅+⋅−
=
xxx
xxx
Descompongo los polinomios.
( )
( )2
1
−
+
=
x
x
Simplifico.
Simplifica la fracción algebraica:

21. Ejercicios:
Obtén el cociente y el resto de las siguientes divisiones.
( ) ( )2:354) 23
+−−−− xxxxa
( ) ( )4:6) 23
+−+− xxxb



=
−−−=
5)(R
12)(
.
2
x
xxxC
Sol



=
−+−=
74)(R
205)(C
.
2
x
xxx
Sol
( ) ( )12:82) 235
+−−−+ xxxxxc 


−=
+++=
1610)(R
852)(C
.
23
xx
xxxx
Sol
( ) ( )153:352173) 2234
−+−+−− xxxxxxd



−=
−=
2)(R
4)(C
.
2
xx
xxx
Sol

22. Ejercicios:
Obtén el cociente y el resto de las siguientes divisiones.
( ) ( )2:354) 23
+−−−− xxxxb
( ) ( )1:23) 24
−−− xxxxc
( ) ( )4:6) 23
+−+− xxxd
( ) ( )3:652) 34
+−+ xxxe



=
−−−=
5)(R
12)(
.
2
x
xxxC
Sol



=
++=
0)(R
233)(C
.
23
x
xxxx
Sol



=
−+−=
74)(R
205)(C
.
2
x
xxx
Sol



=
−+−=
21)(R
932)(C
.
23
x
xxxx
Sol
( ) ( )2:2523) 24
−−+− xxxxa



=
+++=
48)(R
251063C(x)
.
23
x
xxx
Sol

23. Factoriza:
Ejercicios: (Resueltos)
xxa 102) 2
− ( )52 −⋅= xx Saco factor común.
19) 2
−xb ( ) ( )1313 −⋅+= xx Producto notable.
xxxc 12123) 23
+− ( )443 2
+−⋅= xxx
Saco factor común.
( )2
23 −⋅= xx Producto notable.
65) 2
−+ xxd No se puede sacar factor común.
Ni es un producto notable.
P.R.E. ±1, ±2, ±3, ±6
+1 es una raíz porque: P(1) = 12
+ 5 .
1 – 6 = 0  ( x – 1) es un factor.
( )⋅−= 1x
Hacemos Ruffini.
[ ]061
611
651 −
6+
⇓
x
( )6+x

24. Ejercicios:
Halla las raíces de los siguientes polinomios e indica sus factores:
4432)
152162)
273)
35)
54)
234
234
2
23
23
++−−
+−−+
++
−−−
−−
xxxxe
xxxxd
xxc
xxxb
xxxa ( ) ( ) ( )
( ) ( ) ( )
( ) ( )
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )2,2,1,1,2,2,1,1)
5,3,1,1,5,3,1,1)
3
1,2,
3
1,2)
3,1,1,3,1,1)
5,1,,5,1,0)
:
−−++→−−→
+−+−→−−→
++→−−→
−++→−−→
−+→−→
xxxxfactoresraícese
xxxxfactoresraícesd
xxfactoresraícesc
xxxfactoresraícesb
xxxfactoresraícesa
Soluciones

25. Ejercicios:
Realiza y simplifica:
90637
6032118
)
54
32
)
234
234
23
23
−++−
−++−
−−
−−
xxxx
xxxx
b
xxx
xxx
a ( )
( )
( )
( )3
2
)
5
3
)
:
+
+
−
−
x
x
b
x
x
a
Soluciones