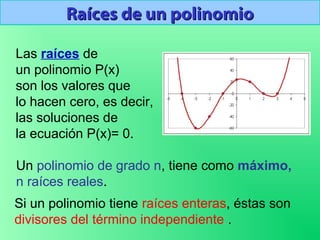
Este documento explica cómo dividir polinomios entre monomios y entre otros polinomios. Para dividir entre un monomio, se divide cada término del polinomio entre el monomio. Para dividir entre un polinomio, se siguen los pasos de ordenar los términos, dividir el primer término del dividendo entre el primero del divisor, multiplicar y restar, y repetir el proceso hasta que el grado del resto sea menor que el divisor. También presenta métodos como la regla de Ruffini y el teorema del resto y factor para

2. Cociente de un polinomio entre un monomioCociente de un polinomio entre un monomio
Para dividir un polinomio entre un monomio,
dividimos cada término del polinomio entre el
monomio.
Ej:
2245
32796)( xentrexxxxP +−=
( ) ( ) ( )=+−
=+−
222425
2245
3:273:93:6
3:)2796(
xxxxxx
xxxx
xentrexyyxxQ 257)( 3
−−=
( ) =
−
−
−
=−−
x
xy
x
yx
xxyyx
2
5
2
7
2:)57(
3
3
932 23
+− xx
yyx
2
5
2
7 2
+−

3. Cociente de polinomiosCociente de polinomios
Para dividir un polinomio entre un polinomio,
seguiremos los siguientes pasos:
1º) Ordenamos los términos del dividendo (si falta
algún término, se deja el hueco) y del divisor y los
dispondremos como una división normal.
xxxxxP 3011202)( 243
+−−+−=
23)( 2
−+= xxxQ
3
2x−4
x 2
11x− x30+ 20− 2
x x3+ 2−

4. Cociente de polinomios (II)Cociente de polinomios (II)
2º) Se divide el primer término del dividendo con el
primer término del divisor, así se obtiene el primer
término del cociente.
3
2x−4
x 2
11x− x30+ 20− 2
x x3+ 2−
2
x
3º) Se multiplica el primer término del cociente por
cada término del divisor y el producto pasa restando al
dividendo.
2
x4
x
234
2
2
23
23
xxx
x
xx
−+
×
−+
2
2x+3
3x−4
x−

5. Cociente de polinomios (III)Cociente de polinomios (III)
3
2x−4
x 2
11x− x30+ 20− 2
x x3+ 2−
4º) Se suman algebraicamente.
5º) Se divide el primer término del nuevo residuo, entre
el primer término del divisor, así obtenemos el segundo
término del divisor. Este segundo término se multiplica
por el divisor y se pasa restando al dividendo.
2
x
234
23 xxx +−−
2
9x−
x5−
xxx
x
xx
10155
5
23
23
2
+−−
−×
−+
x10−
2030 −+ x3
5x−
3
5x 2
15x+

6. Cociente de polinomios (IV)Cociente de polinomios (IV)
6º) Se repite el procedimiento hasta que
el grado del polinomio resto sea menor
que el grado del polinomio divisor.
3
2x−4
x 2
11x− x30+ 20− 2
x x3+ 2−
2
x
234
23 xxx +−−
203095 23
−+−− xxx
x5−
xxx 10155 23
−+
x20+
6+
12+
8−
2
6x− x18−
x2
20−2
6x

7. Cociente de polinomiosCociente de polinomios
3
2x−4
x 2
11x− x30+ 20− 2
x x3+ 2−
2
x x5− 6+
82 −x
Polinomio dividendo
=)(xD
3
2x−4
x 2
11x− x30+ 20− 2
x x3+ 2−
Polinomio divisor
Polinomio cociente
Polinomio resto
=)(xd
=)(xc
=)(xr
2
x x5− 6+
82 −x

8. Cociente de polinomiosCociente de polinomios
3
2x−4
x 2
11x− x30+ 20−
=)(xD
)23( 2
−+ xx
⋅)(xd )(xc )(xr+
)65( 2
+−⋅ xx =−+ )82( x
Prueba de la división:Prueba de la división:
Si el resto de la división es 0 (polinomio nulo), la división se
llama exacta y se dice que:
 El polinomio D(x) es divisible por d(x), o múltiplo de d(x).
 El polinomio d(x) es factor por D(x), o divisor de D(x).
=−+−+−+−++− 82121021815365 223234
xxxxxxxxx

9. 9
6x3
– 17x2
+ 15x – 8 3x – 4
Realiza la siguiente división:
-6x3
+ 8x2
2x2
- 9x2
+ 15x
- 3x
9x2
- 12x
+ 3x - 8
+ 1
-3x + 4
- 4
6x3
-17x2
+15x-8 = (3x-4)(2x2
-3x+1)-4
Cociente de polinomiosCociente de polinomios

10. Regla de RuffiniRegla de Ruffini
La regla de Ruffini es un algoritmo que permite
obtener fácilmente el cociente y el resto de la
división de un polinomio por un binomio de la
forma x-a.
1º) Ordenamos los términos del dividendo y del divisor.
532)( 23
−−+= xxxxD
1)( −= xxd

11. Regla de Ruffini (II)Regla de Ruffini (II)
532)( 23
−−+= xxxxD 1)( −= xxd
2º) Se colocan los
coeficientes de cada término.
Si no apareciese algún
término entre el de mayor
grado y el de menor se coloca
un 0.
2 1 3− 5−
3º) A la izquierda se pone el número que se resta a x en
d(x), en nuestro caso 1 y se baja el coeficiente del término
de mayor grado.
1
4º) Se multiplica el coeficiente que se ha bajado (2) por el
que se ha colocado a la izquierda (1). El resultado del
producto se coloca debajo del coeficiente del término
siguiente y se suman .
2
2
3

12. Regla de Ruffini (III)Regla de Ruffini (III)
5º) El resultado de la suma
se vuelve a multiplicar por el
número situado a la izquierda
y se repite el proceso.
2 1 3− 5−
1
2
2
3
3
0
0
5−
El último número (recuadro rojo) se corresponde
con el resto de la división mientras que el resto de
números de la fila inferior son los coeficientes del
cociente.
xxxc 32)( 2
+= 5)( −=xr
532)( 23
−−+= xxxxD 1)( −= xxd

13. Realiza las siguientes divisiones, indicando el cociente y el
resto obtenido:
Regla de Ruffini (III)Regla de Ruffini (III)
)3(:)113052() 23
++−− xxxxa
2 -5 -30 11
-3
2
-6
-11
33
3
-9
2
3112: 2
+− xxCociente
Resto: 2
)2(:)223() 4
−+−− xxxb
-1 0 0 -3 22
2
-1
-2
-2
-4
-4
-8
-11
-22
0
1142: 23
−−−− xxxCociente
Resto: 0
NOTA: El polinomio cociente es de un grado menor que el
dividendo

14. Teorema del restoTeorema del resto
Teorema del resto: El resto R de dividir un
polinomio P(x) entre x - a , es igual al valor
numérico del polinomio para x=a.
R = P(a)
Esto se deduce de la definición de división,
cuando el divisor d(x)=x-a:
RxCaxxP +⋅−= )()()(
Cuando x=a:
RaCaaaP +⋅−= )()()(
RaCaP +⋅= )(0)(
P(a)= R

15. Teorema del restoTeorema del resto
Sin efectuar la división, calcula el resto:
)3(:)113052() 23
++−− xxxxa
11)3(30)3(5)3(2)3( 23
+−⋅−−⋅−−⋅=−= PR
11)3(3095)27(2 +−⋅−⋅−−⋅=R
11904554 ++−−=R = 2
)2(:)223() 4
−+−− xxxb
22232)2( 4
+⋅−−== PR
22616 +−−=R = 0

16. El resto de dividir el polinomio P(x)=x3
-x2
+kx+2
entre x-1 es 6. Halla el valor de k:
Aplicación del Teorema del restoAplicación del Teorema del resto
62111)1( 23
=+⋅+−== kPR
Aplicando el teorema del resto: R=P(1)=6
6211 =++− k
4=k
P(x)=x3
-x2
+4x+2

17. Teorema del factorTeorema del factor
Teorema del factor: Un polinomio P(x) tiene
como factor x - a , si el valor numérico del
polinomio para x=a es 0.
Este resultado también proviene de la definición
de división, cuando el divisor d(x)=x-a:
RxCaxxP +⋅−= )()()(
Si el resto R=0:
)()()( xCaxxP ⋅−=
Esta relación indica que (x-a) es un factor o
divisor del polinomio P(x).

18. Comprobar si x+3 es un factor del polinomio
P(x)=x3
+2x2
-6x-9.
Aplicación del Teorema del factorAplicación del Teorema del factor
Aplicando el teorema del factor, si R=P(-3)=0,
entonces x+3 será un factor de P(x):
9)3(6)3(2)3()3( 23
−−⋅−−⋅+−=−= PR
9181827)3( −++−=−= PR
03636)3( =−=−= PR
Entonces x+3 es un factor de P(x) x3
+2x2
-6x-9
porque el resto es 0.

19. Comprobar si x+3 es un factor del polinomio
P(x)=x3
+2x2
-6x-9, aplicando Ruffini:
1 2 -6 -9
-3
1
-3
-1
3
-3
9
0
)3()3( 2
+−⋅+ xxx=−−+ 962 23
xxx
=)(xD ⋅)(xd )(xc )(xr+

20. Raíces de un polinomioRaíces de un polinomio
Las raíces de
un polinomio P(x)
son los valores que
lo hacen cero, es decir,
las soluciones de
la ecuación P(x)= 0.
Un polinomio de grado n, tiene como máximo,
n raíces reales.
Si un polinomio tiene raíces enteras, éstas son
divisores del término independiente .

21. Raíces enteras de un polinomioRaíces enteras de un polinomio
Para hallar las raíces enteras de un polinomio, aplicaremos el
teorema del resto a los divisores del término independiente.
Si el resto es 0, diremos que ese número es raíz del
polinomio.
EJ: Calcula las raíces enteras del siguiente polinomio:
33)( 23
−−+= xxxxP
{ }3,1)3( ±±=−Div
=−−⋅+= 31131)1( 23
P
Las posibles raíces enteras serán:
⇒0 1 sí es raíz
=−−−−⋅+−=− 3)1()1(3)1()1( 23
P ⇒0 -1 sí es raíz
=−−⋅+= 33333)3( 23
P ⇒≠=−+ 04862727 3 NO es raíz
=−−−−⋅+−=− 3)3()3(3)3()3( 23
P ⇒0 -3 sí es raíz
Las raíces enteras de P(x) son 1, -1 y -3.

22. Raíces enteras de un polinomioRaíces enteras de un polinomio
Cuando un polinomio no tiene término independiente,
se debe extraer factor común de x, x2
, x3
....
La raíz de ese monomio extraído siempre será 0.
EJ: Calcula las raíces enteras del siguiente polinomio:
24
)( xxxP −=
{ }1)1( ±=−Div
=−= 11)1( 2
Q
Las posibles raíces enteras serán:
1 sí es raíz
=−−=− 1)1()1( 2
Q
⇒0
Las raíces enteras de P(x) son 0, 1 y -1.
)1()( 22
−⋅= xxxP 0 sí es raíz
doble
⇒0 -1 sí es raíz
)(xQ

23. Raíces enteras de un polinomioRaíces enteras de un polinomio
Existen polinomios que no tienen raíces enteras.
EJ: Calcula las raíces enteras del siguiente polinomio:
2)( 2
+= xxP
{ }2,1)2( ±±=Div
21)1( 2
+=P
Las posibles raíces enteras serán:
⇒≠ 0 1 NO es raíz
2)1()1( 2
+−=−P ⇒≠ 0 -1 NO es raíz
22)2( 2
+=P ⇒≠ 0 2 NO es raíz
2)2()2( 2
+−=−P ⇒≠ 0 -2 NO es raíz
P(x) no tiene raíces enteras.
Se llaman polinomios irreducibles.

24. Factorización de polinomiosFactorización de polinomios
Factorizar un polinomio es descomponerlo en 2 o más
polinomios de menor grado, de forma que su producto
sea el polinomio dado.
EJ: Factoriza el siguiente polinomio:
5117)( 23
+++= xxxxP
Se busca una raíz mediante la Regla de Ruffini, entre las
posibles raíces enteras: { }5,1)5( ±±=Div
1 7 11 5
1
1
1
8
8
19
19
24
1 NO es raíz

25. 1 7 11 5
-1
1
-1
6
-6
5
-5
0
-1 sí es raíz
)1()( += xxP )56( 2
++⋅ xx
5117)( 23
+++= xxxxP
Es necesario volver a probar
si -1 es raíz
-1
1
-1
5
-5
0
-1 sí es raíz
)1()( += xxP )1( +⋅ x )5( +⋅ x
No existe un método único para factorizar un polinomio.
Lo habitual es buscar una raíz a y expresarlo como x-a
multiplicado por el cociente.

26. PASOS PARA FACTORIZAR UN POLINOMIOPASOS PARA FACTORIZAR UN POLINOMIO
Factorización de polinomiosFactorización de polinomios
1.-Sacar factor común, si se puede.
2.- Buscar las raíces enteras, poco a poco, y vamos
descomponiendo el polinomo, hasta llegar a un polinomio
de 2º grado.
3.- Observar el polinomio de 2º grado y puede pasar:
a) Que sea una identidad notable. Lo factorizo usándola.
b) Que no lo sea. Resuelvo la ecuación de 2º grado que
sale al igualar a cero el polinomio.
4. Escribo la factorización del polinomio, multiplicando
por el coeficiente de mayor grado si es distinto de 1.