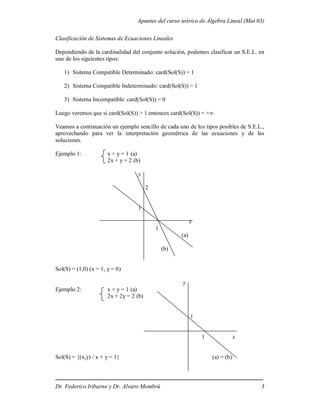
Este documento presenta un resumen del primer tema de un curso de álgebra lineal sobre sistemas de ecuaciones lineales. Introduce los sistemas de ecuaciones lineales y cómo se pueden clasificar dependiendo del número de soluciones. Explica que mediante transformaciones elementales es posible obtener sistemas equivalentes que pueden ser más fáciles de resolver.