El documento explica el Teorema del Valor Medio de Cálculo. Este teorema establece que si una función continua tiene una tangente no vertical en todo punto de un intervalo [A, B], entonces existe al menos un punto C en dicho intervalo donde la tangente es paralela a la recta que une los puntos A y B. La demostración usa el Teorema de Rolle para probar que existe un punto c donde la derivada de la función es igual a la pendiente de la recta secante entre los puntos A y B. Como ejemplo, se aplica el teorema

1. Universidad Técnica Particular de Loja Explicación y Aplicación del Teorema del Valor Medio CÁLCULO

2. Teorema del Valor Medio Es uno de los Teoremas más importantes dentro del Calculo Diferencial. En el lenguaje geométrico el teorema del Valor Medio es fácil de establecer y de comprender. Dice que si la gráfica de una función continua tiene una tangente no vertical en todo punto comprendido entre A y B, entonces hay por lo menos un punto C en la gráfica comprendida entre A y B en el que la tangente es paralela a la recta secante AB A B C

3. Demostración del Teorema Si una función f es continua en un intervalo cerrado [a, b] y diferenciable en su interior (a, b), entonces existe al menos un número c en cada (a, b). Observación: El teorema de Rolle es similar, se diferencian porque aqui no se exige f (a) = f (b). Si esto se diera se reduce al teorema de Rolle.

4. Demostración La expresión es la pendiente de la recta Secante que une los puntos (a, f (a)) y (b f (b)). Queremos probar que un punto x = c en la recta tangente tiene esa misma pendiente, o sea, es paralela a esa recta secante. a c b x y y=f(x) m=f’(c)

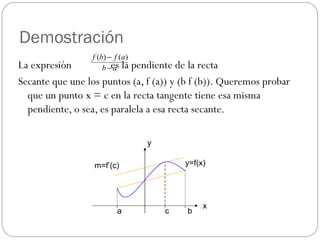
5. En primer lugar la recta secante que une a (a, f (a)) y (b f (b)) tiene pendiente . La ecuación de la recta es por lo tanto, Definimos la función inclinada g como la diferencia entre los valores de f y la secante. Como f es continua en [a, b] y derivable en (a, b), también g lo es. Además

6. Y porque Al ser g (a) = g (b), el teorema de Rolle existe un c en (a, b) tal que g’(c) = 0. Derivamos Luego despejamos f’(c) y llegamos al resultado antes mencionado:

7. Mediante el siguiente ejemplo, vamos a demostrar más detalladamente, en que consiste este teorema: Hallar el valor c que satisfaga la conclusión del teorema del valor medio para En el intervalo [0, 2]

8. Para hallar el número c haremos: Despejando Aplicando la formula general resolvemos: Myriam Sarango Karla Espinosa