El documento describe el método del trapecio para aproximar integrales definidas. El método del trapecio aproxima el área bajo una curva como el área de un trapecio formado por la función en los límites del intervalo y una línea recta entre ellos. Se provee un ejemplo numérico para ilustrar cómo aplicar la fórmula del método.

1. MÉTODOS NUMÉRICOS
Método del Trapecio
Iván A. Caicedo

2. Historia Método del Trapecio
La integración es un concepto muy aplicado en las matemáticas
avanzadas, en campos como el cálculo y el análisis numérico. En el
cálculo integral que es una de las ramas de las matemáticas, el
proceso de integración o antiderivación es muy común en las
ingenierías y se utiliza principalmente para el cálculo de áreas,
volúmenes de regiones y sólidos de revolución.
Asimismo, su uso se remonta desde los inicios de la humanidad con el
cálculo de las áreas de los terrenos para el cultivo de los granos.
Arquímedes fue uno de los primeros matemáticos en demostrar que el
área de un círculo era menor que el área del polígono circunscrito y
mayor que el área del polígono inscrito, utilizando el método de
exhausción propuesto por Eudoxo. El matemático determinó que
cuando el número de lados del polígono de igual radio era un número
muy grande, las áreas de ambos polígonos eran prácticamente
iguales. Arquímedes también utilizó este método de los polígonos
crecientes y decrecientes para demostrar que π era menor que 317 y
mayor que 31071.

3. El Método
En los cursos de Cálculo Integral aprendemos a calcular una integral definida de una función continua
haciendo uso del Teorema Fundamental del Cálculo que dice que si f(x) es una función continua en un
intervalo [a, b] y F(x) es una antiderivada de f(x) entonces:
∫baf(x)dx=F(b)−F(a)
El problema en la práctica se presenta, cuando se nos hace imposible mediante métodos analíticos
determinar la antiderivada requerida, aun cuando se trate de integrales aparentemente sencillas
como ∫21x31+x√dx, que son imposibles de resolver con el Teorema Fundamental del Cálculo.
En estos casos, debemos de recurrir a la integración numérica que permite obtener aproximaciones
bastantes exactas y que se pueden resolver con el uso de asistentes matemáticos
como Maxima, Derive, Mathematica, entre otros.
En este módulo nos referiremos a la regla del trapecio y a la regla de Simpson.

4. Regla del Trapecio
La regla del trapecio es uno de los métodos más utilizados para calcular
aproximaciones numéricas de integrales definidas. Es la primera de las fórmulas
cerradas de integración de Newton – Cotes, para el caso cuando el polinomio
interpolante es de grado uno.
Para el polinomio interpolante de primer grado se tiene:
A=∫baf(x)dx≅∫baf1(x)dx, donde
f1(x)=f(a)+f(b)−f(a)b−a(x−a)
Precisamente el área bajo la recta es una aproximación de la integral ∫baf(x)dx, es
decir queA=∫ba[f(a)+f(b)−f(a)b−a(x−a)]dx. Luego se tiene que la regla del trapecio
viene dada por la fórmula:
A=∫baf(x)dx≈(b−a)[f(a)+f(b)2]

5. Regla del Trapecio
El nombre regla del trapecio se debe a la interpretación geométrica que se hace de la fórmula. Cuando el
polinomio interpolante es de grado uno, su gráfica representa una línea recta en el intervalo [a, b] que es el área
del trapecio que se forma, como se muestra en la figura.

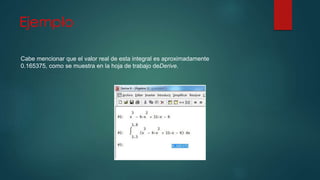
6. Ejemplo
Calcular la integral de f(x)=x3−6x2+11x−6, en el intervalo [1.3, 1.8] aplicando la regla del trapecio.
Solución
•Con la ayuda de una calculadora, evaluar la función en los extremos del intervalo f(1.3)=0.357, f(1.8)=0.192
•Calcular b−a=1.8−1.3=0.5
•Aplicar la fórmula de la regla del trapecio A=∫1.81.3(x3−6x2+11x−6)dx≅0.5[0.357+0.1922]=0.13725
En la siguiente figura se muestra la gráfica de la función construida con el software libre Winplot.

7. Ejemplo
Cabe mencionar que el valor real de esta integral es aproximadamente
0.165375, como se muestra en la hoja de trabajo deDerive.