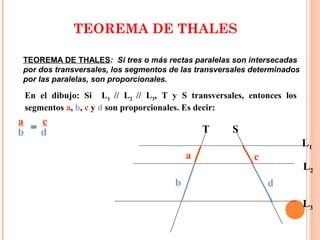
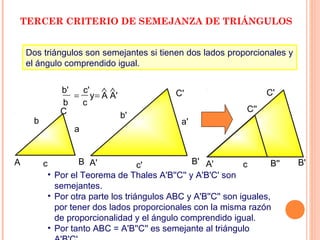
El documento presenta el Teorema de Tales, desarrollado por el matemático griego Tales de Mileto. Explica que el teorema establece que si tres o más rectas paralelas son cortadas por dos transversales, los segmentos de las transversales entre las paralelas son proporcionales. Además, introduce los conceptos de triángulos en posición de Tales y semejanza de triángulos, y proporciona ejemplos para aplicar el teorema en la resolución de problemas geométricos.

1. TEOREMA DE
THALES
APM

2. TEOREMA DE THALES. ÍNDICE
 Thales de Mileto.
 Origen del Teorema de Thales.
 Teorema de Thales.
 Ejercicio de aplicación 1.
 Ejercicio de aplicación 2.
 Triángulos en posición de Thales.
 Semejanza de triángulos.
 Primer criterio de semejanza de triángulos.
 Segundo criterio de semejanza de triángulos.
 Tercer criterio de semejanza de triángulos.
 Aplicaciones.

3. THALES DE MILETO
Nació alrededor del año 624 a.C.
en Mileto, Asia Menor (ahora
Turquía). Murió en el año 548 a.C.
Thales era un hombre que se
destacó en varia áreas:
comerciante, hábil en ingeniería,
Astronomía y Geometría.
Thales era considerado uno de
los siete sabios de Grecia.
THALES DE MILETO. BIOGRAFÍA

4. ORIGEN DEL TEOREMA DE THALES
• Se cuenta que comparando la
sombra de un bastón y la sombra de
las pirámides, Thales midió, por
semejanza, sus alturas respectivas.
La proporcionalidad entre los
segmentos que las rectas paralelas
determinan en otras rectas dio lugar
a lo que hoy se conoce como el
teorema de Thales.

5. ORIGEN DEL TEOREMA DE THALES
Puesto que los rayos del Sol inciden paralelamente sobre la Tierra,
los triángulos rectángulos determinados por la altura de la
pirámide y su sombra y el determinado por la altura del bastón y la
suya son semejantes.
Rayos solares
Pirámide
Podemos, por tanto, establecer la proporción:
S (sombra)
H(altura de la
pirámide)
s (sombra)
h (altura de bastón)
HS
= hs
De donde: H= h•S
s

6. TEOREMA DE THALES: Si tres o más rectas paralelas son intersecadas
por dos transversales, los segmentos de las transversales determinados
por las paralelas, son proporcionales.
En el dibujo: Si L1 // L2 // L3, T y S transversales, entonces los
segmentos a, b, c y d son proporcionales. Es decir:
T S
L1
L2
L3
a
a
b
b =
c
c
d
d
TEOREMA DE THALES

7. EJEMPLO DE APLICACIÓN 1
L1
L2
L3
En la figura L1 // L2 // L3 , T y S transversales,
calcula la medida del trazo x.
T
S
8
24
x
15
Ordenamos los datos en la proporción,
de acuerdo al teorema de Thales.
Es decir: 8
24 = x
15
Y resolvemos la proporción:
24 • x = 8 • 15
x =8 • 15
24
x = 5

8. EJEMPLO DE APLICACIÓN 2
En la figura L1 // L2 // L3 , T y S son transversales, calcula x y el trazo CD
Formamos la proporción:
32
= x+4
x+1
Resolvemos la proporción:
3(x + 1) = 2(x + 4)
3x + 3 = 2x + 8
3x - 2x= 8 - 3
x=5
L1
L2 L3
T
S
x+4
x+1
3 2
C
D
Luego, como CD = x + 4
CD= 5 + 4 = 9

9. TRIÁNGULOS EN POSICIÓN DE THALES
Dos triángulos están en posición de Thales cuando:
Tienen un ángulo común y los lados opuestos a dicho ángulo son paralelos.
Podemos ver ésto si trasladamos el triángulo
formado por el bastón, su sombra y los rayos
solares hacia el formado por la pirámide
S (sombra)
H(altura de la pirámide)
s (sombra)
h (altura de bastón)

10. SEMEJANZA DE TRIÁNGULOS
Dos triángulos en posición de Thales son semejantes.
A
De acuerdo a esto, en la figura BC// ED,
entonces, con los lados de los triángulos AED y
ABC ocurre:
E D
B C
AE
AB = ED
BC
O también:
AE
ED
= AB
BC
DEMOSTRACIÓN INTERACTIVA

11. SEMEJANZA DE TRIÁNGULOS
Dos triángulos son semejantes si tienen los lados proporcionales y
los ángulos iguales.
El cociente
a = b = c =
k
a ' b' c'
se llama razón de semejanza.

12. PRIMER CRITERIO DE SEMEJANZA DE TRIÁNGULOS
Dos triángulos son semejantes si tienen dos ángulos iguales.
Ù
Ù
Ù
Ù
Ù
A = A‘ y B = B‘ Þ C = C'
C
Ù
A B
C'
A' B'
C'
C''
A' B''
B'
• Por el Teorema de Tales A'B''C'' y A'B'C' son
semejantes.
• Por otra parte los triángulos ABC y A'B''C'' son iguales,
por tener un lado igual y los ángulos iguales.
• Por tanto ABC = A'B''C'' es semejante al triángulo
A'B'C'.

13. SEGUNDO CRITERIO DE SEMEJANZA DE TRIÁNGULOS
Dos triángulos son semejantes si tienen los lados proporcionales.
C
a
A B
C'
b'
C'
• Por el Teorema de Thales A'B''C'' y A'B'C' son
semejantes.
• Por otra parte los triángulos ABC y A'B''C'' son iguales,
por tener un lado igual y ser los lados de ambos
proporcionales a los del triángulo A'B'C' con la misma
razón de proporcionalidad.
• Por tanto ABC = A'B''C'' es semejante al triángulo
A'B'C'.
b
c A' B'
c'
a'
a ' = b' =
c'
a b c
A' B''
B'
C''

14. TERCER CRITERIO DE SEMEJANZA DE TRIÁNGULOS
Dos triángulos son semejantes si tienen dos lados proporcionales y
el ángulo comprendido igual.
b' c' Ù Ù
b c
C
a
A B
C'
b'
C'
• Por el Teorema de Thales A'B''C'' y A'B'C' son
semejantes.
• Por otra parte los triángulos ABC y A'B''C'' son iguales,
por tener dos lados proporcionales con la misma razón
de proporcionalidad y el ángulo comprendido igual.
• Por tanto ABC = A'B''C'' es semejante al triángulo
A'B'C'.
b
c A' B'
c'
a'
= y = A A'
A' B''
B'
C''
c

15. APLICACIONES
Problema 1: Calcula la altura del siguiente edificio:
x
5
3 12
Escribimos la proporción:
35
= 15
x
Y resolvemos la proporción:
3 • x = 5 • 15
x = 75
3
x = 25
Por que 3+12=15

16. APLICACIONES
Problema 2: En el triángulo ABC, DE//BC , calcule x y el trazo AE.
C
D 12
8
A x+3 E
x
B
Formamos la proporción:
8
x+3 = 12
2x+3
Por que
x+3+x = 2x+3
Resolvemos la proporción:
8(2x + 3) = 12( x + 3)
16x + 24 = 12x + 36
16x – 12x = 36 – 24
4x = 12
x = 12 = 3
4
Por lo tanto, si AE = x + 3 = 3 + 3 = 6

17. HASTA PRONTO, CHAVALES.
ESPERO QUE HAYÁIS APRENDIDO MUCHO.
COMPROBAD VUESTRO APRENDIZAJE CON
LAS ACTIVIDADES QUE APARECEN EN LA
PÁGINA WEB.
¡¡¡¡ ADIOS !!!!