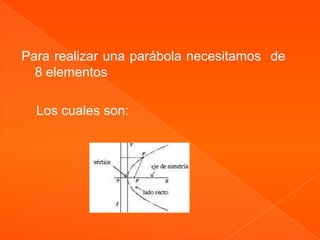
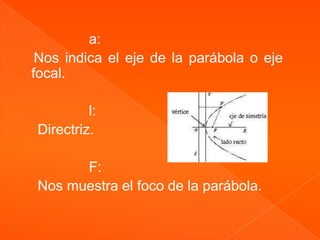
Este documento explica la teoría de las parábolas. Una parábola es el conjunto de puntos que equidistan de un foco y una directriz. Se explican los elementos necesarios para graficar una parábola y sus ecuaciones dependiendo de la posición del vértice.

1. Teoría
de la
Parábola

2.  Una parábola es el conjunto de puntos
en el plano que se mueve de tal manera
que siempre equidistan de un punto fijo
y una recta fija, a los cuales se les llama
foco y directriz.

3.  Nos ayudará a formar correctamente la
parábola dentro de un plano
cartesiano, si alguno de estos elementos
no coinciden como deben de
ser, entonces nos daremos cuenta de
que hicimos algo incorrecto.

4. Para realizar una parábola necesitamos de
8 elementos
Los cuales son:

5. a:
Nos indica el eje de la parábola o eje
focal.
l:
Directriz.
F:
Nos muestra el foco de la parábola.

6. v
El vértice o punto en el que se unirá la
parábola con el eje focal.
BB
Cuerda(une dos puntos de la parábola).
DD
Cuerda focal(pasa por el foco)

7. LL
Lado recto (cuerda focal
perpendicular al eje focal)
FP
Radio Vector

8.  Una parábola puede estar con el vértice
en el punto de origen o fuera de él.
 En cada una existen ecuaciones
diferentes.

9.  Una parábola con vértice en el origen se
puede encontrar en eje “x” o en eje “y”.
 Esto depende del valor del foco, si el foco
nos da valor en la coordenada `x la parábola
queda de forma horizontal y eso nos dice que
la ecuación a seguir será eje “x”, de lo
contrario, si nos da un valor en eje `y la
parábola quedarà verticalmente y la ecuación
que se utilizarà será la del eje “y”.

10.  v (0,0)
 F (P,0) para obtener valor de P
 LR= 4P nos indica el tamaño de la
 directriz
 x= -P coordenada de la directriz
 y2=4Px ecuación para obtener las
 coordenadas de la gràfica
 P>0 : abre a la derecha
 P<0 : abre a la izquierda

11. V(0,0) F(P,0) X=-P
X= -(-3)
F(-3,0) P=-3 X= 3
LR= 4P y2=4Px
F(P,0) y2=4(-3)x
LR= 4(-3) y2= -12x
LR= 4P LR= 12 y=+- -12x
X=-P
y2=4Px

12.  v (0,0)
 F (0,P) para obtener valor de P
 LR= 4P nos indica el tamaño de la
 directriz
 y= -P coordenada de la directriz
 x2=4Py ecuación para obtener las
 coordenadas de la grafica
 P>0 : abre hacia arriba
 P<0 : abre hacia abajo

13. y= -P
 v (0,0) F (0,P) y= -(2)
 F (0,2) P=2 y= -2
 F (0,P) LR= 4P x2=4Py
LR= 4(2) x2=4(2)y
 LR= 4P
LR=8 x2=8y
 y= -P
x2=+- 8y
 x2=4Py

14. Con el vértice en el punto de origen y
teniendo el valor del foco se puede
encontrar la parábola
Pero también se pueden tener otros
valores en lugar de el foco, en estos casos
se utilizan las mismas ecuaciones pero
despejando los valores que te dè el
problema.

15. Las ecuaciones de una parábola con vértice
fuera del punto de origen se dividen en eje
“x” y eje “y” al igual que la parábola con
vértice en el origen, solo que las
ecuaciones de cada una de estas son
diferentes.
Ahora nos daremos cuenta de cuando es
eje “x” o “y” según la posición en la que
quede la línea que une al foco con el
vértice (eje de la parábola).

16.  V(h,k) valor del vértice
 F(h+P,k) para obtener valor de P
 LR= 4P tamaño de directriz
 x=h-P coordenada de la
 directriz
 (y-k)2=4P(x-h) ecuación para obtener
 las coordenadas de la
 gràfica.

17.  V(-5,2) V(-5,2) x=h-p
V(h,k) y=-5-3
 F(-2,2)
h=-5 y=-8
k=2
 Eje “x”
 V(h,k) F(-2,2) (y-k)2=4P(x-h)
 F(h+P,k) F(h+P,k) (x-2)2= 4(3)(y-(-5))
 LR= 4P F((h+P=-2),2)) (X-5)2=-12(y+5)
 x=h-P -5+P=-2 (X-2)=+- 12(y+5)
P=-2+5
 (y-k)2=4P(x-h) P=3 X=+2 +- 12(y+5)
LR= 4P
LR= 4(3)
LR=12

18.  V(h,k) valor del vértice
 F(h,P+k) para obtener valor de P
 LR= 4P tamaño de directriz
 y=k-P coordenada de la directriz
 (x-k)2=4P(y-h) ecuación para obtener las
coordenadas de la gráfica

19.  V(4,8) V(4,8) y=k-p
 F(4,2) V(h,k) y=8-(-6)
h=4 y=14
k=8
 Eje “y”
 V(h,k) F(4,2)
(x-k)2=4P(y-h)
 F(h,P+k) F(h,P+k)
(x-8)2= 4(-6)(y-4)
 LR= 4P F(4,(P+k=2)) (X-8)2=-24(y-4)
 y=k-P P+8=2 (X-8)=+- -24(y-4)
P=2-8
 (x-k)2=4P(y-h) P=-6 X=+8 +- -24(y-4)
LR= 4P
LR= 4(-6)
LR=24

20.  Nuevamente se pueden dar valores
diferentes en lugar de utilizar el foco o el
vértice y de igual manera se tendrán que
manejar correctamente solo las ecuaciones
que te dan, para poder llegar a cada valor
necesario.