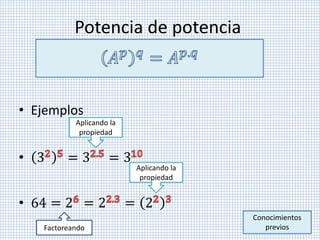
El documento describe los conocimientos previos necesarios para trabajar con raíces. Explica cómo obtener la mínima expresión de un radical mediante la factorización del radicando, la aplicación de propiedades como la raíz de raíz y la distribución de la radicación sobre la multiplicación, y el uso de potencias de potencias. Proporciona varios ejemplos para ilustrar cada paso del proceso de simplificación.

1. Radicales
Conocimientos previos - -
Obtención de la mínima expresión

2. Los números compuestos admiten
descomposición en factores primos
• Ejemplos:
• 48 = 24
. 3 60 = 22
. 3.5 100 = 22
.52
Conocimientos
previos

3. Producto de potencias de igual base
• Ejemplos:
• 7 . 7 = 7 = 7
(ya que =7.7.7.7
7
. 7.7.7.7.7
7
=7.7.7.7.7.7.7.7.7
7
)
• 2 . 2 . 2 = 2 11
• 3 =
3 = 35
. 33
3 = 32
. 36
.
Conocimientos
previos

4. cociente de potencias de igual base
• Ejemplos:
• 7 7 = 7 = 7
(ya que =
7.7.7.7.7.7
7 𝟔
7.7.7.7
7
=7.7
7`𝟐
)
•
Conocimientos
previos

5. • Ejemplos
• 3 = 3 = 3
• 64 = 2 = 2 = 2
Potencia de potencia
Conocimientos
previos
Aplicando la
propiedad
Factoreando
Aplicando la
propiedad

6. La radicación se distribuye respecto a
la multiplicación:
•Ejemplos
•
4
. 16 =
4
16 = .2 = 6
•
3
.5 =
3
5 =
3
5
Conocimientos
previos

7. Raíz de raíz
• Ejemplos
• 7 = 7 = 7
• 7 =
7 = 7
7 = 7
… … … … … … Conocimientos
previos

8. Simplificación
•Ejemplo:
• 243 = 3 = 3
Conocimientos
previos

9. Conocimientos previos
Los números compuestos admiten
descomposición en factores primos
Producto de potencias de igual base
• Potencia de potencia I
• Raíz de raíz
• La radicación se distribuye respecto a la
multiplicación
• Los operaciones inversa aplicadas simultáneamente
se Simplifican
• Mínima Expresión de un Radical

10. Radicales
Un radical es cualquier raíz indicada de una expresión.
• −6
𝟑
𝟐𝒙
coeficiente Sub radical o
radicando
• 3 𝟐𝟓 = 3.5=15 • 2
𝟒
𝟕
Radical racional Radical
irracional

11. Mínima Expresión de un Radical
El objetivo es obtener una expresión donde el
radical tenga la menor cantidad de factores
Ejemplo1:
•
3
•=
3
2
•= 2
•= 2
•= 4
𝐟 𝐚 𝐜 𝐭 𝐨 𝐞 𝐚 𝐧 𝐝 𝐨 𝐝 𝐞 𝐫 𝐚 𝐝 𝐢 𝐜 𝐚 𝐧 𝐝 𝐨 𝟔 𝟒 = 𝟐 𝟔
𝒆𝒍 𝒆𝒙𝒑𝒐𝒏𝒆𝒏𝒕𝒆 𝟔 = 𝟐. 𝟑 𝒔𝒆 𝒑𝒖𝒆𝒅𝒆 𝒆𝒙𝒑𝒓𝒆𝒔𝒂𝒓 𝒄𝒐𝒎𝒐
𝒑𝒐𝒕𝒆𝒏𝒄𝒊𝒂 𝒅𝒆 𝒑𝒐𝒕𝒆𝒏𝒄𝒊𝒂
𝐒 𝐢 𝐦 𝐩 𝐥 𝐢 𝐟 𝐢 𝐜 𝐚 𝐧 𝐝 𝐨
Conocimientos
previos

12. Conocimientos
previos
Mínima Expresión de un Radical
El objetivo es obtener una expresión donde el
radical tenga la menor cantidad de factores
Ejemplo2:
•
6
125 =
•=
6
53 =
•=
2
5 =
•= 5
𝐟 𝐚 𝐜 𝐭 𝐨 𝐫 𝐞 𝐚 𝐧 𝐝 𝐨 𝐞 𝐥 𝐫 𝐚 𝐝 𝐢 𝐜 𝐚 𝐧 𝐝 𝐨 𝟏 𝟐 𝟓 = 𝟓 𝟑
𝑬 𝒍 𝒊 𝒏 𝒅 𝒊 𝒄 𝒆 𝟔 = 𝟑 . 𝟐 → 𝑹 𝒂 í 𝒛 𝒅 𝒆 𝑹 𝒂 í 𝒛
𝑺 𝒊 𝒎 𝒑 𝒍 𝒊 𝒇 𝒊 𝒄 𝒂 𝒄 𝒊 ó 𝒏

13. Mínima Expresión de un Radical
El objetivo es obtener una expresión donde el
radical tenga la menor cantidad de factores
Ejemplo3:
•
3
=
•=
3
=
•= 2 .
3
5 =
•= 2
3
5
Conocimientos
previos
𝐟 𝐚 𝐜 𝐭 𝐨 𝐫 𝐞 𝐚 𝐧 𝐝 𝐨 𝐞 𝐥 𝐫 𝐚 𝐝 𝐢 𝐜 𝐚 𝐧 𝐝 𝐨
𝒅 𝒊 𝒔 𝒕 𝒓 𝒊 𝒃 𝒖 𝒕 𝒊 𝒗 𝒂
𝑺 𝒊 𝒎 𝒑 𝒍 𝒊 𝒇 𝒊 𝒄 𝒂 𝒄 𝒊 ó 𝒏
4 0 2
2 0 2
1 0 2
5 5
1
𝟒 𝟎 = 𝟐 𝟑 . 𝟓

14. Mínima Expresión de un Radical
El objetivo es obtener una expresión donde el
radical tenga la menor cantidad de factores
Ejemplo4:
•
3
32 =
•=
3
2 =
•=
3
2 . 2 =
•= .
3
22 =
3
4
Conocimientos
previos
F 𝐚 𝐜 𝐭 𝐨 𝐫 𝐞 𝐚 𝐧 𝐝 𝐨 𝐞 𝐥 𝐫 𝐚 𝐝 𝐢 𝐜 𝐚 𝐧 𝐝 𝐨 𝟑 𝟐 = 𝟐 𝟓
𝒅 𝒊 𝒔 𝒕 𝒓 𝒊 𝒃 𝒖 𝒕 𝒊 𝒗 𝒂
𝑺 𝒊 𝒎 𝒑 𝒍 𝒊 𝒇 𝒊 𝒄 𝒂 𝒄 𝒊 ó 𝒏
3 2 2
1 6 2
8 2
4 2
2 2
1
𝑷 𝒆 𝒓 𝒐 𝒄 𝒐 𝒎 𝒐 𝒆 𝒍 𝒓 𝒂 𝒅 𝒊 𝒄 𝒂 𝒍 𝒕 𝒊 𝒆 𝒏 𝒆 𝒊 𝒏 𝒅 𝒊 𝒄 𝒆 𝟑
p a ra p o der s i m pli f icar a g rupamos d e a
t res f a c t o r e s