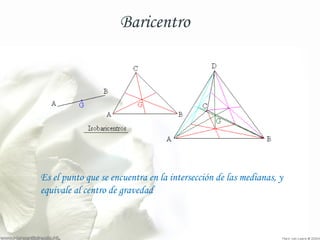
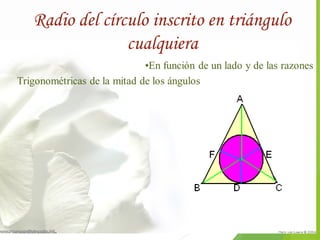
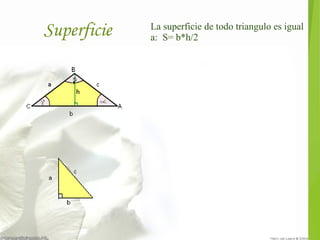
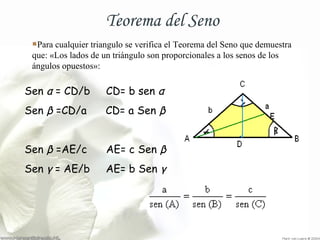
Este documento presenta varias fórmulas y teoremas relacionados con los triángulos. Explica cómo calcular la superficie de un triángulo y la fórmula de Herón. También describe el teorema del seno, el teorema del coseno, el teorema de Pitágoras y propiedades de los triángulos como la suma de sus ángulos internos. Finalmente, define conceptos como el ortocentro, el baricentro y el radio del círculo inscrito.

1. Presentación de algunas
formulas de los triángulos:

2. La superficie de todo triangulo es igual
a: S= b*h/2 Superficie

3. Formula de Herón
•Si conocemos las longitudes de los lados del triángulo (a, b, c) es
posible calcular la superficie empleando la fórmula de herón
viene dada por:
Donde p es el semiperimetro

4. Demostración
Supongamos un triángulo de lados a, b, c cuyos ángulos opuestos a
cada uno de esos lados son A, B, C. Entonces tenemos que:
Por el teorema del coseno :
La altura de un triángulo de base a tiene una
longitud bsen( C), por lo tanto:

5. Propiedades del triángulo
•La suma de las longitudes de dos de sus lados es siempre mayor
que la longitud del tercer lado.
•La suma de todos los ángulos de sus vértices, en un plano, es igual
a 180°.

6. Teorema del Seno
Para cualquier triangulo se verifica el Teorema del Seno que demuestra
que: «Los lados de un triángulo son proporcionales a los senos de los
ángulos opuestos»:
Sen α = CD/b CD= b sen α
Sen β =CD/a CD= a Sen β
Sen β =AE/c AE= c Sen β
Sen γ = AE/b AE= b Sen γ

7. Teorema del coseno
•Relaciona el tercer lado de un triángulo con los dos primeros y
con el coseno del ángulo formado por estos dos lados.
a² =CD²+ DB²
CD²= b²- AD²
a² = b² - AD²+ DB²
a²= b² - AD²+C² - 2DC +AD²
a² =b²+ c²-2c*AD
a² = b² + c²- 2c* b cos A
b² = a² + c² –2ac cosβ
c² = a² + b² –2ab cos C

8. Teorema de Pitágoras
•El Teorema de Pitágoras establece que en un triángulo rectángulo
la suma de los cuadrados de los catetos es igual al cuadrado de la
hipotenusa:
c² =a²+ b² - 2ab cos90º

9. Teorema
Sea C un punto de la circunferencia de diámetro [AB], distinto de A
y de B. Entonces el ángulo ACB es recto.
Prueba: OA = OB = OC = r, radio del círculo.
Por lo tanto OAC y OBC son isósceles. La
suma de los ángulos del triángulo ABC vale
2α + 2β = π (radianes). Dividiendo por dos, se
obtiene
Además dice que la bisectriz de un triángulo corta al lado opuesto del ángulo
con la bisectriz en dos segmentos proporcionales Hipotenusa (al cuadrado) =
C(Al cuadrado) + C(Al cuadrado) En conclusión se forma un triangulo
rectangulo

10. Ortocentro
•Se denomina ortocentro al punto donde se
cortan las tres alturas de un triángulo.
El término deriva de orto, recto, en
referencia al ángulo formado entre las bases
y las alturas.
•El ortocentro se encuentra dentro del triángulo si éste es acutángulo,
coincide con el vértice del ángulo recto si es rectángulo, y se halla
fuera del triángulo si es obtusángulo
•El único caso en que los centros coinciden en un único punto es
en un triángulo equilátero.

11. Baricentro
Es el punto que se encuentra en la intersección de las medianas, y
equivale al centro de gravedad

12. Radio del círculo inscrito en triángulo
cualquiera

13. Muchas gracias.
 Luis Pauta-