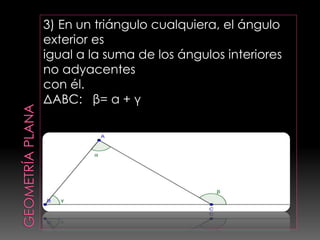
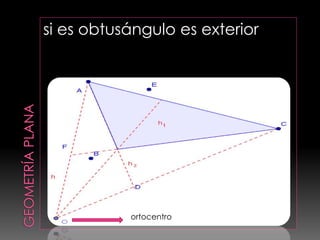
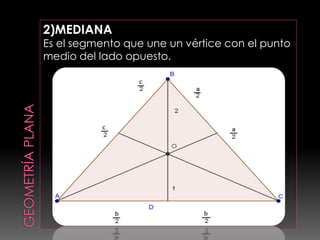
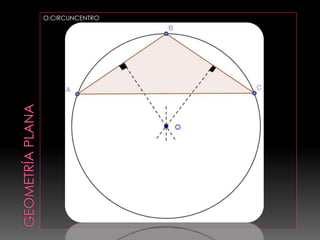
Este documento presenta conceptos básicos de geometría, incluyendo definiciones de puntos, líneas, planos, ángulos y figuras geométricas como triángulos. Explica propiedades de ángulos, líneas principales de triángulos como alturas, medianas y bisectrices, y teoremas relacionados con igualdad, semejanza y relaciones métricas en triángulos.

2. Es la parte de la Matemática
Elemental que trata de
las propiedades y medidas de
la extensión. La
Geometría parte de ciertos
conceptos primitivos
dados intuitivamente, tales
como: punto, recta y
plano. Se divide en GEOMETRÍA
PLANA Y
GEOMETRÍA DEL ESPACIO.

3. ÁNGULOS:
TEOREMAS BÁSICOS

4. ÁNGULOS
TEOREMAS BÁSICOS
1) La suma de los ángulos consecutivos
formados
alrededor de un punto y a un mismo lado de
una
recta es 180°.
Punto O: α + β + γ + δ = 180°

5. 2) En todo triángulo, la suma de los
ángulos internos
es igual a 180°.
Δ ABC: α + β + γ = 180°

6. 3) En un triángulo cualquiera, el ángulo
exterior es
igual a la suma de los ángulos interiores
no adyacentes
con él.
ΔABC: β= α + γ

7. TEOREMAS AUXILIARES

8. TEOREMA 1.-
En todo cuadrilátero cóncavo, el ángulo
exterior
convexo, es igual a la suma de los ángulos
interiores
convexos:
Δ BACD: α = β+ ε + δ

9. TEOREMA 2.-
El ángulo formado por dos bisectrices
interiores
de un triángulo, es igual a noventa
grados más la
mitad del tercer ángulo:
ΔABC: α = 90° + ε
2

10. TEOREMA 3.-
El ángulo formado por dos bisectrices
exteriores
de un triángulo es igual a noventa
grados, menos
la mitad del tercer ángulo.
δ = 90º - a
2

11. TEOREMA 4.-
El ángulo formado por una bisectriz
interior y
una bisectriz exterior de un triángulo es
igual a la
mitad del tercer ángulo.
δ = B^
2

12. VALOR DE LOS ÁNGULOS
EN LA CIRCUNFERENCIA

13. Sean los ángulos “α”:
ÁNGULO CENTRAL
α = AC

14. ÁNGULO INSCRITO
α = AC
2

15. Ángulo interior
α=AD-BC
2

16. Ángulo semi-inscrito
α = AB
2

17. Ángulo exincripto
α = ABD
2

18. Distancia de un punto a una
recta
“Es la longitud de la perpendicular trazada desde el
punto a la recta”.
AB: distancia de “A” a XX´

19. TRIÁNGULOS

20. LÍNEAS PRINCIPALES DEL
TRIÁNGULO
Son cuatro las líneas principales: Altura, Mediana,
Mediatriz y Bisectriz.

21. 1) ALTURA
Es la distancia de un vértice al lado opuesto o a
su
prolongación. Las ALTURAS se cortan en un
punto llamado ORTOCENTRO.

22. Si el triángulo es acutángulo, el
ortocentro es
Interior.

23. si es obtusángulo es exterior
ortocentro

24. Pero si es
rectángulo, es el punto de intersección de los
catetos.
ortocentro

25. TRIÁNGULO ÓRTICO O PEDAL
Es el triángulo cuyos vértices son los pies de las
alturas de un triángulo dado.
α , β y δ : ángulos del triángulo órtico.
“O” es el incentro del triángulo órtico.
Δ MNP: órtico o pedal.
Donde se cumple:
α = 180° - 2C
β = 180° - 2A
δ = 180° - 2B

26. 2)MEDIANA
Es el segmento que une un vértice con el punto
medio del lado opuesto.

27. Las MEDIANAS se intersectan en un punto llamado
BARICENTRO o CENTRO DE GRAVEDAD del
triángulo, este punto tiene la propiedad de dividir
a cada una de las medianas en la relación de dos es
a uno.
BARICENTRO

28. Por consiguiente, se cumple que:
OB 2 OD 1 BD
OD 1 OB 2 BD 3
3

29. TEOREMA.- En todo triángulo rectángulo, la mediana
relativa a la hipotenusa es igual a la mitad
de esa hipotenusa.
DB AC h
2 2
MEDIANA

30. 3) MEDIATRIZ
Es la perpendicular trazada desde el punto
medio
del lado de un triángulo. Las MEDIATRICES se
cortan en un punto llamado
CIRCUNCENTRO
por ser el centro de la circunferencia
circunscrita
al triángulo.
Cuando el triángulo es acutángulo, el
CIRCUNCENTRO
es interior, si es obtusángulo es exterior,
pero si es rectángulo, es el punto medio de
la
hipotenusa.

31. O: CIRCUNCENTRO

32. O:CIRCUNCENTRO

33. O:CIRCUNCENTRO

34. 4) BISECTRIZ
Es la recta que divide a un ángulo en dos ángulos
parciales iguales. Las BISECTRICES de un triángulo
se cortan en un punto “O” llamado INCENTRO
por ser el centro de la circunferencia inscrita
en el triángulo.
INCENTRO

35. EXCENTRO.- Es el punto “O” de intersección de
una bisectriz interior con dos bisectrices exteriores
relativas a los otros dos ángulos de un triángulo.
El excentro es el centro de la circunferencia exinscrita
al triángulo.
EXCENTRO

36. IGUALDAD DE TRIÁNGULOS
Para determinar la igualdad de dos triángulos,
bastará
establecer la igualdad de tres elementos, a
condición
de incluir en ellos, por lo menos un lado. Si esta
última cláusula no se cumple, se llegará sólo a la
semejanza de triángulos.
1er. Caso.- Dos triángulos son iguales cuando
tienen dos lados respectivamente iguales y el
ángulo comprendido entre éstos es igual.
2do. Caso.- Dos triángulos son iguales cuando
tienen un lado igual y los ángulos adyacentes a
estos, respectivamente iguales.
3er. Caso.- Dos triángulos son iguales cuando
tienen sus tres lados respectivamente iguales.

37. TEOREMAS DERIVADOS DE LA
IGUALDAD DE
TRIÁNGULOS
En virtud de la igualdad de
triángulos, se demuestra
los siguientes teoremas:

38. TEOREMA 1.-
Si por el punto medio del lado de un triángulo,
se
traza una paralela a otro lado, dicha paralela
pasará por el punto medio del tercer lado y su
longitud será igual a la mitad del lado al que es
paralelo.
Si M = punto medio de AB y
MN // AC ⇒ N = punto medio de BC

39. MN AC
2

40. TEOREMA 2.-
El “baricentro” o “Centro de Gravedad” de un
triángulo divide a cada una de las medianas en la
relación dos es a uno.
Δ ABC: OA OB OC 2
OF OD OE 1
C. G.

41. TEOREMA 3.-
En cualquier trapecio, la mediana es igual a la
semisuma de las bases; y el segmento que une los
puntos medios de las diagonales es igual a la
semidiferencia de las bases.
MN DC + AB EF DC -AB
2 2
M N

42. SEMEJANZA DE TRIÁNGULOS
Dos triángulos son semejantes
cuando tienen sus
ángulos respectivamente iguales, y
sus elementos
homólogos son proporcionales.
Se llama elementos homólogos a
aquellos que se oponen
a ángulos iguales, comparando
ambos triángulos.
Los casos generales de semejanza
de triángulos son:

43. 1er. Caso.- Cuando tienen sus 3 ángulos
iguales.
2do. Caso.- Cuando tienen un ángulo igual,
comprendido
entre lados proporcionales.
3er. Caso.- Cuando tienen sus lados
respectivamente
proporcionales.

44. TEOREMAS DERIVADOS DE LA SEMEJANZA DE
TRIÁNGULOS

45. TEOREMA DE THALES
Toda recta, paralela al lado de un triángulo y que
corta a los otros dos lados, determina un triángulo
parcial, semejante al total y recíprocamente.
Si: MN // AC
⇒ Δ ABC ∼ Δ MBN
Luego:
AB BC AC
BM BN MN

46. TEOREMA DE MENELAO
Toda recta que corta a los tres lados de un triángulo
determina en estos, seis segmentos; siendo el producto
de tres de ellos no consecutivos igual al producto
de los otros tres.
Δ ABC: AF . BE . CD = BF . CE . AD
FD: recta que corta a los tres lados.

47. TEOREMA DE CEVA
Las rectas que pasan por los vértices de un triángulo
y son concurrentes, determinan en los lados de éste,
seis segmentos; siendo el producto de tres de ellos no
consecutivos igual al producto de los otros tres.
Δ ABC: AD. BE . CF = BD . CE . AF

48. RELACIONES MÉTRICAS EN EL
TRIÁNGULO
RECTÁNGULO
En cualquier triángulo rectángulo,
se cumple las
siguientes propiedades:

49. 1° La altura relativa a la hipotenusa, es media
proporcional
entre los segmentos que determina
sobre ésta.
2° Cada cateto es media proporcional entre la
hipotenusa y su proyección sobre ésta.
3° La suma de los cuadrados de los catetos, es
igual
al cuadrado de la hipotenusa; es el teorema de
Pitágoras.
4° El producto de los catetos es igual al
producto de
la hipotenusa por la altura relativa a ésta.

50. 1° h² = mn
2° a² = bn
c² = bm
3° a² + c² = b²
4º ac = bh
m n

51. TEOREMA.-
En todo triángulo rectángulo, la inversa del
cuadrado de la altura relativa a la hipotenusa es
igual a la suma de las inversas de los cuadrados de
los catetos.
1 1 + 1
h² a² c²

52. RELACIONES MÉTRICAS EN EL
TRIÁNGULO
OBLICUÁNGULO

53. 1er caso.- En todo triángulo acutángulo, el cuadrado
del lado que se opone a un ángulo agudo es
igual a la suma de los cuadrados de los otros dos,
menos el doble producto de uno de éstos por la
proyección del otro sobre el que se ha tomado.
Δ ABC: a² = b² + c² - 2bp
Δ ABC: c² = a² + b² - 2bm

54. 2do. Caso.- En todo triángulo obtusángulo, el
cuadrado del lado que se opone al ángulo obtuso
es igual a la suma de los cuadrados de los otros
dos más el doble producto de unos de éstos por la
proyección del otro sobre el que se ha tomado.
Δ ABC: a² = b² + c² + 2bp