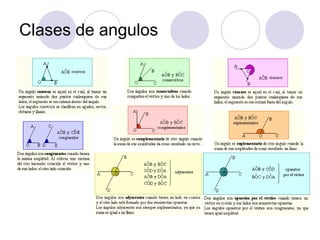
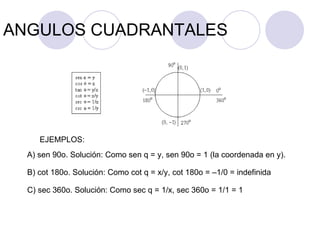
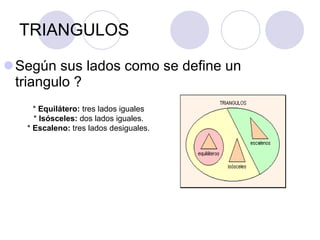
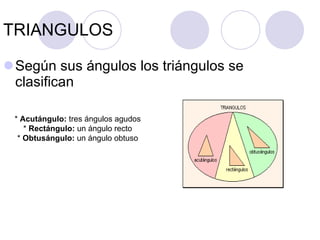
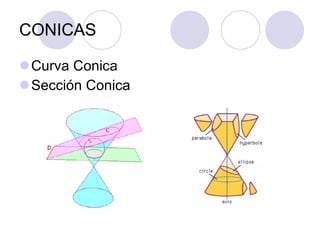
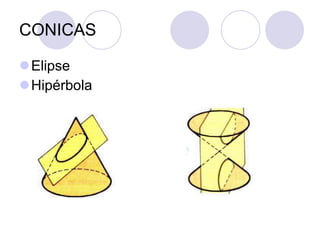
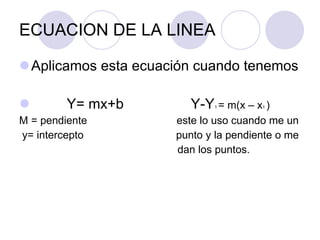
El documento proporciona una introducción a la trigonometría. Explica conceptos básicos como ángulos, funciones trigonométricas, identidades trigonométricas y su aplicación a triángulos. También cubre temas como el círculo trigonométrico, líneas y ángulos relacionados con círculos, y la representación analítica de figuras geométricas.

1. INSTITUCION EDUCATIVA RAFAEL NÚÑEZ SANDRA SALTARIN GOMEZ SINCELEJO- SUCRE 2010

2. Matemática: trigonometría Que es la trigonometría? trigonometría, rama de las matemáticas que estudia las relaciones entre los lados y los ángulos de triángulos, de las propiedades y aplicaciones de las funciones trigonometricas de ángulos. las dos ramas fundamentales son la trigonometría plana, que se ocupa de figuras contenidas en un plano, y la trigonometría esférica, que se ocupa de triángulos que forman parte de la superficie de una esfera.

3. Que es un Angulo? el Angulo es la porción de plano delimitada por dos semirrectas del mismo origen Los ángulos se identifican por 3 letras donde : La letra central corresponde al vértice Las otras 2 letras son puntos cualquiera de las semirrectas que lo forman

4. Angulos: se clasifican en Angulo recto : mide 90 grados Angulo agudo: mayor que 0 menor que 90 Angulo obtuso: mayor que 90 menor que 180 Angulo llano: mide 180 grados

5. Clases de angulos

6. Ángulos : complementarios y suplementarios son complementarios cuando la suma de sus valores es un ángulo recto , es decir, 90 grados sexagesimales . Dos ángulos son suplementarios cuando la suma de sus valores es igual a la de dos rectos, es decir(180º).

7. como saber si un ángulo es complementario o suplementario. Dos ángulos son complementarios si la suma de sus ángulos es igual a 90°. Si conocemos un ángulo, su ángulo complementario se puede encontrar restando la medida del mismo a 90o. Ejemplo: ¿Cuál es el ángulo complementario de 43o? Solución: 90° - 43° = 47° Dos ángulos son suplementarios si la suma de sus grados es igual a 180o. Si conocemos un ángulo, su ángulo suplementario se puede averiguar restando la medida del mismo a 180o. Ejemplo: ¿Cuál es el ángulo suplementario de 143o? Solución: 180° - 143° = 37°

8. ÁNGULOS Angulo coterminales- dos o mas ángulos que terminen en el mismo lugar.

9. ANGULOS CUADRANTALES EJEMPLOS: A) sen 90o. Solución: Como sen q = y, sen 90o = 1 (la coordenada en y). B) cot 180o. Solución: Como cot q = x/y, cot 180o = –1/0 = indefinida C) sec 360o. Solución: Como sec q = 1/x, sec 360o = 1/1 = 1

10. FUNCIONES TRIGONOMETRICAS Seno = Opuesto/Hipotenusa Cosecante = Hipotenusa/Opuesto Coseno = Adyacente/Hipotenusa Secante = Hipotenusa/Adyacente Tangente = Opuesto/Adyacente Cotangente = Opuesto/Adyacente

11. FUNCIONES TRIGONOMETRICAS Trucos para memorizar fácilmente las 6 funciones trigonometricas: SOHCAHTOA: Seno = opuesto/Hipotenusa Coseno = Adyacente/Hipotenusa Tangente = Opuesto/Adyacente CHOSHACAO: Cosecante = Hipotenusa/Opuesto Secante = Hipotenusa/Adyacente Cotangente = Adyacente/Opuesto

12. IDENTIDADES: En matemática , las identidades trigonométricas son igualdades que involucran funciones trigonométricas , verificables para cualquier valor de las variables que se consideren (es decir para cualquier valor que pudieran tomar los ángulos sobre los que se aplican las funciones).

13. IDENTIDADES Sec A = 1/Cos A ;Cos A Sec A = 1 Csc = 1/SenA ; Sen A Csc A = 1 Tan A = Sen A/Cos A Tan A Cot A = 1 Cot A = Cos A/Sen A Sen ²A+Cos²A = 1 Sen²A=1-Cos²A Cos²A=1-Sen²A Tan²A+1=Sec²A Tan²A=Sec²A-1 1=Sec²A-Tan²A Cot²A+1=Csc²A Cot²A=Csc²A-1 1=Csc²A-Cot²A

14. ANGULOS Ángulos Dobles sen2A=2senA cos A cos2A=cos ²A-Sen²A tan2A=2TanA/1-Tan²A=Sen2A/Cos2A Csc2A=1/Sen2A Sec2A=1/CoS2A Cot2A=Cos2A/Sen2A

15. IDENTIDADES Ángulos Medios sen1/2 A= √1- cosA/2 Csc1/2 A= √ 1+cosA/2 Tan1/2 A = √ 1-cosA/1+cosA=Sen 2A/cos 2ª Csc1/2 A = √ 1/sen2 A Sec ½ A = √ 1 /cos2 A Cot ½ A = √ cos2 A/sen2 A

16. IDENTIDADES Suma y/o Resta De Ángulos sen(A ±B) =sen A cos B ± Sen B Cos A Csc(A ±B) = 1/sen (A+B) Cos(A+B) = cosA cosB ±senA senB Sec(A ±B) = 1/cos (A ±B) Tan(A ±B) = TanA ±TanB/1 ±TanA TanB Cot(A ±B) = Cos(A ±B)/Sen(A ±B)

17. IDENTIDADES Ángulos Dobles Sen2 ∞= 2Sen∞Cos∞ Csc2 ∞ = 1 Cos2 ∞=cos ² ∞ -Sen² ∞ sen2 ∞ Tan2 ∞ = 2tan ∞ = Sen2 ∞ Sec2 ∞= 1 1-tan² ∞ cos2∞ Cos2 ∞ Cot 2 ∞= Cos2 ∞ = 1 Sen2 ∞ Tan2 ∞

18. IDENTIDADES Ángulos medios Sen1/2 ∞= √ 1-Cos∞ Csc1/2= 1 2 Sen1/2 ∞ Cos1/2∞= √ 1+Cos ∞ Sec1/2 ∞ = 1 Tan1/2 = √ 1-Cos ∞= Sen1/2 ∞ Cos1/2 ∞ 1+Cos∞ Cos1/2∞ Cot1/2∞= Cos1/2∞ Sen1/2∞

19. IDENTIDADES Ejemplos : Cot 120° (usando ángulos dobles y ángulos especiales). Cot2(60°) = Cos 2(60) = Cos ²60-sen²60 Sen 2(60) 2Sen60Cos60 = (1/2) ² - (3/2) 2( 3/2) (1/2) = 1/4 – 3/4 2√ 3/4 = -2/4 = 2 * √3 * √3 2 3 √ 4 2 √ 3 √3 √3

20. Ley del Seno En todo triángulo se da la siguiente relación entre la longitud de sus lados A, B y C y el seno de sus respectivos ángulos opuestos a, b y c a/sin A = b/Sin B = c/Sin C

21. Ley del Coseno En todo triángulo «El cuadrado de un lado es igual a la suma de los cuadrados de los otros lados menos el doble del producto de estos lados por el coseno del ángulo comprendido...»

22. TRIANGULOS ESPECIALES

23. TRIANGULOS ESPECIALES Se usa esta ecuación para graficar. y = ±C ±A sen o cos B(∞±D) C= desplazamiento A= amplitud B=numero de ciclos D=desplazamiento horizontal

24. TRIANGULOS ESPECIALES Ejemplos: Función Seno

25. TRIANGULOS ESPECIALES Ejemplos: Función Coseno

26. TRIANGULOS ESPECIALES Ejemplos: Función Tangente

27. TRIANGULOS ESPECIALES Ejemplos : Función Secante

28. TRIANGULOS ESPECIALES Ejemplos : Función cosecante

29. TRIANGULOS ESPECIALES Ejemplos : Función Cotangente

30. TRIANGULOS Que es un triángulos ? Porción de plano limitada por 3 líneas que se cortan de dos en dos, en un punto común llamado vértice, tiene 3 vértices y 3 lados.

31. TRIANGULOS Según sus lados como se define un triangulo ? * Equilátero: tres lados iguales * Isósceles: dos lados iguales. * Escaleno: tres lados desiguales.

32. TRIANGULOS Según sus ángulos los triángulos se clasifican * Acutángulo: tres ángulos agudos * Rectángulo: un ángulo recto * Obtusángulo: un ángulo obtuso

33. TRIANGULOS El área de un triangulo siempre se coloca en unidades cuadradas El Área de un triangulo es = Base * altura sobre 2 Subperimetro: el perímetro dividido entre 2 El perímetro se saca sumando todos los lados del triangulo. Cateto al cuadrado+cateto al cuadrado=hipotenusa al cuadrado Otra forma de sacar el Área de un triangulo es A=√S(s-L 1 )(S-L 2 )(S-L 3 )

34. TRIANGULOS Ortocentro : Se denomina ortocentro al punto donde se cortan las tres alturas del triangulo.

35. TRIANGULOS Incentro : es el punto de corte de las bisectrices interiores de un triangulo

36. GEOMETRIA: ANALITICA Que es la geometría Analítica y para que nos sirve ? se conoce como geometría analítica al estudio de ciertos objetos geométricos mediante técnicas básicas del Análisis matemático y del Algebra. lo novedoso de la geometría analítica es que permite representar figuras geométricas mediante formulas del tipo f(x,y)=0 donde f representa una función .

37. CIRCULO Centro (0 ,0) X ² + Y² =r² Centro (h , k) (x-h) ² +(y-k) ²= r² Diámetro = 2 veces el radio

38. CIRCULO Distancia entre 2 puntos : D= √ ( x 2 -x 1 ) ² +(y 2 -y 1 ) ² Distancia de un punto a una línea : D= / Ax+By+C / √ A ²+B²

39. CIRCULO Punto Medio : Pm: (xm= x 1 +x 2 /2) (ym= x 1 +x 2 /2) Área del Circulo : π r ² Formula General : X ²+y²+Bx+Cy+D=0 Circunferencia o perímetro : 2 π r

40. CIRCULO Cuando: El radio al cuadrado es mayor que 0,es Circulo real. El radio al cuadrado es igual que 0, es Punto. El radio al cuadrado es menor que 0 , es Circulo Imaginario.

41. CIRCULO Área sector : π r ²n / 360 Área Segmento : A Sector - A Δ Longitud del sector 2 π rn/360 Área Corona Circular π r ² = π R ² Β = π (R ² - r²)

42. ANGULOS Y LINEAS A UN CIRCULO Líneas tangentes trazadas desde un punto exterior con iguales, tienen la misma medida ∞ = arco mayor – arco menor 2 L1=L2

43. ANGULOS Y LINEAS A UN CIRCULO Líneas secantes : Trazados desde un punto exterior Secante* Seg.Ext = Secante* Seg.Ext B = arco - arco 2

44. ANGULOS Y LINEAS A UN CIRCULO Línea tangente y secante : Trazados desde un punto exterior Tan ² = Secante* Seg.Ext

45. ANGULOS Y LINEAS A UN CIRCULO Cuerdas que se cortan dentro de un circulo

46. ANGULOS ∞ = Angulo centra β = Angulo inscrito Angulo central = Arco Angulo inscrito=1/2 Arco

47. ANGULOS Punto a una razón dada = (xr = x 1 +r(x 2 -x 1 ) (yr = y 1 +r(y 2 -y 1 ) Area del triangulo: A Δ = B*h /2 A = √ S(s-a)(s-b)(s-c) S=a+b+c / 2 A Δ equilatero = l ² √3 / 4

48. ANGULOS Dados 2 puntos. Se busca la pendiente 1) M = y 2 –y 1 x 2 - x 1 2) y – y 1 =m(x – x 1 ) 3) (x 1 ,y 1 )(x 2 ,y 2 ) Dado un punto y la pendiente 1) Encuentras M 2) P(x 1 ,y 1 ) 3) y – y 1 =m(x – x 1 )

49. ANGULOS Dada la pendiente (m) y el intercepto con el eje y (b) y=mx+b Dado los 2 intercepto (a,b) x/a+y/b=1 Forma general: Ax+By+C = 0 Para dar la inclinación de la línea Pendiente = tan β

50. ANGULOS Ecuación de la mediatriz: Mediatriz: es la linea que sale del punto medio de un segmento en forma perpendicular. Hallo punto medio del segmento Hallo pendiente de ese segmento y la paso a perpendicular Hago la ecuación: y-y 1 = m(x-x 1 )

51. ANGULOS Ecuación de la Altura : Hallo pendiente del segmento donde llega y la paso a perpendicular Hago la ecuación con M y el punto donde sale la altura : y-y 1 =m(x-x 1 )

52. ANGULOS Ecuación de la mediana : Mediana: es el segmento que tiene por extremos, un vértice y el punto medio del lado opuesto. 1) Hallo punto medio del segmento donde 2) Busco pendiente del punto medio, y punto de donde sale 3) Escribo la ecuación (y-y 1 )=m(x-x 1 )

53. ANGULOS Líneas paralelas tienen pendientes iguales Líneas perpendiculares: inversas y signo contrario m= -1/m Línea paralela al eje x tiene m = 0 Línea paralela al eje y tiene m = 1/0

54. CONICAS Elipse a=punto final eje mayor sus coordenadas se llaman vértice b=punto final eje menor, sus coordenadas se nombran B c= foco c ² = a ² – b ² Lr= lado recto lr=2b ² /a E=exentridad e= c/a e <1 e = c/a Horizontal Vertical x ² + y ² = 1 x ² + y ² =1 a ² b ² a ² b ²

55. CONICAS a=punto final eje mayor , sus coordenadas se llaman vertical b=punto final eje menor, sus coordenadas se nombran B c= foco c ² = a ² - b ² Lr= lado recto lr= 2b ² /a Excentridad e=c/a debe ser menor que 1 a= punto final eje real o transversal, sus coordenadas se llaman vértice b= punto final eje conjugado o imaginario, sus coordenadas se llaman B C= foco c ² =a ² + b ² Lr= lado recto lr= 2b ² /a E=c/a debe ser mayor que 1

56. CONICAS Elipse E Hipérbola Elipse E Hipérbola Horizontal Vertical C (0,0) C (0,0) v ( ±a,0) v (0, ±a) (0, ±b) β ( ±b,0) f (±c,0) f (0, ±c) Pf (±c, ±1/2L) pf (±1/2Lr ±c) Siempre c < a Siempre c > a

57. CONICAS Eje mayor o eje real o transversal= 2a Eje menor o eje conjugado o imaginario = 2b Elipse hipérbola

58. CONICAS Distancia focal 2c El centro es el punto medio entre los dos vértices (v), los dos puntos finales del eje menor o conjugado (B) o los dos focos (F).el foco es el punto medio entre los dos puntos finales.

59. CONICAS ELIPSE C (h,k) HIPERBOLA Horizontal Horizontal (x – h) ² + (y – k) ² = 1 (x – h) ² - (y – k) = 1 a ² b ² a ² b ² Vertical Vertical (x – h) ² + (y – k) ² = 1 ( y – k) ² - (x – h) ² b ² a ² a ² b ²

60. CONICAS Elipse - Hipérbola Elipse – Hipérbola C (h,k) Horizontal C (h,k) Vertical v (h ±a,k) v (h,k±a) (h,k ±b) β (h ±b,k) f (h±c,k) f (h,k±c) pf (h ±c,k1/2L r ) pf (h ±1/2L r ,k± c)

61. CONICAS Parabola e = 1 v (0,0) v (h,k) y ²= 4ax (y – k ) ² =4ª(x – h) Lr = 4ª Lr= 4a f (a,0) f ( h +a, k) D: x= -a D: x= h – a pf ( a, ±2ª) pf (h+a,k ±2a) vf = vd Distancia del vertice al foco = Distancia de vertice a directriz

62. CONICAS Vértice es el punto medio entre foco y directriz. Foco es el punto medio entre los 2 puntos finales. y ² = -4ac (y – k)²= -4ac (x – h) f (- a,0) f (h-a, k) D: x =a D: x= h +a pf (-a,±2ª) pf (h-a,k±2ª)

63. CONICAS x ²=4ay (x-h)²= (y-k) f (0,a) f(h,k+a) D: y=-a D: y= k -a pf=(±2a,a) pf(h±2a,k+a)

64. CONICAS x ²= -4ay (x-h)²= -4 a (y-k) f (0,-a) f(h,k-a) D: y=a D: y= k +a pf=(±2a,-a) pf(h±2a,k-a)

65. CONICAS Curva Conica Sección Conica

66. CONICAS Elipse Hipérbola

67. ECUACION DE LA LINEA cuando te dan dos puntos. Se usa esta formula: M = y2 - y1/ x2 - x1 cuando te dan la ecuación Ax + By + C = 0. se usa esta formula : M = -a/ b

68. ECUACION DE LA LINEA Aplicamos esta ecuación cuando tenemos Y= mx+b Y-Y 1 = m(x – x 1 ) M = pendiente este lo uso cuando me un y= intercepto punto y la pendiente o me dan los puntos.

69. ECUACION DE LA LINEA Cuando nos dan los intercepto y la formula general. Ax + By + C = 0 x + y = 1 Formula general de a b de una linea

70. GENERALIDADES Para hallar el intercepto en y: Igualo x = 0 y busco y para hallar el intercepto en x : igualo y = 0 y busco x

71. GENERALIDADES Para hallar la pendiente y la inclinación aplicamos la siguiente ecuación : m = y 2 -y 1 / x 2 -x 1 y con la respuesta pongo en la calculadora shift tan de la respuesta: Tan B =m

72. GENERALIDADES Para hallar la simetría: X = -x misma ecuación simétrica eje y Y = -y misma ecuación simétrica eje x Para hallar simetría en el origen: X=-x, y=-y misma ecuación simétrica origen

73. GENERALIDADES Cuando me dan la ecuación de una línea Ax+By+C = 0 m = -A / B

74. GENERALIDADES Punto a una razon dada : Xr = X 1 + r (x 1 – x ) Yr = Y 1 + r (y 1 – y )

75. GENERALIDADES Para hallar el punto medio : Xm = x 1 + x 2 / 2 Ym = y 1 + y 2 / 2

76. GENERALIDADES Dominio : también llamado -Codominio -Recorrido -Conjunto de llegada -Imagen

77. GENERALIDADES Rango : también nombrado -PRE imagen -conjunto de partida

78. GENERALIDADES Dominio : se despeja Y para hallar X En la respuesta se coloca D: XER/X ≠ de la respuesta

79. GENERALIDADES Rango : se despeja x para hallar Y En la respuesta se coloca D: YER/Y ≠ de la respuesta

80. PARABOLA Una parábola es el conjunto de puntos del plano cuya distancia a una recta fija es igual a la distancia hasta un punto fijo. La recta fija se llama directriz de la parábola y el punto fijo se llama foco