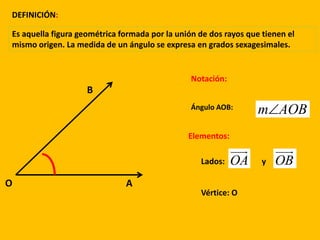
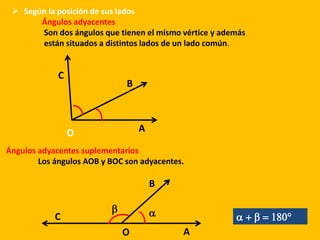
Este documento define los ángulos geométricos y clasifica sus tipos. Explica que un ángulo está formado por dos rayos que comparten un vértice y se miden en grados. Los clasifica como agudos, rectos, obtusos o llano según su medida, y como adyacentes, consecutivos u opuestos según la posición de sus lados. Además, resuelve 7 ejercicios de ángulos que implican sumas, relaciones y bisectrices.

2. DEFINICIÓN:
Es aquella figura geométrica formada por la unión de dos rayos que tienen el
mismo origen. La medida de un ángulo se expresa en grados sexagesimales.
O A
B
Notación:
Ángulo AOB:
m AOB
Elementos:
Lados: OA OBy
Vértice: O

3. CLASIFICACIÓN DE ÁNGULOS:
 Según su medida:
Ángulo agudo
Cuando su medida es mayor que 0° y menor que
90°.
a 0 < a < 90
Ángulo recto
Cuando su medida es igual a 90°.

4. Ángulo obtuso
Cuando su medida es mayor que 90° y menor que 180°.
a
90<a < 180
Ángulo llano
Cuando su medida es igual a 180°.
a
a = 180

5.  Según la posición de sus lados
Ángulos adyacentes
Son dos ángulos que tienen el mismo vértice y además
están situados a distintos lados de un lado común.
O A
B
C
Ángulos adyacentes suplementarios
Los ángulos AOB y BOC son adyacentes.
O A
B
C ab
a + b = 180

6. O A
B
CDD
a
bq
m
Ángulos consecutivos en un mismo semiplano
Los ángulos AOB, BOC, COD y DOE son consecutivos.
O B
C
D
E
F
a
bq
m
a + b + q + m = 180°

7. Ángulos coplanares alrededor del vértice
a° + q  b° + ° + ° = 360°
a
q

b
A
B
C
D
O

8. Ángulos opuestos por el vértice
ab a = b
Bisectriz de un ángulo.
O
A
B
C
a
a

9. Ejercicios resueltos.
1. Se tiene os ángulos consecutivos : AOB; BOC Y COD tal que
2 , 5m AOB x m BOC x =  = y 3m COD x =
Hallar la medida de los ángulos BOC, si el ángulo AOD es llano
Desarrollo:
O A
B
C
D
2x
5x
3x
3x + 5x + 2x = 180°
X = 18° El ángulo BOC = 90°

10. 2. Se tiene dos ángulos complementarios tal que uno es los 4/5
del otro. ¿ Cuánto mide el mayor de ellos?
Desarrollo:
x
4
5
x
4/5 x + x = 90°
x = 50°

11. 3.Dos ángulos adyacentes suplentarios difieren en 40°. Hallar la medida del
mayor ángulo.
4. ¿Cuánto mide un ángulo, si la diferencia entre su suplemento y su complemento
es 6 veces el ángulo?
Desarrollo:
aa + 40°
a + 40° + a = 180°
a = 70° Entonces la medida del ángulo mayor es : 110°
Desarrollo:
Sea «a» el ángulo.

12. El suplemento será: 180° - a
El complemento será: 90° - a
( 180° - a ) – ( 90° - a ) = 6a
180° - a – 90° + a = 6a
a = 15°
5. Tres ángulos consecutivos suma 130°; el ángulo intermedio mide
20°. Halla la medida del ángulo formado por las bisectrices del
primero y el tercer ángulo.
Desarrollo:

13. 20° a
a
bb
2b + 2 a + 20° = 130°
a + b = 55°
El ángulo pedido será: 75°

14. 6.Se tienen los ángulos consecutivos AOB y BOC, tal que el ángulo AOC es recto
Halla la medida del ángulo AOB, si dichos ángulos AOB y BOC están en relación
de 4 a 5.
Desarrollo:
O A
B
C
a
b
4
5
K
a
b
= =
4
5
K
K
a
b
=
=
4K + 5K = 90°
K = 10°
40m AOB = 

15. 7. Se tiene los ángulos adyacentes AOB y BOC de manera que:
80m AOB m AOC +  =  Halla m AOM , siendo
bisectriz del ángulo BOC
Desarrollo:
O A
C
B
OM
M
a a
80m AOB m AOC +  = 
x
X + x + 2 a = 80°
2x + 2a = 80°
40m AOM = 