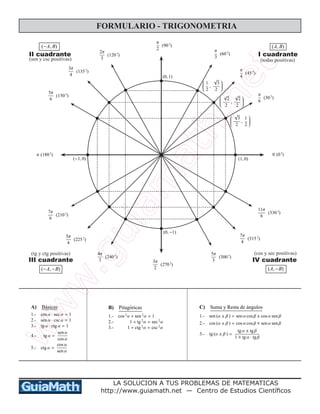
Este documento presenta varias fórmulas y conceptos clave de trigonometría, incluyendo: 1) relaciones básicas entre funciones trigonométricas; 2) identidades trigonométricas; 3) sumas y diferencias de ángulos; 4) ángulos dobles y medios; 5) teoremas del seno y coseno; y 6) relaciones en triángulos rectángulos. El documento provee una guía completa de los principios fundamentales de trigonometría.

1. w
w
w.guiam
ath.net
FORMULARIO - TRIGONOMETRIA


√
3
2
,
1
2




√
2
2
,
√
2
2




1
2
,
√
3
2


(1, 0)
(0, 1)
(−1, 0)
(0, −1)
π
2
(90
o
.)
2π
3
(120
o
.)
π
4
(45
o
.)
π
6
(30
o
.)
π
3
(60
o
.)
3π
4
(135
o
.)
5π
6
(150
o
.)
π (180
o
.)
7π
6
(210
o
.)
5π
4
(225
o
.)
4π
3
(240
o
.)
3π
2
(270
o
.)
5π
3
(300
o
.)
7π
4
(315
o
.)
11π
6
(330
o
.)
0 (0
o
.)
(A, B)(−A, B)
(−A, −B) (A, −B)
II cuadrante
III cuadrante IV cuadrante
I cuadrante
(sen y csc positivas) (todas positivas)
(cos y sec positivas)(tg y ctg positivas)
A) B´asicas
1.- cos α · sec α = 1
2.- sen α · csc α = 1
3.- tg α · ctg α = 1
4.- tg α =
sen α
cos α
5.- ctg α =
cos α
sen α
B) Pitag´oricas
1.- cos 2
α + sen 2
α = 1
2.- 1 + tg 2
α = sec 2
α
3.- 1 + ctg 2
α = csc 2
α
LA SOLUCION A TUS PROBLEMAS DE MATEMATICAS
http://www.guiamath.net — Centro de Estudios Científicos
C) Suma y Resta de ´angulos
1.- sen (α ± β ) = sen α cos β ± cos α sen β
2.- cos (α ± β ) = cos α cos β ∓ sen α sen β
3.- tg (α ± β ) =
tg α ± tg β
1 ∓ tg α · tg β
D) Angulos dobles
1.- sen 2α = 2 sen α cos α
2.- cos 2α = cos 2
α − sen 2
α
= 2 cos 2
α − 1
= 1 − 2 sen 2
α
3.- tg 2α =
2 tg α
1 − tg 2α
A) B´asicas
1.- cos α · sec α = 1
2.- sen α · csc α = 1
3.- tg α · ctg α = 1
4.- tg α =
sen α
cos α
5.- ctg α =
cos α
sen α
B) Pitag´oricas
1.- cos 2
α + sen 2
α = 1
2.- 1 + tg 2
α = sec 2
α
3.- 1 + ctg 2
α = csc 2
α

2. w
w
w.guiam
ath.net
4.- sen α =
1 − cos 2α
2
5.- cos α =
1 + cos 2α
2
E) Angulos medios
1.- sen α = 2 sen (α/2) cos (α/2)
2.- cos α = cos 2
(α/2) − sen 2
(α/2)
3.- sen 2
(α/2) =
1 − cos α
2
4.- cos 2
(α/2) =
1 + cos α
2
5.- tg (α/2) =
sen α
1 + cos α
=
1 − cos α
sen α
2.- cos (α ± β ) = cos α cos β ∓ sen α sen β
3.- tg (α ± β ) =
tg α ± tg β
1 ∓ tg α · tg β
D) Angulos dobles
1.- sen 2α = 2 sen α cos α
2.- cos 2α = cos 2
α − sen 2
α
= 2 cos 2
α − 1
= 1 − 2 sen 2
α
3.- tg 2α =
2 tg α
1 − tg 2α
4.- sen α =
1 − cos 2α
2
5.- cos α =
1 + cos 2α
2
E) Angulos medios
1.- sen α = 2 sen (α/2) cos (α/2)
2.- cos α = cos 2
(α/2) − sen 2
(α/2)
3.- sen 2
(α/2) =
1 − cos α
2
4.- cos 2
(α/2) =
1 + cos α
2
5.- tg (α/2) =
sen α
1 + cos α
=
1 − cos α
sen α
F) de Producto a Suma
1.- sen A · cos B =
1
2
[sen (A + B) + sen (A − B)]
2.- cos A · cos B =
1
2
[cos (A + B) + cos (A − B)]
3.- sen A · sen B = −
1
2
[cos (A + B) − cos (A − B)]
G) de Suma a Producto
1.- sen X + sen Y = 2 sen
 X + Y
2

· cos
 X − Y
2

2.- sen X − sen Y = 2 sen
 X − Y
2

· cos
 X + Y
2

3.- cos X + cos Y = 2 cos
 X + Y
2

· cos
 X − Y
2

4.- cos X − cos Y = −2 sen
 X + Y
2

· sen
 X − Y
2

LA SOLUCION A TUS PROBLEMAS DE MATEMATICAS
http://www.guiamath.net — Centro de Estudios Científicos
F) de Producto a Suma
1.- sen A · cos B =
1
2
[sen (A + B) + sen (A − B)]
2.- cos A · cos B =
1
2
[cos (A + B) + cos (A − B)]
3.- sen A · sen B = −
1
2
[cos (A + B) − cos (A − B)]
G) de Suma a Producto
1.- sen X + sen Y = 2 sen
 X + Y
2

· cos
 X − Y
2

2.- sen X − sen Y = 2 sen
 X − Y
2

· cos
 X + Y
2

3.- cos X + cos Y = 2 cos
 X + Y
2

· cos
 X − Y
2

4.- cos X − cos Y = −2 sen
 X + Y
2

· sen
 X − Y
2

H) Periodicidad
Si k ∈ ZZ ,
1.- sen (α ± 2kπ) = sen α
2.- cos (α ± 2kπ) = cos α
3.- tg (α ± kπ) = tg α
4.- ctg (α ± kπ) = ctg α
5.- sec (α ± 2kπ) = sec α
6.- csc (α ± 2kπ) = csc α
I) Formulas de Reducci´on (Ley del Burro)
Sea f cualesquiera de las funciones trigonom´etricas y cf su
co-funci´on. Si s denota el signo que tiene la funci´on f en el
cuadrante correspondiente, se cumple que:
1.- f

π
2π
± θ

= s f(θ) 24 f´ormulas.
2.- f

π/2
3π/2
± θ

= s cf(θ) 24 f´ormulas.
J) Teorema del Seno
En cualquier tri´angulo, si L1 representa la medida del lado op-
uesto al ´angulo 1 y L2 es la medida de cualquier otro lado op-
uesto de un cierto ´angulo 2, siempre se cumple que:
sen (1)
L1
=
sen (2)
L2
Esto quiere decir que en el siguiente tri´angulo, se cumplen las
f´ormulas:
1.-
sen α
a
=
sen β
b
2.-
sen β
b
=
sen γ
c
3.-
sen α
a
=
sen γ
c
K) Teorema del Coseno
Si L1 , L2 y L3 representan las medidas de cada uno de los lados de un
tri´angulo cualquiera, y si 1 es la medida del ´angulo opuesto al lado L1,
siempre se cumple que:
L2
1 = L2
2 + L2
3 − 2 L2 L3 cos (1)
Es decir, en el siguiente tri´angulo se cumplen las f´ormulas:
A B
C
ab
c
1.- a2
= b2
+ c2
− 2 b c cos α
2.- b2
= a2
+ c2
− 2 a c cos β
3.- c2
= a2
+ b2
− 2 a b cos γ
B
C A
a
c
b
α
β
γ
α
β
γ
α
β
γ
α
β
γ
α
β
γ
α
β
γ
L) Relaciones en el Tri´angulo Rect´angulo
En todo tri´angulo rect´angulo, siempre se cumple que:
1.- sen α =
cateto opuesto
hipotenusa
=
CO
HIP
2.- cos α =
cateto adyacente
hipotenusa
=
CA
HIP
3.- tg α =
cateto opuesto
cateto adyacente
=
CO
CA
4.- ctg α =
cateto adyacente
cateto opuesto
=
CA
CO
5.- sec α =
hipotenusa
cateto adyacente
=
HIP
CA
6.- csc α =
hipotenusa
cateto opuesto
=
HIP
CO
L) Relaciones en el Tri´angulo Rect´angulo
En todo tri´angulo rect´angulo, siempre se cumple que:
1.- sen α =
cateto opuesto
hipotenusa
=
CO
HIP
2.- cos α =
cateto adyacente
hipotenusa
=
CA
HIP
3.- tg α =
cateto opuesto
cateto adyacente
=
CO
CA
4.- ctg α =
cateto adyacente
cateto opuesto
=
CA
CO
5.- sec α =
hipotenusa
cateto adyacente
=
HIP
CA
6.- csc α =
hipotenusa
cateto opuesto
=
HIP
CO
A
C
B
α
β
γ
CA
CO
HIP
*recordar el: cocacoca-hiphip
CO
HIP
CA
HIP
CO
CA
CA
CO
HIP
CA
HIP
CO
J) Teorema del Seno
En cualquier tri´angulo, si L1 representa la medida del lado opuesto
al ´angulo 1 y L2 es la medida de cualquier otro lado opuesto de un
cierto ´angulo 2 , siempre se cumple que:
sen cos tg ctg sec cscsen cos tg ctg sec cscsen cos tg ctg sec csc
A) B´asicas
1.- cos α · sec α = 1
2.- sen α · csc α = 1
3.- tg α · ctg α = 1
4.- tg α =
sen α
cos α
5.- ctg α =
cos α
sen α
B) Pitag´oricas
1.- cos 2
α + sen 2
α = 1
2.- 1 + tg 2
α = sec 2
α
3.- 1 + ctg 2
α = csc 2
α
A) B´asicas
1.- cos α · sec α = 1
2.- sen α · csc α = 1
3.- tg α · ctg α = 1
4.- tg α =
sen α
cos α
5.- ctg α =
cos α
sen α
B) Pitag´oricas
1.- cos 2
α + sen 2
α = 1
2.- 1 + tg 2
α = sec 2
α
3.- 1 + ctg 2
α = csc 2
α