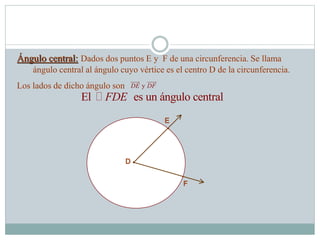
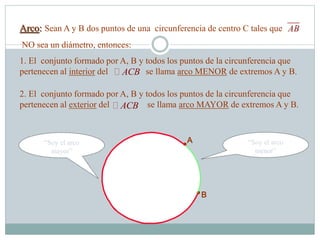
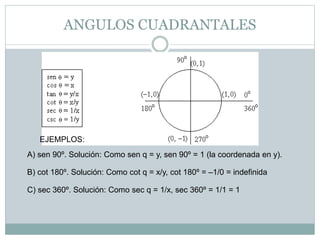
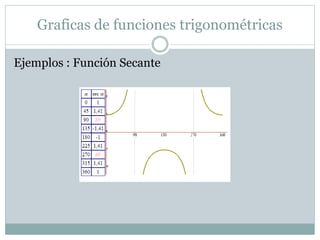
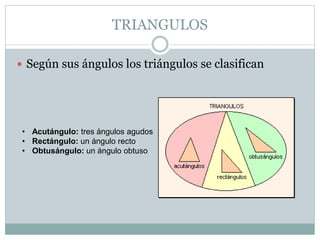
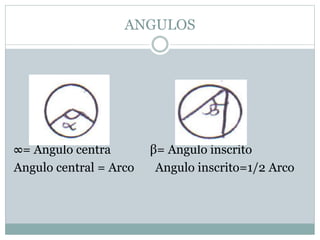
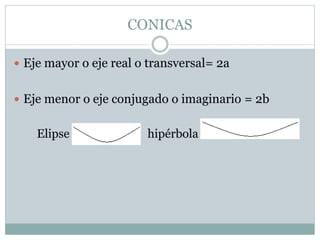
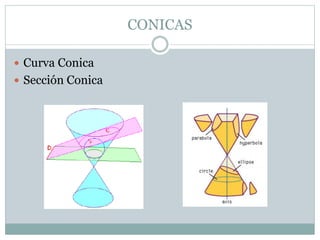
Este documento presenta los objetivos y conceptos básicos sobre círculos y circunferencias. Los objetivos incluyen diferenciar círculos y circunferencias, reconocer líneas y ángulos del círculo, y aplicar teoremas a problemas. Define conceptos como circunferencia, radio, cuerda, diámetro, interior y exterior del círculo. Explica definiciones de ángulo central, arco, semicircunferencia y notaciones. Finalmente, presenta seis teoremas importantes sobre líneas en la circunferencia
Las capacidades sociomotrices son las que hacen posible que el individuo se pueda desenvolver socialmente de acuerdo a la actuación motriz propias de cada edad evolutiva del individuo; Martha Castañer las clasifica en: Interacción y comunicación, introyección, emoción y expresión, creatividad e imaginación.
ACERTIJO DE CARRERA OLÍMPICA DE SUMA DE LABERINTOS. Por JAVIER SOLIS NOYOLAJAVIER SOLIS NOYOLA
El Mtro. JAVIER SOLIS NOYOLA, crea y desarrolla ACERTIJO: «CARRERA OLÍMPICA DE SUMA DE LABERINTOS». Esta actividad de aprendizaje lúdico que implica de cálculo aritmético y motricidad fina, promueve los pensamientos lógico y creativo; ya que contempla procesos mentales de: PERCEPCIÓN, ATENCIÓN, MEMORIA, IMAGINACIÓN, PERSPICACIA, LÓGICA LINGUISTICA, VISO-ESPACIAL, INFERENCIA, ETCÉTERA. Didácticamente, es una actividad de aprendizaje transversal que integra áreas de: Matemáticas, Neurociencias, Arte, Lenguaje y comunicación, etcétera.
2. OBJETIVOS
Diferenciar los conceptos de círculo y circunferencia.
Reconocer y graficar las lineas y ángulos del círculo.
Aplicar los teoremas de lineas y ángulos a la solución
de ejercicios y problemas.
Escribir la ecuación del círculo con C(0,0) y C(h,k)
según la información dada.
Analizar la ecuación de un círculo encontrando
centro y radio y clasificando si es punto, círculo real
ó imaginario.
4. Definiciones Básicas
Radio:
segmento cuyos extremos son el centro de la circunferencia y otro punto
de la misma. También se le llama radio a la medida de esos segmentos.
.O
P.
r
r
5. Definiciones Básicas
Cuerda: Segmento cuyos extremos son DOS puntos de la circunferencia.
Diámetro: Cuerda que contiene al centro de la circunferencia.
.O
P
M
C
N
A
G
Cuerdas: , ,PM NC GA
Diámetro: NCr
r
6. Interior de la circunferencia: Conjunto de puntos coplanares a la
circunferencia, que están a una distancia del centro MENOR que el radio.
Exterior de la circunferencia: Conjunto de puntos coplanares a la
circunferencia, que están a una distancia del centro MAYOR que el radio.
O
. P
, , , , están en el Exterior de la circunferenciaP F L M K
. M
. L
. F
. K
r
PO r
FO r
LO r
MO r
KO r
, , están en el Interior de la circunferenciaJ G W
. G
. W
. J
JO r
GO r
WO r
7. Definiciones Básicas
Círculo:
Unión de la circunferencia y su interior. Conjunto de puntos
coplanares que están a una distancia menor o igual que el radio.
.O
P.
Círculo de centro y radioP OP
8. Ángulo central: Dados dos puntos E y F de una circunferencia. Se llama
ángulo central al ángulo cuyo vértice es el centro D de la circunferencia.
Los lados de dicho ángulo son yDE DF
.
.
E
F
D
El es un ángulo centralFDE
9. Arco: Sean A y B dos puntos de una circunferencia de centro C tales que
NO sea un diámetro, entonces:
1. El conjunto formado por A, B y todos los puntos de la circunferencia que
pertenecen al interior del se llama arco MENOR de extremos A y B.
2. El conjunto formado por A, B y todos los puntos de la circunferencia que
pertenecen al exterior del se llama arco MAYOR de extremos A y B.
AB
ACB
ACB
A.
B.
“Soy el arco
menor”
“Soy el arco
mayor”
10. Notaciones:
Si un arco tiene extremos A y B lo denotamos:
Como suele haber ambigüedad escribimos donde M es
un punto cualquiera del arco.
Por costumbre se suele utilizar para el arco menor.
AB
AMB
AB
A
B.
.
M
N
.
Arco Menor:
Arco Mayor:
Arco Menor:
AMB
ANB
AB
11. 3. Si en las definiciones anteriores es un diámetro, en lugar de “arco”
llamamos a esa parte SEMICIRCUNFERENCIA
AB
A O. B
“Soy una
semicircunferencia
12. A
.
B.
Rectas en la circunferencia
M
N.
.
.
H
L.
D.
es tangente a la circunferencia
es exterior a la circunferencia
es secante a la circunferencia
MN
LD
ABes el punto de tangenciaH
13.
14. Teoremas importantes
Teorema 1:
Toda recta tangente a una circunferencia es perpendicular al
radio que contiene el punto de tangencia.
.O
F.
Círculo de centro O y radio OF
OF
15. Teoremas importantes
Teorema 2:
En una circunferencia, toda recta que contenga al centro y sea
perpendicular a una cuerda, biseca la cuerda.
.O
A
si AB entonces AM MB
.
B
M
16. Ejercicios
Dada la siguiente figura, complete lo que se le solicita.
Dos secantes:________
Tres cuerdas:________
Una tangente:________
Dos radios:__________
Un punto de tangencia:_____
Un diámetro:________
BG y
LR
CE
MR MG
,
,
JH
NR
F
BG SD,
19. Teoremas importantes
Teorema N°3:
Teorema del las Secantes Sean PA y PB dos secantes, entonces:
Toda la primera secante PA * su segmento externo PD es igual
a toda la segunda secante PB * su segmento externo PC
20. Teoremas importantes
Teorema N°4:
Teorema del la Tangente y Secantes sean PA una tangente y PC
una secante, entonces: la tangente al cuadrado PA es igual a
toda la secante PC por su segmento externo PD
22. Teoremas importantes
Teorema N°6:
Teorema de las Cuerdas sean AB y CD dos cuerdas, entonces:
El producto de los segmentos determinados en la primera
cuerda AP * PB es igual al productos de los segmentos
determinados en la segunda cuerda CP * PD
23. REPASO DE TEMAS ESTUDIADOS.
TRIGONOMETRÍA.
PLANES DE APOYO.
Matemáticas
grado 11
24. Todos se preguntan que son las matemáticas
y de donde provienen aquí encontrara su
respuesta
Matemática: es la disciplina que estudia,
mediante el razonamiento deductivo, las
propiedades de los entes abstractos, tales
como los números, las figuras geométricas,
etc...,así como las relaciones que dichos
entes guardan entre sí. Suele decirse que las
matemáticas nacieron en Grecia hacia el año
600 ADC Pero esta afirmación es solo
parcialmente verdad
25. Matemática: trigonometría
Que es la trigonometría?
trigonometría, rama de las matemáticas que
estudia las relaciones entre los lados y los ángulos
de triángulos, de las propiedades y aplicaciones de
las funciones trigonométricas de ángulos. las dos
ramas fundamentales son la trigonometría plana,
que se ocupa de figuras contenidas en un plano, y
la trigonometría esférica, que se ocupa de
triángulos que forman parte de la superficie de una
esfera.
26. Que es un Angulo?
el Angulo es la porción de plano delimitada por dos
semirrectas del mismo origen
Los ángulos se identifican por 3 letras donde :
La letra central corresponde al vértice
Las otras 2 letras son puntos cualquiera de las
semirrectas que lo forman
27. Los ángulos: se clasifican en
Angulo recto : mide 90 gradosAngulo agudo: mayor que 0 menor que 90
Angulo obtuso: mayor que 90 menor que 180 Angulo llano: mide 180 grados
29. Ángulos : complementarios y suplementarios
son complementarios cuando la suma de sus valores es un
ángulo recto, es decir, 90 grados sexagesimales.
Dos ángulos son suplementarios cuando la suma de sus valores es
igual a la de dos rectos, es decir(180º).
30. Como saber si un ángulo es complementario o
suplementario.
Dos ángulos son complementarios si la suma de sus
ángulos es igual a 90°.
Si conocemos un ángulo, su ángulo complementario se
puede encontrar restando la medida del mismo a 90o.
Ejemplo: ¿Cuál es el ángulo complementario de 43o?
Solución: 90° - 43° = 47°
Dos ángulos son suplementarios si la suma de sus grados es
igual a 180o.
Si conocemos un ángulo, su ángulo suplementario se puede
averiguar restando la medida del mismo a 180o.
Ejemplo: ¿Cuál es el ángulo suplementario de 143o?
Solución: 180° - 143° = 37°
32. ANGULOS CUADRANTALES
EJEMPLOS:
A) sen 90º. Solución: Como sen q = y, sen 90º = 1 (la coordenada en y).
B) cot 180º. Solución: Como cot q = x/y, cot 180º = –1/0 = indefinida
C) sec 360º. Solución: Como sec q = 1/x, sec 360º = 1/1 = 1
35. IDENTIDADES:
En matemática, las identidades trigonométricas son
igualdades que involucran funciones trigonométricas,
verificables para cualquier valor de las variables que se
consideren (es decir para cualquier valor que pudieran
tomar los ángulos sobre los que se aplican las funciones).
36. IDENTIDADES
Sec A = 1/Cos A; Cos A Sec A = 1
CscA = 1/SenA; Sen A Csc A = 1
Tan A = Sen A/Cos A
Tan A Cot A = 1
Cot A = Cos A/Sen A
Sen²A+Cos²A = 1
Sen²A=1-Cos²A
Cos²A=1-Sen²A
Tan²A+1=Sec²A
Tan²A=Sec²A-1
1=Sec²A-Tan²A
Cot²A+1=Csc²A
Cot²A=Csc²A-1
1=Csc²A-Cot²A
37. ANGULOS
Ángulos Dobles
sen2A=2senA cos A
cos2A=cos²A-Sen²A
tan2A=2TanA/1-Tan²A=Sen2A/Cos2A
Csc2A=1/Sen2A
Sec2A=1/CoS2A
Cot2A=Cos2A/Sen2A
38. IDENTIDADES
Ángulos Medios
sen(1/2) A=√(1-cosA)/2
Csc(1/2) A= √(1+cosA)/2
Tan(1/2) A = √(1-cosA)/(1+cosA)=Sen 2A/cos 2A
Csc(1/2 )A = √1/sen1/2 A
Sec ( ½) A = √ 1 /cos1/2 A
Cot (½ A) = √cos1/2 A/sen1/2 A
39. IDENTIDADES
Suma y/o Resta De Ángulos
sen(A±B) =sen A cos B ± Sen B Cos A
Csc(A ±B) = 1/sen (A+B)
Cos(A+B) = cosA cosB ±senA senB
Sec(A ±B) = 1/cos (A ±B)
Tan(A ±B) = TanA ±TanB/1 ±TanA TanB
Cot(A ±B) = Cos(A ±B)/Sen(A ±B)
41. Ley del Seno
En todo triángulo se da la siguiente relación entre la
longitud de sus lados A, B y C y el seno de sus
respectivos ángulos opuestos a, b y c
a/sin A = b/Sin B = c/Sin C
42. Ley del Coseno
En todo triángulo «El cuadrado de un lado es igual
a la suma de los cuadrados de los otros lados menos
el doble del producto de estos lados por el coseno del
ángulo comprendido...»
44. Graficas de funciones trigonométricas
Se usa esta ecuación para graficar.
y = ±C ±A sen o cos B(∞±D)
C= desplazamiento vertical
A= amplitud
B=numero de ciclos
D=desplazamiento horizontal
51. TRIANGULOS
Que es un triángulos ?
Porción de plano limitada por 3 líneas que se cortan
de dos en dos, en un punto común llamado vértice,
tiene 3 vértices y 3 lados.
52. TRIANGULOS
Según sus lados como se define un triangulo ?
• Equilátero: tres lados iguales
• Isósceles: dos lados iguales.
• Escaleno: tres lados desiguales.
53. TRIANGULOS
Según sus ángulos los triángulos se clasifican
• Acutángulo: tres ángulos agudos
• Rectángulo: un ángulo recto
• Obtusángulo: un ángulo obtuso
54. TRIANGULOS
El área de un triangulo siempre se coloca en unidades cuadradas
El Área de un triangulo es = Base * altura sobre 2
Subperimetro: el perímetro dividido entre 2
El perímetro se saca sumando todos los lados del triangulo.
Cateto al cuadrado+cateto al cuadrado=hipotenusa al cuadrado
Otra forma de sacar el Área de un triangulo es
A=√S(S-L1 )(S-L2 )(S-L3 )
55. TRIANGULOS
Ortocentro :
Se denomina ortocentro al punto donde se cortan
las tres alturas del triangulo.
ortocentro
57. GEOMETRIA: ANALITICA
Que es la geometría Analítica y para que nos sirve ?
se conoce como geometría analítica al estudio de
ciertos objetos geométricos mediante técnicas
básicas del Análisis matemático y del Algebra.
lo novedoso de la geometría analítica es que
permite representar figuras geométricas mediante
formulas del tipo f(x,y)=0 donde f representa una
función
58. CIRCULO
Centro (0 ,0)
X² + Y² =r²
Centro (h , k)
(x-h) ² +(y-k) ²= r²
Diámetro = 2 veces el radio
59. CIRCULO
Distancia entre 2 puntos :
D=√(x2-x1)²+(y2-y1)²
Distancia de un punto a
una línea :
D=/Ax+By+C/
√A²+B²
60. CIRCULO
Punto Medio :
Pm: (xm= x1+x2 /2)
(ym= y1+y2 /2)
Área del Circulo :
πr²
Formula General :
X²+Y²+Bx+Cy+D=0
Circunferencia o
perímetro : 2πr
61. CIRCULO
Cuando:
El radio al cuadrado es mayor que 0,es Circulo real.
El radio al cuadrado es igual que 0, es Punto.
El radio al cuadrado es menor que 0 , es Circulo
Imaginario.
62. CIRCULO
Área sector :
πr²n / 360
Área Segmento :
A Sector - AΔ
Longitud del sector
2πrn/360
Área Corona Circular
πr² - πR²
Β = π(R² - r²)
63. ANGULOS Y LINEAS A UN CIRCULO
Líneas tangentes trazadas desde un punto exterior
con iguales, tienen la misma medida
∞= arco mayor – arco menor
2
L1=L2
64. ANGULOS Y LINEAS A UN CIRCULO
Líneas secantes :
Trazados desde un punto exterior
Secante Secante1 * Seg.Ext1= Secante2* Seg.Ext2
B = arco mayor – arco menor
2
65. ANGULOS Y LINEAS A UN CIRCULO
Línea tangente y secante :
Trazados desde un punto exterior
Tan² = Secante* Seg.Ext
66. ANGULOS Y LINEAS A UN CIRCULO
Cuerdas que se cortan dentro de un circulo
68. ANGULOS
Punto a una razón dada = (xr = x1+r(x2-x1)
(yr = y1+r(y2-y1)
Area del triangulo: AΔ= B*h /2
A =√S(s-a)(s-b)(s-c) S=a+b+c / 2
AΔ equilatero = l²√3 / 4
69. ANGULOS
Dados 2 puntos (x1,y1)(x2,y2 )
. Se busca la pendiente
1) M = y 2–y1
x2 - x1
2) y – y1 =m(x – x1 )
Dado un punto y la pendiente
1) Encuentras M
2) P(x1,y1)
3) y – y1 =m(x – x1 )
70. ANGULOS
Dada la pendiente (m) y el intercepto con el eje y (b)
y=mx+b
Dado los 2 intercepto (a,b)
x/a + y/b=1
Forma general: Ax+By+C = 0
Para dar la inclinación de la línea
Pendiente = tan β
71. ANGULOS
Ecuación de la mediatriz:
Mediatriz: es la linea que sale del punto medio de
un segmento en forma perpendicular.
1) Hallo punto medio del segmento
2) Hallo pendiente de ese segmento y la paso a
perpendicular
3) Hago la ecuación: y-y1 = m(x-x1)
72. ANGULOS
Ecuación de la Altura :
1) Hallo pendiente del segmento donde llega y la
paso a perpendicular
2) Hago la ecuación con M y el punto donde sale la
altura : y-y1=m(x-x1)
73. ANGULOS
Ecuación de la mediana :
Mediana: es el segmento que tiene por extremos, un
vértice y el punto medio del lado opuesto.
1) Hallo punto medio del segmento donde
2) Busco pendiente del punto medio, y punto de donde
sale
3) Escribo la ecuación (y-y1)=m(x-x1)
74. ANGULOS
Líneas paralelas tienen pendientes iguales
Líneas perpendiculares: inversas y signo contrario
m= -1/m
Línea paralela al eje x tiene m = 0
Línea paralela al eje y tiene m = 1/0
75. CONICAS
Elipse
a=punto final eje mayor
sus coordenadas se
llaman vértice
b=punto final eje menor,
sus coordenadas se
nombran B
c= foco c² = a² – b²
Lr= lado recto lr=2b²/a
E=exentridad e= c/a
e <1 e = c/a
Horizontal Vertical
x ²+ y ²= 1 x ²+ y ² =1
a ² b ² a ² b²
76. CONICAS
a=punto final eje mayor ,
sus coordenadas se llaman
vertical
b=punto final eje menor,
sus coordenadas se
nombran B
c= foco c ²= a ²- b ²
Lr= lado recto lr= 2b ²/a
Excentridad e=c/a debe
ser menor que 1
a= punto final eje real o
transversal, sus
coordenadas se llaman
vértice
b= punto final eje
conjugado o imaginario,
sus coordenadas se llaman
B
C= foco c ²=a ²+b ²
Lr= lado recto lr= 2b ²/a
E=c/a debe ser mayor
que 1
77. CONICAS
Elipse E Hipérbola Elipse E Hipérbola
Horizontal Vertical
C (0,0) C (0,0)
v (±a,0) v (0, ±a)
(0,±b) β (±b,0)
f (±c,0) f (0, ±c)
Pf (±c, ±1/2L) pf (±1/2Lr ±c)
Siempre c < a Siempre c > a
78. CONICAS
Eje mayor o eje real o transversal= 2a
Eje menor o eje conjugado o imaginario = 2b
Elipse hipérbola
79. CONICAS
Distancia focal 2c
El centro es el punto medio entre los dos vértices (v),
los dos puntos finales del eje menor o conjugado (B)
o los dos focos (F).el foco es el punto medio entre los
dos puntos finales.
80. CONICAS
ELIPSE C (h,k) HIPERBOLA
Horizontal Horizontal
(x – h) ² + (y – k)² = 1 (x – h) ² - (y – k) = 1
a ² b ² a ² b ²
Vertical Vertical
(x – h) ² + (y – k) ² = 1 (y – k) ² - (x – h) ²
b ² a ² a ² b ²
81. CONICAS
Elipse - Hipérbola Elipse – Hipérbola
C (h,k) Horizontal C (h,k) Vertical
v (h±a,k) v (h,k±a)
(h,k±b) β (h±b,k)
f (h±c,k) f (h,k±c)
pf (h±c,k1/2Lr) pf (h±1/2Lr,k±c)
82. CONICAS
Parabola e = 1
v (0,0) v (h,k)
y²= 4ax (y – k ) ² =4ª(x – h)
Lr = 4ª Lr= 4a
f (a,0) f ( h +a, k)
D: x= -a D: x= h – a
pf ( a, ±2ª) pf (h+a,k ±2a)
vf = vd
Distancia del vertice al foco = Distancia de vertice a directriz
83. CONICAS
Vértice es el punto medio entre foco y directriz. Foco
es el punto medio entre los 2 puntos finales.
y² = -4ac (y – k)²= -4ac (x – h)
f (- a,0) f (h-a, k)
D: x =a D: x= h +a
pf (-a,±2ª) pf (h-a,k±2ª)
88. ECUACION DE LA LINEA
cuando te dan dos puntos. Se usa esta formula:
M = y2 - y1/ x2 - x1
cuando te dan la ecuación Ax + By + C = 0. se usa
esta formula :
M = -a/ b
89. ECUACION DE LA LINEA
Aplicamos esta ecuación cuando tenemos
Y= mx+b Y-Y1 = m(x – x1 )
M = pendiente este lo uso cuando me un
y= intercepto punto y la pendiente o me
dan los puntos.
90. ECUACION DE LA LINEA
Cuando nos dan los intercepto y la formula general.
Ax + By + C = 0 x + y = 1
Formula general de a b
de una linea
91. GENERALIDADES
Para hallar el intercepto en y:
Igualo x = 0 y busco y
para hallar el intercepto en x :
igualo y = 0 y busco x
92. GENERALIDADES
Para hallar la pendiente y la inclinación aplicamos la
siguiente ecuación :
m = y2-y1 / x2-x1
y con la respuesta pongo en la calculadora shift tan de
la respuesta:
Tan B =m
93. GENERALIDADES
Para hallar la simetría:
X = -x misma ecuación simétrica eje y
Y = -y misma ecuación simétrica eje x
Para hallar simetría en el origen:
X=-x, y=-y misma ecuación simétrica origen
