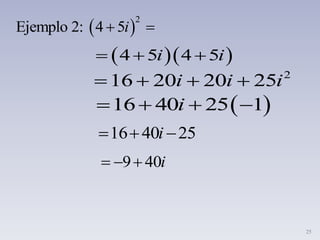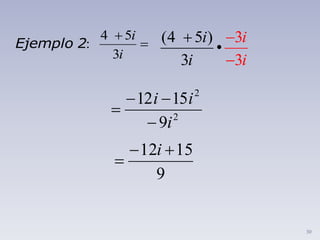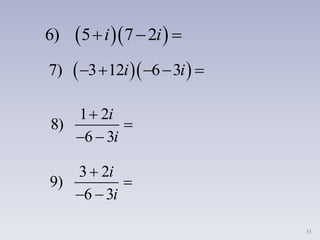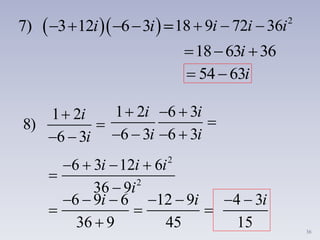i. El documento define números imaginarios y complejos, y explica cómo operar con ellos. ii. Incluye las definiciones de unidad imaginaria, potencias de i, y números complejos. iii. Explica cómo sumar, restar, multiplicar y dividir números complejos siguiendo reglas similares a las operaciones con polinomios.

1. 1

2. 2
OBJETIVOS:
1. Definir unidad imaginaria.
2. Conocer y simplificar potencias de i.
3. Definir el conjunto de los números complejos.
4. Operar con los números complejos.

3. 3
DEFINICIÓN:Los Números Imaginarios surgen de la
necesidad de resolver ecuaciones cuadráticas sin
solución en el campo real.
Este conjunto se representa por I
 Este conjunto posee elementos que se
obtienen a partir de raíces cuadradas con
cantidad subradical negativa.
7 3 2 3 10 

4. 4
Definición:
Entenderemos como Unidad Imaginaria a:
La que se conoce como Raíz Imaginaria.
i= -1
Nota: 2
i =-1

5. NÚMEROS IMAGINARIOS
 Luego:
 
16
16 1
16 1
4i
 
  
  


6.  E inventaron un número cuyo cuadrado es -1
 después del año 1777, Euler lo denominó
con la letra “i”.
2
i =-1

7. 7
POTENCIAS DE I:
1. Divida el exponente por 4 y el resultado será elevado al resto de
la división.
2. luego para simplificar use;
3. Sí
2
i =-1
 3 2
i =i i=-1 i=-i
  4 2 2
i =i i = -1 -1 =1
Este último resultado hace que las potencias de “i” solo
tengan como resultados a: i, -i, 1 y -1
0
i =1
1
i =i
n 4m+p p
i =i =i
i= -1

8. 8
EJEMPLOS:
4 1 2 2
1i i
  g
6: 4 1
2

4 2 3 3
i i i
  g11
1)i 
540
2) i 
4 135 0 0
1i i
 g
11: 4 2
3

540: 4 135
14
020
0

6
3)i 

9. 9
3
i 
13
4) i  i
227
5) i  i
285
6) i 
1
i
1127
7) i  i
285 4 71 1 g
i
1127 4 281 3 g
3
i 

10. 10
Calcule las siguientes raíces:
4 1  
11 i
25 1  
1) 4 
2) 25 
3) 12 
4) 11 
i2
i5
2 3 i4 3 1  
Raíces pares de Números Negativos

11. NÚMEROS COMPLEJOS
 Hallar los números reales que verifican que
la suma entre el quíntuplo de su cuadrado y
20, es igual a cero.
 En símbolos:
2
5 20 0x  

12. NÚMEROS COMPLEJOS
 Al resolver la ecuación obtenida, nos damos
cuenta que la raíz cuadrada de un número
negativo no existe en los reales, por lo
tanto esta ecuación no tiene solución en este
conjunto, es decir que no existe ningún
número real que resuelva este problema.
(Sin solución real)
2
5 20 0x  

13. NÚMEROS COMPLEJOS
 Para que la ecuación anterior tenga solución,
los matemáticos buscaron una ampliación
del conjunto de los Números Reales (IR).
 A este Conjunto se definió como los
Números Complejos:
 / , ;a bi a bi   £ ¡ I

14. © copywriter
14
i) Los números reales y los
imaginarios están incluidos en
el conjunto ampliado.
ii) Las propiedades del
conjunto real se siguen
cumpliendo en el conjunto
ampliado.
Sus características son:

15. NÚMEROS COMPLEJOS
 Se llama número complejo a un número “z”
que puede escribirse de la forma
 a y b son números reales
 Al número a se le llama parte real (a=Re[z])
 Al número b se le llama parte imaginaria
(b=Im[z])
z=a+bi
a+bi (a,b)

16. IGUALDAD DE NÚMEROS COMPLEJOS:
 Dos Números complejos son iguales si y
sólo si, tienen igual parte real e igual parte
imaginaria
 si
 Entonces:
1 2z =z
       1 2 1 2Re z =Re z Im z =Im z
Ó sí a + bi = c + di entonces a = c y b = d.

17. 17
Ejemplos de Números Complejos:
i35)1 
i47)2 
i61)3 
i5)4
7)5

18. 18
 81)5   1 4 2 1 
1 2 2 i 
1 4 2 1    

19. 19
Ejemplo:
Determine el valor de y de si
  ibia 5626 
66Si a 2 5y b  
0a
2
5
b
a b

20. 20
OPERACIONES CON NÚMEROS COMPLEJOS
   a bi c di  1.Suma:
   idbca 
   Ej 5em 1: 6plo 2   i i
   5 6 1 2    i
i11

21. 21
   a bi c di  2.Resta:
   idbca 
   3Ejemplo 1: 2 6 3    i i
   3 2 6 3i i   
9 5i 
   a bi c di    
Obs:La resta se cambia a la suma del opuesto del sustraendo.

22. 22
   Ejemplo 2: 8 18 5 50     
   8 3 2 5 5 2i i   
   8 3 2 5 5 2i i    
3 8 2 i 

23. 23
   a bi c di g3.Multiplicación:
   ac bd ad bc i   
Nota: La multiplicación se puede llevar a cabo como si
fuera una multiplicación de polinomios.
  a bi c di   ac ad i  bc i  2
bd i 
   1ac ad bc i bd    
   ac bd ad bc i   

24. 24
  Ejemplo 1: 4 2 3 5  i i
2
1062012 iii 
12 14 10i  
i1422
 12 20 6 10 1i i    

25. 25
 
2
Ejemplo 2: 4 5 i
254016  i
i409
  4 5 4 5i i  
2
16 20 20 25i i i   
 16 40 25 1i   

26. 26
 
3
Ejemplo 3: 2 3 i
46 9i  
   
2
2 3 2 3i i 
  2
4 12 9 2 3i i i   
   4 12 9 1 2 3i i    
  4 12 9 2 3i i   
  5 12 2 3i i   
2
10 15 24 36i i i    
10 15 24 36i i    

27. 27
.El conjugado de
Conjugado de un C
z=a+bi sedefin
ompl
e po
ejo:
Definició
r Z=a+bi=a
n
-bi
:
Encuentra el conjugado de cada
Ejemplo
núm
s:
ero:
1. 2 4
2. 2 4
3. 64
4. 12 24
5. 13
i
i
i
i
 
 

 

i42
2 4i
64i
12 24i
13

28. 28
8 7
:
1 3
i
i



Ejemplo 1
(8 7 )
•
(1 3 )
(1 3 )
(1 3 )
ii
i i


2
2
91
217248
i
iii



La División se hace multiplicando por el conjugado
del denominador. (similar a la racionalización)
 
 
a bi
c di



4.División: .
a bi c di
c di c di
   
   
 

  

29. 29
 
 
8 17 21 1
1 9 1
i  

 
8 17 21
1 9
i 

 10
1729 i

i
10
17
10
29


30. 30
4 5
:
3
i
i

Ejemplo 2 (4 5 )
•
3
3
3i i
i i 

2
2
9
1512
i
ii



9
1512 

i

31. 31
9
1512 

i
9
15
9
12


 i
3
5
3
4
 i
i
3
4
3
5


32. 32
Ejercicios:
Resuelve la operación indicada.
   1) 5 7 2i i   
   2) 3 12 6 3i i     
   3) 12 23 16 13i i    
   4) 13 32 36 53i i     
  5) 3 2 6 3i i   

33. 33
  6) 5 7 2i i  
  7) 3 12 6 3i i    
1 2
8)
6 3


 
i
i
3 2
9)
6 3


 
i
i

34. 34
   1) 5 7 2i i    12 i
   2) 3 12 6 3i i     
   3 12 6 3    i i 3 15  i
   3) 12 23 16 13i i    
   12 23 16 13   i i 28 36 i

35. 35
   4) 13 32 36 53i i      49 21  i
  5) 3 2 6 3i i    2
18 9 12 6   i i i
 18 21 6 1    i
12 21   i
  6) 5 7 2i i   2
35 10 7 2  i i i
35 3 2  i
37 3  i

36. 36
  7) 3 12 6 3i i     2
18 9 72 36   i i i
18 63 36  i
54 63  i
1 2
8)
6 3


 
i
i
1 2 6 3
6 3 6 3
  

   
i i
i i
2
2
6 3 12 6
36 9
   


i i i
i
6 9 6
36 9
  


i 12 9
45
 
 
i 4 3
15
  i

37. 37
3 2
9)
6 3


 
i
i
3 2 6 3
=
6 3 6 3
  
   
g
i i
i i
2
18 9 12 6
=
36 9
   

i i i
18 3 6
=
36 9
  

i
24 3
=
45
  i 8
=
15
  i

38. REPRESENTACIÓN GRÁFICA:
 Para representar un número complejo, de la
forma se utiliza un sistema de
coordenadas rectangulares, en el cual la
parte real se representa en el eje horizontal y
la imaginaria en el eje vertical.
 Obs:
a+bi
a+bi (a,b)

39. Ejemplos:

41. Módulo de un Complejo:
 Es la distancia entre el origen y el punto
que representa al número complejo.
 El módulo de un número complejo
está definido como:
 Ejemplo:
2 2
a+bi = a +b
2 2
(-4) +2 = 20 =2 5-4+2i
a+bi