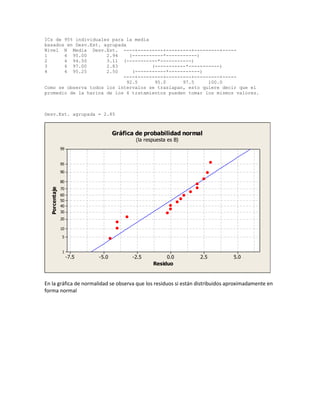
Este documento presenta los resultados de un experimento para determinar si diferentes marcas de harina producen la misma viscosidad en masas de galletas. Se midió la viscosidad de 16 masas, 4 de cada marca de harina. El análisis de varianza encontró que no hay diferencias significativas en la viscosidad entre las marcas. Adicionalmente, pruebas posteriores también indicaron que las varianzas de viscosidad entre marcas son iguales.

1. Caso 1 balanceado
En una determinada fábrica de galletas se desea saber si las
harinas de sus cuatro proveedores producen la misma viscosidad en
la masa. Para ello, produce durante un día 16 masas, 4 de cada tipo
de harina, y mide su viscosidad. Los resultados obtenidos son:
Acomodando los datos aleatoriamente
Proveedor A Proveedor B Proveedor C Proveedor D
98
97
99
96
91
90
93
92
96
95
97
95
95
96
99
98
Variable respuesta: viscosidad
¥ Factor: Proveedor
¥ Tratamientos: 4
¥ Modelo unifactorial de efectos fijos equilibrado
Criterio de calidad: mayor mejor

2. Gráfica de caja de B
99
98
97
96
B
95
94
93
92
91
90
1
2
3
4
A
Se observa que las medias de viscosidad de las harinas de los proveedores 1,2 y 4 son iguales
ANOVA
ANOVA unidireccional: B vs. A
Fuente
GL
SC
CM
A
Error
3
12
97.75
8.15
Total
15
S = 2.854
F
P
14.19
4.73
0.58
0.639
111.94
R-cuad. = 12.67%
R-cuad.(ajustado) = 0.00%
Como se observa P=.639 y esta distante de cero significa que no le es
significante la viscosidad sobre el tipo de harina.
Como observamos en R-cuad. = 12.67%
es poco confiable el modelo.

3. ICs de 95% individuales para la media
basados en Desv.Est. agrupada
Nivel N Media Desv.Est. ----+---------+---------+---------+----1
4 95.00
2.94
(-----------*-----------)
2
4 94.50
3.11 (-----------*-----------)
3
4 97.00
2.83
(-----------*-----------)
4
4 95.25
2.50
(-----------*-----------)
----+---------+---------+---------+----92.5
95.0
97.5
100.0
Como se observa todos los intervalos se traslapan, esto quiere decir que el
promedio de la harina de los 4 tratamientos pueden tomar los mismos valores.
Desv.Est. agrupada = 2.85
Gráfica de probabilidad normal
(la respuesta es B)
99
95
90
Porcentaje
80
70
60
50
40
30
20
10
5
1
-7.5
-5.0
-2.5
0.0
Residuo
2.5
5.0
En la gráfica de normalidad se observa que los residuos si están distribuidos aproximadamente en
forma normal

4. vs. orden
(la respuesta es B)
3
2
Residuo
1
0
-1
-2
-3
-4
-5
1
2
3
4
5
6
7
8
9
10 11
Orden de observación
12
13
14
15
16
En la gráfica de valores estimados se observan los residuos dispersos, quiere decir sin patrón de
embudo por lo tanto se cumple la independencia

5. vs. ajustes
(la respuesta es B)
3
2
Residuo
1
0
-1
-2
-3
-4
-5
94.5
95.0
95.5
96.0
Valor ajustado
96.5
97.0
Se observa en la gráfica contra el orden de corrida que el experimento si se llevó a cabo una forma
completamente aleatoria
CÁLCULO POTENCIA DE LA PRUEBA
Método de la mínima diferencia significativa (LSD)
Ho: µi=µj
H1: µi≠µj
Ῡ1- Ῡ2= 0.5
Ῡ1- Ῡ3=-2
Ῡ1- Ῡ4=-0.25
Ῡ2- Ῡ3=-2.5
Ῡ2- Ῡ4= -0.75
Ῡ3-Ῡ4=1.75
t.(025,12)
=2.179 Obtenido de la tabla t

6. |Ῡ1-Ῡ3|= 2 <LSD(4.39)
|Ῡ1-Ῡ4|= 0.25 <LSD(4.39)
|Ῡ2-Ῡ3|= 2.5 <LSD(4.39)
|Ῡ2-Ῡ4|= 0.75 <LSD(4.39)
|Ῡ3-Ῡ4|= 1.75 <LSD(4.39)
Como todos los valores son menores al LSD se acepta Ho y esto explica que todas las harinas
producen la misma viscosidad ya que son iguales sus medias.
Prueba de Bartlett
s^2p = {3(2.94) + 3(3.11) +3(2.83) + 3(2.50)} / 12 = 2.845
q = (12 ) log10 (2.845) – 3 {log10 (2.94) + log10(3.11) +log10(2.83) + log10(2.50) = 0.016
c=1+((1/9(4/3-1/12))=1.13

7. 2.3026(.016/1.13)=0.032
(.05,3)=7.81
Se sigue aceptando Ho por ser menor el valor de
lo que indica que las cuatro varianzas son iguales.
LEVENE^S
y
i
~
yi
yi n
n 1
2
yi n
2
2
yi(16/2) +
impar
2
1
par
.032, que en el estadístico de prueba,

9. CASO 2 DESBALANCEADO
En una determinada fábrica de galletas se desea saber si las
harinas de sus cuatro proveedores producen la misma viscosidad en
la masa. Para ello, produce durante un día 16 masas, 4 de cada tipo
de harina, y mide su viscosidad. Los resultados obtenidos son:
Acomodando los datos aleatoriamente
Proveedor A Proveedor B Proveedor C Proveedor D
98
97
99
91
90
93
92
95
97
95
99
98
Variable respuesta: viscosidad
¥ Factor: Proveedor
¥ Tratamientos: 4
¥ Modelo unifactorial de efectos fijos equilibrado
Criterio de calidad: mayor mejor

10. Diagrama de caja
Gráfica de caja de visco
99
98
97
visco
96
95
94
93
92
91
90
1
2
3
4
trat
Se observa que las medias de viscosidad de las harinas de los proveedores 1,2 y 4 son iguales
ANOVA unidireccional: viscosidad vs. Tratamiento
Fuente
GL
A
Error
3
12
Total
15
S = 3.403
SC
CM
18
92.7
F
P
6.0 0.52
11.6
0.682
110.66
R-cuad. = 16.27%
R-cuad.(ajustado) = 0.00%
Como se observa P=.682 y está distante de cero significa que no le es
significante la viscosidad sobre el tipo de harina.
Como observamos en R-cuad. = 16.27%
es poco confiable el modelo.

11. ICs de 95% individuales para la media
basados en Desv.Est. agrupada
Nivel N Media Desv.Est.
--+---------+---------+---------+------1
3 94.67
3.51
(---------------*--------------)
2
3 94.00
3.61
(--------------*--------------)
3
4 97.00
2.83
(------------*------------)
4
2 95.00
4.24
(------------------*-----------------)
--+---------+---------+---------+------90.0
93.0
96.0 99.0
Desv.Est. agrupada = 3.40
Como se observa todos los intervalos se traslapan, esto quiere decir que el
promedio de la harina de los 4 tratamientos pueden tomar los mismos valores.
Gráfica de probabilidad normal
(la respuesta es visco)
99
95
90
Porcentaje
80
70
60
50
40
30
20
10
5
1
-8
-6
-4
-2
0
Residuo
2
4
6
8
En la gráfica de normalidad se observa que los residuos si están distribuidos aproximadamente en
forma normal

12. vs. orden
(la respuesta es visco)
4
3
2
Residuo
1
0
-1
-2
-3
-4
1
2
3
4
5
6
7
8
Orden de observación
9
10
11
12
En la gráfica de valores estimados se observan los residuos dispersos, quiere decir sin patrón de
embudo por lo tanto se cumple la independencia

13. vs. ajustes
(la respuesta es visco)
4
3
2
Residuo
1
0
-1
-2
-3
-4
94.0
94.5
95.0
95.5
Valor ajustado
96.0
96.5
97.0
Se observa en la gráfica contra el orden de corrida que el experimento si se llevó a cabo una forma
completamente aleatoria

14. CÁLCULO POTENCIA DE LA PRUEBA
Método de la mínima diferencia significativa (LSD)
Ho: µi=µj
H1: µi≠µj
Ῡ1- Ῡ2= .66
Ῡ1- Ῡ3=-2.34
Ῡ1- Ῡ4=-0.34
Ῡ2- Ῡ3=-3
Ῡ2- Ῡ4= -1
Ῡ3-Ῡ4=2
t.(025,8)
=2.306 Obtenido de la tabla t
|Ῡ1-Ῡ2|= .66< LSD(3.20)
|Ῡ1-Ῡ3|= -2.34<LSD(3.20)
|Ῡ1-Ῡ4|= -.34 <LSD(3.20)
|Ῡ2-Ῡ3|= -3 <LSD(3.20)
|Ῡ2-Ῡ4|= -1 <LSD(3.20)
|Ῡ3-Ῡ4|= 2 <LSD(3.20)
Como todos los valores son menores al LSD se acepta Ho y esto explica que todas las harinas
producen la misma viscosidad ya que son iguales sus medias.
Prueba de Bartlett

15. s^2p = {3(2.94) + 3(3.11) +3(2.83) + 3(2.50)} / 12 = 2.845
q = (12 ) log10 (2.845) – 3 {log10 (2.94) + log10(3.11) +log10(2.83) + log10(2.50) = 0.016
c=1+((1/9(4/3-1/12))=1.13
2.3026(.016/1.13)=0.032
(.05,3)=7.81
Se sigue aceptando Ho por ser menor el valor de
lo que indica que las cuatro varianzas son iguales.
LEVENE^S
y
i
~
yi
yi n
n 1
2
impar
yi n
2
2
2
1
par
.032, que en el estadístico de prueba,

16. yi(16/2) +