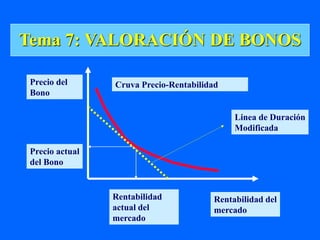
Este documento describe conceptos clave relacionados con la valoración y análisis de bonos. Explica cómo calcular el valor intrínseco de un bono descontando sus flujos de efectivo futuros a una tasa de descuento apropiada. También cubre cómo los cambios en las tasas de interés afectan el precio de los bonos y cómo medir la duración y el riesgo de tipo de interés. Además, proporciona ejemplos numéricos para ilustrar estos conceptos.

1. Tema 7: VALORACIÓN DE BONOS
Rentabilidad del
mercado
Rentabilidad
actual del
mercado
Linea de Duración
Modificada
Cruva Precio-Rentabilidad
Precio actual
del Bono
Precio del
Bono

2. Activos de Renta Fija
 Deuda a medio/largo plazo (bonos)
- Los pagos realizados a los tenedores de
bonos están fijados previamente.
 Acciones Preferentes
- Los dividendos preferentes son
establecidos previamente y pueden ser
acumulativos.

3. Características de los Bonos
 Pagan un cupón fijo (interés)
 Los pagos son en intervalos temporales
fijos (normalmente cada 6 meses)
 Realizan un pago al vencimiento por el
nominal
0 1 2 . . . n
I I I I I I+M

4. Ejemplo: Bonos Coca Cola
9s/2049
 Valor nominal = 1000 $
 Cupón = 9% anual sobre VN .
= 90 $ anuales (45 $ cada 6 meses).
 Vencimiento = 20 años.
 Emitido por Coca Cola.
0 1 2 . . . n
45$ 45$ 45$ 45$ 45$ 45$+1000$

5. Tipos de Bonos
 Obligaciones - Bonos sin asegurar.
 Obligaciones Subordinadas - Deuda
subordinada en caso de insolvencia.
 Bonos Hipotecarios - Bonos con garantía real.
 Bonos Cupón Cero - Realizan un único pago al
vencimiento: intereses + nominal.
 Bonos Basura (Junk Bonds) - Bonos de alto
riesgo con rating o calificación BB o inferior
según Moody´s o Standard and Poor´s.

6. Tipos de Bonos
 Eurobonos - Bonos denominados en una divisa
y emitidos en otro país. (Financiación en el
extranjero).
 Ejemplo - Suponga que Coca Cola decide
emitir 1,000 $ en bonos in España. Es una
emisión de bonos en $ USA, pero emitida en
otro país. ¿ A qué obedece este hecho?.
 Si los tipos de interés en España están más
bajos que en USA y,
 Para evitar la normativa de la SEC.

7. Bonos Convertibles
 Algunas emisiones de bonos tienen
la posibilidad de convertirse en
acciones.
 ¿ Supone esto un beneficio para el
inversor?
Evidentemente que si pués
incorpora flexibilidad.

8. El contrato de emisión del Bono
 Listado de todos los términos de la
emisión: cupón, nominal,
vencimiento, etc.
 Derechos sobre activos y resultados
que protegen al obligacionista en
caso de insolvencia de la empresa.
 Calificación o rating de la emisión.

9. Valoración de Bonos
 En general:
El valor intrínseco de un activo = el
valor presente de la estructura de
Flujos de Caja esperados descontados
a una apropiada tasa de rentabilidad
requerida por el inversor.
¿Puede el valor intrínseco de una
activo ser diferente de su valor de
mercado?

10. Valoración de Bonos
 Descontando la estructura de Flujos de
Caja a una tasa de rentabilidad requerida
por el inversor.
1)La estructura de cupones como una renta
o anualidad.
2) El valor nominal al vencimiento como un
pago simple.

11. Valoración de Bonos
 I = Cupón o interés.
 kb = Tasa de rentabilidad requerida por el
inversor (depende del riesgo del bono).
 Vb = Valor intrínseco del bono.
Vb =
I M
(1 + kb) (1 + kb)
t = 1
n
t n
+
S

12. Valoración de Bonos
Vb = I (FIVPA i, n) + M (FIVPA i, n)
+
Vb =
I M
(1 + kb) (1 + kb)
t = 1
n
t n
S

13. Ejemplo de Bono
 Una empresa emite bonos a 20 años de
valor nominal 1,000$ y pago de cupones
anuales. La rentabilidad de bonos de
similar riesgo actualmente en el
mercado es del 12%, por lo que decide
fijar un cupón del 12% de interés
nominal anual.
 ¿Qué precio de emisión deben tener los
bonos?

14. 0 1 2 3 . . . 20
1000
120 120 120 . . . 120
P/año = 1
N = 20
I% año = 12
VF = 1,000
A = 120
Solución VP = -1,000 $
Nota: Si el cupón = tasa de descuento, el
bono se emitirá a su valor nominal.

15. Ejemplo de Bono
Solución Matemática:
VP = A (FIVPA i, n ) + VF (FIVPA i, n )
VP = 120 (FIVPA .12, 20 ) + 1000 (FIVPA .12, 20 )
1
VP = A 1 - (1 + i)n + VF / (1 + i)n
i
1
VP = 120 1 - (1.12 )20 + 1000/ (1.12) 20 = 1000 $
0.12

16.  Supongamos que los tipos de interés en
el mercado desciende inmediatamente
después de la emisión de los bonos. La
tasa de retorno requerida para bonos de
similar riesgo desciende hasta el 10%.
 ¿ Qué repercusión tiene este hecho en el
precio de mercado de los bonos ?

17. P/año = 1
Modo = Pospagable
N = 20
I% año = 10
A = 120
VF = 1000
Solución VP = -1,170.27$
Nota: Si el cupón > tasa de descuento, el
bono se venderá con una prima (Plusvalía)

18. Ejemplo de Bono
Solución Matemática:
VP = A (FIVPA i, n ) + VF (FIVP i, n )
VP = 120 (FIVPA .10, 20 ) + 1000 (FIVP .10, 20 )
1
VP = A 1 - (1 + i)n + VF / (1 + i)n
i
1
VP = 120 1 - (1.10 )20 + 1000/ (1.10) 20 = 1,170.27 $
.10

19.  Supongamos que los tipos de interés en
el mercado aumentan inmediatamente
después de la emisión de los bonos. La
tasa de retorno requerida para bonos de
similar riesgo asciende hasta el 14%.
 ¿ Qué repercusión tiene este hecho en el
precio de mercado de los bonos ?

20. P/año = 1
Modo = Pospagable
N = 20
I% año = 14
A = 120
VF = 1000
Solución VP = -867.54 $
Nota: Si el cupón < tasa de descuento, el
bono se venderá con descuento (Minusvalía)

21. Ejemplo de Bono
Solución Matemática:
VP = A (FIVPA i, n ) + VF (FIVP i, n )
VP = 120 (FIVPA .14, 20 ) + 1000 (FIVPA .14, 20 )
1
VP = A 1 - (1 + i)n + VF / (1 + i)n
i
1
VP = 120 1 - (1.14 )20 + 1000/ (1.14) 20 = 867.54 $
0 .14

22. Supongamos cupones semestrales
P/año = 2
Modo = Pospagable
N = 40
I% año = 14
A = 60
VF = 1000
Solución VP = -866.68 $

23. Ejemplo de Bono
Solución Matemática:
VP = A (FIVPA i, n ) + VF (FIVP i, n )
VP = 60 (FIVPA .14, 20 ) + 1000 (FIVP .14, 20 )
1
VP = A 1 - (1 + i)n + VF / (1 + i)n
i
1
VP = 60 1 - (1.07 )40 + 1000 / (1.07) 40 = 866.68 $
.07

24. Rentabilidad al Vencimiento (TIR)
Yield To Maturity (YTM)
 Tasa de rentabilidad anual que el
inversor espera obtener de un bono si
lo mantiene hasta el vencimiento.
V = I (FIVPA i, n) + M (FIVP i, n)
b
Resolviendo, TIR=i

25. Ejemplo TIR
Suponga que pagamos 898.90 $ por un
bono de valor nominal 1,000 $ con
cupón del 10% al que le quedan 8 años
para el vencimiento y tiene pagos
semestrales.
¿ Cuál es la Rentabilidad al Vencimiento
o TIR?

26. P/año = 2
Modo = Pospagable
N = 16
VP = -898.90
A = 50
VF = 1000
Solución TIR= 12%

27. Ejemplo de Bono
Solución Matemática:
VP = A (FIVPA i, n ) + VF (FIVP i, n )
898.90 = 50 (FIVPA i, 16 ) + 1000 (FIVP i, 16 )
1
VP = A 1 - (1 + i)n + VF / (1 + i)n
i
1
898.90 = 50 1 - (1 + i )16 + 1000 / (1 + i) 16
i por aproximaciones sucesivas

28. Bonos Cupón Cero
No realizan pagos de cupones.
La rentabilidad del inversor
viene determinada por el
precio de emisión.

29. Ejemplo de Bonos Cupón Cero
Supongamos que un inversor paga 508 $
por un bono al que le quedan 10 años
hasta el vencimiento.
¿Cuál es la rentabilidad al vencimiento?
0 10
-508 $ 1000 $

30. P/año = 1
Modo = Pospagable
N = 10
VP = -508
VF = 1000
Solución: TIR = 7%
Ejemplo Bono Cupón Cero

31. Solución Matemática:
VP = VF (FIVP i, n )
508 = 1000 (FIVPi, 10 )
0.508 = (FIVPi, 10 )
VP = VF /(1 + i) 10
508 = 1000 /(1 + i)10
1.9685 = (1 + i)10
i = 7%
Bono Cupón Cero
0 10
VP = -508 VF = 1000

32. La información financiera:
Bonos de Empresas (Corporate Bonds)
Wall Street Journal Rentab.
Bonos Actual Vol. Cierre Varia.
Eckerd 9s 1/4 04 8.6 20 107 1/2 ...
¿ Cuál es la rentabilidad al vencimiento?
 P/año = 2, N = 12, VF = 1000, VP = -1,075 $,
 A = 46.25
 Solución: 7. 67%

33. La información financiera:
Bonos de Empresas (Corporate Bonds)
Wall Street Journal Rentab.
Bonos Actual Vol. Cierre Varia.
AlldC zr 09 ... 30 43 5/8 +2
¿ Cuál es la rentabilidad al vencimiento?
 P/año = 1, N = 11, VF = 1000, VP = -436.25 $,
 A = 0
 Solución = 7.83%

34. La información financiera :
Bonos del Tesoro (Treasury Bonds)
Maturity Ask
Return Mo/Yr Bid Asked Var. Yld
9 Nov 18 129,00 128,50 +13 6.43
 ¿Cuál es la rentabilidad al vencimiento de
los Bonos del Tesoro?
 P/año = 2, N = 40, VF = 1000, A = 45,
VP = - 1,287.50 (128.75% del nominal)
 Solución: 6.43%

35. La duración de un bono
 Medida temporal de la vida media de
una inversión.
 Media ponderada del vencimiento de
los flujos de caja de un bono, donde los
valores actuales de dichos flujos actúan
como ponderaciones.
 Media de la volatilidad del precio de
mercado de los bonos como
consecuencia de acambios en la ETTI.

36. D
VA(FC ) x t
VAT
t
t 1
n
 

D= Duración.
FCt=Flujo de caja en el momento t.
VA(FCt)= Valor actual del flujo de caja en el momento t.
VAT= Valor actual o precio de mercado del bono.
n= Número de períodos hasta el vencimiento.
Flujos de caja
0 n
Duración

37. La duración como medida del riesgo de tipo de interés
 
Precio =
-D
(1
r
n
)
x Precio Mercado x Rentabilidad

Rentabilidad del
mercado
Rentabilidad
actual del
mercado
Linea de Duración
Modificada
Cruva Precio-Rentabilidad
Precio actual
del Bono
Precio del
Bono

38. RATING: Indicador de solvencia financiera
AGENCIA MOODY'S AGENCIA STANDARD & POOR'S
Aaa Calidad superior. AAA La mejor calificación.
Aa Alta calidad. AA Calificación alta.
A Superior al grado medio. A Por encima de la media.
Baa De grado medio. BBB Calificación media.
Ba Posee elementos especulativos. BB Por debajo de la media.
B Especulativa. B Especulativa.
Caa Riesgo de impago. CCC Totalmente especulativa
Ca Muy especulativa. Casi seguro impago de
intereses.
C Reservado para deuda subordinada.
C El grado más bajo de calificación. DDD Impago de intereses o de principal.
Fuente: Standard & Poor's y Moody's.