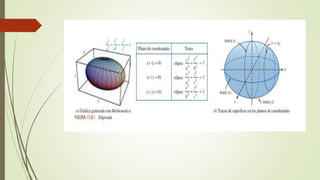
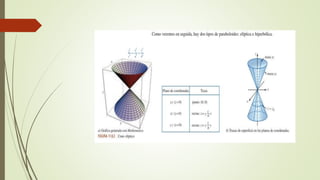
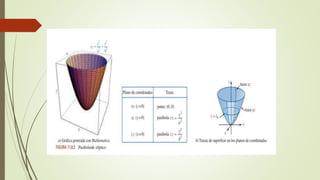
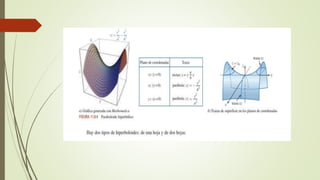
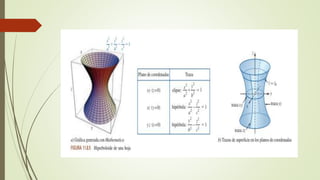
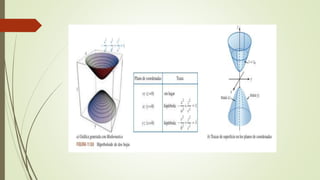
El documento describe conceptos de geometría en el espacio tridimensional, enfocándose en cilindros, esferas y superficies cuadráticas. Se definen cilindros y esferas, presentando sus ecuaciones y ejemplos gráficos, así como introducciones a diversas superficies cuadráticas como el elipsoide y los hiperboloides. Se concluye con ejemplos de ejercicios relacionados con estas superficies y sus ecuaciones.

1. VECTORES Y ESPACIO TRIDIMENSIONAL.
• CILINDROS Y ESFERAS
• SUPERFICIES CUADRATICAS.

2. Introducción
 En el espacio bidimensional la grafica de la ecuación 𝑥2 +𝑦2=1, es una
circunferencia centrada en el origen del plano xy. Sin embargo en el plano
tridimensional es posible interpretar la grafica del conjunto.
[(x,y,z)/ 𝑥2
+ 𝑦2
= 1 , z es arbitraria]

3.  Y+2z=2, esta es la grafica en el espacio bidimensional (en el plano y, z), pero en
el espacio tridimensional la gráfica del conjunto[(x,y,z)/y+2z=2, x arbitraria]

4. CILINDRO
 Usamos el termino cilindro es un sentido mas general que el de un cilindro circular
recto.
 Específicamente, si C es una curva en un plano y L es una recta no paralela al
plano, entonces al conjunto de todos los puntos (x,y,z) generado al mover una
línea que recorra a C paralela a L se denomina cilindro.
 La curva C recibe el nombre de directriz del cilindro.

5.  Una curva C definida por f(x,y)=𝐶1 en el plano x,y y una colección de líneas rojas
llamado bastidor que representa diversas posiciones de una línea generadora que
recorre a C mientras se mueve paralelo al eje z.

6. EJEMPLOS

7. ESFERA
 Definición: Una esfera es el conjunto de todos los puntos P(x,y,z) en el espacio
tridimensional que son equidistantes de un punto fijo llamado centro.
 Si r denota la distancia fija o radio de la esfera, y si el centro es P1(a,b,c)
entones un punto p(x,y,z) esta sobre la esfera si y solo si [d(p1,p)
𝟐
=𝒓𝟐, o
(𝒙 − 𝒂)𝟐
+ (𝒚 − 𝒃)𝟐
+(𝒛 − 𝒄)𝟐
=𝒓𝟐

8. EJEMPLOS
 Grafique 𝑿𝟐 +𝒀𝟐 +𝒁𝟐 = 𝟐𝟓 Identificamos a= 0, b=0 ,C=0 Y 𝒓𝟐=25 , r=5 por
ello la grafica 𝑿𝟐
+𝒀𝟐
+𝒁𝟐
= 𝟐𝟓 es una esfera de radio 5 cuyo centro esta en el
origen.
 grafique(𝑥 − 5)2+(𝑦 − 7)2(𝑧 − 6)2= 9
en este caso identificamos a=5,b=7,c=6 y 𝒓𝟐=𝟑𝟐 advertimos que la gráfica
(𝒙 − 𝟓)𝟐
+(𝒚 − 𝟕)𝟐
(𝒛 − 𝟔)𝟐
= 𝟑𝟐
es una esfera con centro en (5,7,6) y radio 3.

9.  Encuentre una ecuación de la esfera cuyo centro es (4, -3,0) que es tangente al
plano xz.
La distancia perpendicular desde el punto dado hasta el plano xz (y=0), y en
consecuencia el radio de la esfera, es el valor absoluto de la coordenada y, |-3|=3.
Así, una ecuación de la esfera es
(𝑥 − 4)2(𝑦 + 3)2+𝑧2 = 32

10. ejercicios
 𝑦2
+ 𝑥2
=9
 4𝑥2 + 𝑦2=36

11. SUPERFICIES CUÁDRICAS
 Introducción: Las ecuaciones de la esfera dadas anteriormente es solo un caso
particular de la ecuación general de segundo grado en tres variables.𝐴𝑥2
+ 𝐵𝑦2
+
𝐶𝑧2 + 𝐷𝑥𝑦 + 𝐸𝑦𝑧 + 𝐹𝑥𝑧 + 𝐺𝑥 + 𝐻𝑦 + 𝐼𝑧 + 𝐽 = 0 (1)
Donde A,B,C,D,E,F,G,H,I,J son constantes. La grafica de una ecuación de segundo
grado de la forma (1) que describe un conjunto real de puntos se dice que es una
superficie cuádrica. Por ejemplo, tanto el cilindro eliptico
𝑥2
4
+
𝑦2
9
= 1 como el cilindro
parabólico z=𝑦2
son superficies cuádricas. Concluiremos considerando seis
superficies cuádricas adicionales
El elipsoide, el cono elíptico, el paraboloide elíptico, el paraboloide hiperbólico,
el hiperboloide de una hoja y hiperboloide de dos hojas.

12. Elipsoide
 La grafica de cualquier ecuación de la forma.
𝑥2
𝑎2 +
𝑦2
𝑏2 +
𝑧2
𝑐2=1, a>0, b>0, c>0 (2)
Se llama elipsoide, cuando a = b = c, (2) es la ecuación de la esfera centrada en el
origen para |𝑦0|<b, la ecuación
𝑥2
𝑎2 +
𝑧2
𝑐2 = 1 −
𝑦0
2
𝑏2
Representa una familia de elipses ( o circuferencias si a=c) paralelos al plano xz que
se forman rebanando la superficie en planos y=𝑦0. Al elegir a su vez x=𝑥0 y z= 𝑧𝑜
encontramos que las rebanadas son elipses

14. Cono Elíptico
 La grafica de una ecuación de la forma
𝒙𝟐
𝒂𝟐 +
𝒚𝟐
𝒃𝟐 =
𝒛𝟎
𝟐
𝒄𝟐 a>0, b>0, c>0
recibe el nombre de cono elíptico (o circular si el cono a=b) para 𝑧0
arbitraria, planos paralelos al plano xy rebanan la superficie en elipses
cuyas ecuaciones son:
𝒙𝟐
𝒂𝟐 +
𝒚𝟐
𝒃𝟐 =
𝒛𝟎
𝟐
𝒄𝟐

16. Paraboloide elíptico
 La gráfica de una ecuación de la forma:
cz=
𝑥2
𝑎2 +
𝑦2
𝑏2, a>0 , b>0
Se denomina paraboloide elíptico. Advertimos que para C>o, paralelos al plano xy,
cortan la superficie en elipses cuyas ecuaciones son:
𝑥2
𝑎2 +
𝑦2
𝑏2=c𝑧0

18. Paraboloide Hiperbólico
 La grafica de una ecuación de la forma
cz =
𝑦2
𝑎2 +
𝑥2
𝑏2, a>0 , b>0
Se conoce como paraboloide hiperbólica. Advirtiendo que para c>0, los planos z=𝑧0,
paralelos al plano xy corta la superficie en hipérbolas cuya ecuaciones son:
𝑦2
𝑎2 −
𝑥2
𝑏2=c𝑧0

20. Hiperboloide de una Hoja
 La grafica de la ecuación
𝑥2
𝑎2 +
𝑦2
𝑏2 −
𝑧2
𝑐2 = 1 a>0, b>0,c>0
sellama hiperboloide de una hoja. En este caso z=𝑧0, paralelo al plano xy , corta la
superficie en secciones transversales elípticas ( o circulares si a=b). Las ecuaciones de
esta elipse son:
𝑥2
𝑎2 +
𝑦2
𝑏2 = 1+
𝑧0
2
𝑐2

22. Hiperboloide De Dos Hojas
 −
𝑥2
𝑎2 −
𝑦2
𝑏2 +
𝑧2
𝑐2 = 1 a>0, b>0,c>0
se llama apropiadamente hiperboloide de dos hojas para |𝑧0| > 𝑐,
𝑙𝑎 𝑒𝑐𝑢𝑎𝑐𝑖ó𝑛
𝑥2
𝑎2 +
𝑦2
𝑏2=
𝑧0
2
𝑐2−1
describe la curva de intersección elíptica de la superficie
con el plano z=𝑧0