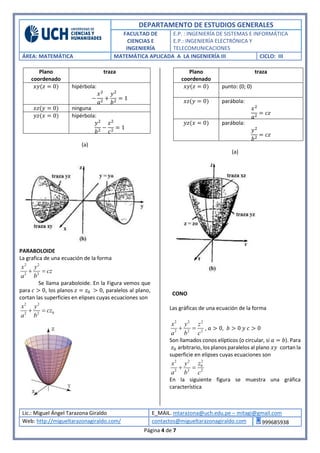
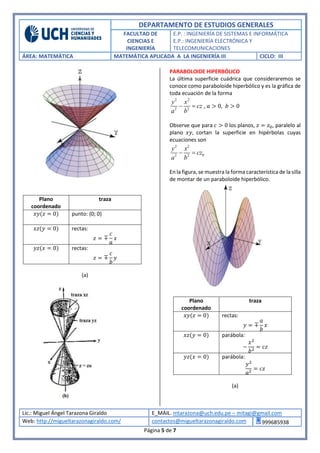
El documento describe diferentes tipos de superficies cuádricas representadas por ecuaciones de segundo grado. Explica que una esfera, elipsoide, hiperboloide de una hoja y cilindro elíptico son ejemplos de superficies cuádricas y analiza las propiedades geométricas de cada una. También analiza cómo estas superficies se intersectan con los planos coordenados.