Este documento describe diferentes tipos de superficies en el espacio tridimensional. Explica que una superficie representa la gráfica de una función de tres variables y puede visualizarse examinando sus intersecciones con planos. Describe superficies cuádricas como esferas, elipsoides e hiperboloides, así como paraboloides y superficies paramétricas.

1. SUPERFICIES
La grafica de una función de tres variables por lo general (x,y,z) representa una superficie
en el espacio de !3. Una función de tres variables asocia cada terna ordenada (x,y,z)
mediante esta relación.
La grafica de la ecuación (x,y,z)=0, es el conjunto de todos los puntos cuyas coordenadas
satisfacen esta ecuación, y esta representación gráfica de la función mencionada
anteriormente, recibe el nombre de superficie en !3.
Los ejemplos más simples de superficies en el espacio de !3 son los planos con ecuación
lineal Ax+By+Cz+D=0.
Para graficar una superficie en el espacio tridimensional, es útil examinar sus intersecciones
con varios planos, como por ejemplo con el plano xy, yz, xz, o también otros planos no tan
comunes como estos tres.
La traza de la superficie en el plano es la intersección de estas dos graficas de superficies.
Por ejemplo si tenemos una esfera que se intercepta con el plano xy, se puede ver
claramente que la traza de esta esfera con respecto al plano es una circunferencia de radio
“r” que dependerá de la ubicación de la esfera respecto al plano. Esto se cumplirá si las dos
superficies se interceptan entre sí pero no son tangentes.
Para visualizar una superficie especifica en el espacio, por lo general basta examinar sus
trazas en los planos coordenados y posiblemente unos cuantos planos paralelos a estos.
Existen distintos tipos de superficies en el espacio, dentro de las cuales se encuentran:
- Superficies Implícitas. F(x,y,z)=0
Cuadráticas
Superficies equipotenciales
- Superficies Explicitas. z=f(x,y);
- Superficies Paramétricas. (x,y,z)=f (u,v)
Las Explicitas se tratan como paramétricas.
Bezier, BSplines, NURBS.
En este trabajo analizaremos solo superficies cuádricas y superficies paramétricas dentro
del espacio !3 y veremos las respectivas graficas de las funciones más usadas.
Cuádricas
Las superficies cuádricas se tratan de primitivas matemáticas que responden a la ecuación:
Ax2+By2+Cz2+Dxy+Exz+Fyz+Gx+Hy+Iz+J=0
Dependiendo de los valores de los coeficientes generamos: esferas, elipsoides, toros,
hiperboloides, etc.

2. Esta ecuación de la representación de superficies cuádricas está referida a ejes que no son
de simetría (ejes arbitrarios), donde al menos uno de los seis primeros coeficientes es no
nulo. Esta ecuación puede reducirse a una en la cual no figuren los productos entre las
variables. Mediante una rotación adecuada de coordenadas, pueden eliminarse luego los
términos que contienen las primeras potencias de las nuevas variables mediante una
translación. Se llegara entonces a las ecuación más simple para dicha cuádrica; esta
ecuación es la ecuación canónica de la cuádrica.
Ax2+By2+Cz2+Dx+Ey+Fz+G=0
Las superficies cuádricas se pueden clasificar en cuádricas no degeneradas que son
cinco: tres de ellas poseen centro de simetría (elipsoide, hiperboloide de una hoja y de dos
hojas) y las dos restantes no poseen centro de simetría (paraboloide elíptico e hiperbólico
o silla de montar).
Las cuádricas degeneradas son conos, planos dobles y cilindros.
Cualquier superficie ubicada arbitrariamente respecto de los ejes x,y,z; es posible centrarla
en el origen (si tiene centro) respecto a un nuevo sistema de ejes coordenados x',y',z'
mediante adecuadas translaciones y rotaciones del sistema x,y,z.
Dada la ecuación general de las cuádricas:
a11x2+a22y2+a33z2+a12xy+a13xz+a23yz+a14x+a24y+a34z+a44=0
y a partir de los coeficientes aij, definimos una serie de parámetros que los llamaremos
invariantes, ya que los mismos no se modifican con las operaciones roto - translatorias que
llevan x,y,z a x',y',z' estas invariantes son:
S= a11+a22+a33 T= a11a22+a11a33+a22a33+a122+a132+a232
Siendo E = menor principal 0, de mayor rango.
Los números , , S, T y E, calculables a partir de los aij = aji permiten junto con el rango de
la matriz 4x4, reconocer cual es la cuádrica que corresponde a una ecuación dada, según
se indica en el cuadro de la última página:
Cuádricas no degeneradas
Entre las cuadráticas no degeneradas están las del tipo:
- Mx2+Ny2+Pz2 = R2 con R>0 {centradas}
- Mx2+Ny2 = Sz {no centradas}
Dentro de superficies cuádricas centradas no degeneradas se encuentran, esferas,
elipsoides, hiperboloides de una y de dos hojas y entre las no centradas y no degeneradas
se encuentran el paraboloide elíptico y el paraboloide hiperbólico. Dentro del estudio de las
superficies cuádricas que estudiaremos se analizarán en su forma canónica.
No degeneradas centradas
La esfera
Si la ecuación general de las cuádricas se reduce a la forma

3. x2+y2+z2 = R2
Se obtiene una superficie esférica con centro en el origen de coordenadas y radio R. Si en
cambio la esfera está centrada en el punto (a,b,c) la ecuación se expresa:
(x-a)2+(y-b)2+(z-c)2 = R2
Elipsoide:
Si la ecuación general de las cuádricas, los coeficientes son tales que puede ser expresada
como:
Entonces la ecuación representa un elipsoide centrado en el origen, simétrico con respecto
a cada uno de los tres planos y tiene intersecciones en (±a,o,o),(0,±b,0),(0,0,±c). Al igual
que en la esfera, el elipsoide puede estar centrado en cualquier otro punto del espacio
haciendo x = x-x0, y = y-y0, z = z-z0.
Para representar gráficamente la ecuación de un elipsoide, se encuentran las trazas con
planos paralelos a los coordenados. Estas curvas van formando una red que soporta a la
superficie.
Tomando planos horizontales paralelos al xy y a una altura k, de ecuación z=k, la
intersección del elipsoide con este plano es que corresponde a una elipse siempre que:
En forma similar se pueden estudiar las intersecciones con los planos paralelos a los planos
coordenados xz y yz.
Hiperboloide de una hoja:
Su ecuación canónica es
Las intersecciones con diferentes planos se detallan a continuación:
Con z=k: produce elipses con semidiámetros crecientes a medida que k aumenta partiendo
de 0.

4. Si k = 0, se obtiene la elipse más pequeña con semidiámetros a y b, que representa la
garganta del hiperboloide.
Con x = k e y = k, las intersecciones son hipérbolas. Si a = b corresponde a un hiperboloide
circular de una hoja.
Hiperboloide de dos hojas:
Su ecuación canónica es
Las intersecciones con planos paralelos a los planos coordenados son con z = k:
corresponden a elipses con semidiámetro crecientes siempre que:, si k = c, la elipse se
reduce a un punto, significa que entre los planos z = -c y z = c no hay puntos de la superficie.
si a = b corresponde a un hiperboloide circular de dos hojas.
Con x =k e y =k las intersecciones son hipérbolas.
No degeneradas no centradas
Paraboloide: si en la ecuación general de las cuadráticas, faltan los términos rectangulares
o cruzados y además no está presente el término de segundo grado correspondiente a una
de las variables, la superficie recibe el nombre de paraboloide. Los paraboloides pueden
ser de dos tipos: elípticos (circulares) o hiperbólicos.
Paraboloide elíptico:
Responde a la ecuación
Para hallar su gráfica se encuentran las intersecciones con los planos z =k, si c >0 la
ecuación anterior representa elipses con semidiámetros crecientes a medida que
aumenta k (k >0). En el caso en que k =0 se obtiene un punto (el vértice del paraboloide).
Si c >o el paraboloide se abre hacia arriba, si c< 0 el paraboloide se abre hacia abajo. Si a
=b se obtiene un paraboloide circular.
Cortando con planos x=k, la ecuación resultante representa parábolas de eje z, con vértices
que se desplazan en la dirección positiva del eje z a medida que k aumenta en valor
absoluto.
Cortando con planos y=k, que da parábolas de eje z, con vértices en ascenso a medida
que k aumenta.
Paraboloide hiperbólico:
Su ecuación es:
Si suponemos que c >0, las intersecciones son:
-Con los planos z =k, hipérbolas que cambian de eje con el signo de k.
-Si k = 0 se reduce a un par de rectas
-Con x =k: parábolas de eje con ramas descendentes y vértices en ascenso.

5. -Con y =k: quedan determinadas parábolas de eje z con ramas ascendentes y vértices en
descenso. La superficie tiene la forma de una silla de montar.
Así el origen parece un máximo local desde una dirección, pero un mínimo local desde una
dirección distinta. Tal punto de una superficie se llama punto silla.
Cuádricas degeneradas
Entre las cuadráticas degeneradas están las del tipo:
- Mx2+Ny2+Pz2 = R2; R"0 {centradas}
- Mx2+Ny2 = Sz {no centradas}
Dentro de superficies cuádricas centradas degeneradas se encuentran conos, cilindro
elíptico, cilindro hiperbólico, planos dobles. Y entre las no centradas y degeneradas se
encuentra el cilindro parabólico.
Degeneradas centradas
Cono:
Su ecuación canónica es:
Las intersecciones dan:
-Con z =k, son elipses con semidiámetros crecientes y que se reducen a un punto
cuando k =0.
-Con x =k e y =k las intersecciones son hipérbolas de eje vertical.
Si a =b las trazas con los planos paralelos al plano xy son circunferencias, por lo tanto sería
un cono circular.
Cilindro elíptico:
Su ecuación canónica es:
Si z =k, las intersecciones son elipses con semidiámetros constantes, si a =b será un cilindro
circular.
Con x =k e y =k las intersecciones son líneas rectas separadas a igual distancia del centro
del cilindro.
Cilindro hiperbólico:
Su ecuación canónica es:
Si z =k las intersecciones son hipérbolas constantes.
Degeneradas no centradas
Cilindro parabólico:
Su ecuación canónica es: Mx2 = Sz (ó también Ny2 = Sz )

6. Las intersecciones dan:
-Con y =k: Mx2 = Sz, son parábolas crecientes si M y Z son mayores que 0.
Sea un vector " y P0 un punto dado, el conjunto de todos los puntos para los cuales
(P0P) y son ortogonales define al plano que pasa por P0 y tiene a como vector normal.
Si P0(x0, y0, z0) es un punto de un plano y = (a, b, c) es un vector normal al plano,
entonces una ecuación del plano es:
a(x - x0 ) + b (y - y0 ) + c (z - z0 ) = 0
El producto escalar entre el vector normal al plano y un vector del mismo es igual a cero:
( P) = (x - x0, y - y0, z - z0)
· = a (x - x0) + b (y - y0) + c (z - z0 ) = 0
Si [ax + by + cz +d = 0] es la ecuación de un plano = (a, b, c) es un vector normal al plano.
Es un ejemplo de un plano en el espacio.
Superficies paramétricas
Una superficie paramétrica es la imagen de una función o transformación r definida en una
región R de un plano uv y que tiene valores en el espacio xyz. La imagen bajo r en cada
punto (u,v) en R es el punto del espacio xyz con vector de posición.
r(u,v)= x(u,v), y(u,v), z(u,v)
Dado que una superficie paramétrica es una imagen de una transformación en el espacio,
es posible por lo tanto tomar coordenadas cilíndricas y esféricas, para expresar la superficie
con otros parámetros distintos a los rectangulares.
Algunos ejemplos de superficies paramétricas:
Cilindro circular
[cos u, sin u, v]

7. Cono circular
[v cos u, v sin u, v]
u cosh v, u sinh v, u2

8. [(u - sin u)cos v,(1 - cos u)sin v, u]
[u2 + vu, u + vu2, v]
(superficie reglada)

9. [eu + veu, e-u - ve-u, u + v]
(desarrollable tangencial)
(desarrollable tangencial)
Trompeta de Gabriel

10. Toro
(2 + cos u)cos v,(2 + cos u)sin v, sin u
Tampa espiral
u cos v, u sin v, 2v

11. SUPERFICIES CUADRICAS
1. Ecuaciones paramétricas de una esfera
x=rsin(u)cos(v)
y=rsin(u)sin(v)
z=rcos(v)
x=3sin(u)cos(v); y=3sin(u)sin(v); z=3cos(v)
2. Ecuaciones paramétricas de un elipsoide
x= asin(u)cos(v)
y=bsin(u)sin(v)
z=ccos(v)
x=4sin(u)cos(v); y=4sin(u)sin(v); z=2cos(v);

12. 3. Ecuaciones paramétricas de un hiperboloide elíptico (de una hoja)
x=acosh(u)cos(v)
y=bcosh(u)sin(v)
z=sinh(u)
x=4cosh(u)cos(v); y=3cosh(u)sin(v); z=7sinh(u)
4. Ecuaciones paramétricas de un hiperboloide hiperbólico (de dos hojas)
x=asinh(u)cos(v)
y=bsinh(u)sin(v)
z=ccosh(u)
x= 4sinh(u)cos(v), y=3sinh(u)sin(v), z= 7cosh(u)

13. 5. Ecuaciones paramétricas de un paraboloide elíptico
x=aucos(v)
y=busin(v)
z=cu
x= 4ucos(v), y=3usin(v); z=7u
6. Ecuaciones paramétricas de un paraboloide hiperbólico
x=aucosh(v)
y=busin(v)
z= cu
x=3ucosh(v); y=2usen(v); z=5 u

14. 7. Ecuaciones paramétricas de un cono
x=avcos(u)
y=bvsin(u)
z=cv
x=2vcos(u); y=3vsin(u); z=5v
8. Ecuaciones paramétricas de un cilindro elíptico
x=acos(u)
y=bsin(u)
z=v
x=3cos(u); y=2sin(u); 5z=v;

15. 9. Ecuaciones paramétricas de un cilindro hiperbólico
x=acosh(u)
y=bsinh(u)
z=v
x=4cosh(u); y=3sinh(u); z=v
10. Ecuaciones paramétricas de un cilindro parabólico
x=u
y=1/(2p)*u
z=v
x=u; y=-4u; z=v

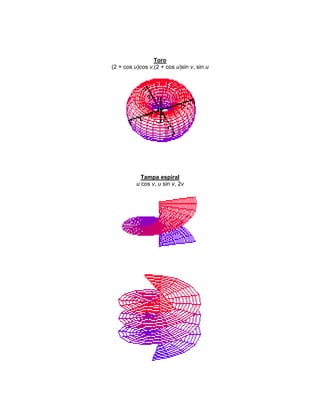
16. 11. Ecuaciones paramétricas de una superficie cilíndrica
x(t) = (2 + cos(t)) cos(')
y(t') = (2 + cos(t)) sen(')
z(t) = t
t E [0; 2¼];
12. Ecuaciones paramétricas de la pseudoesfera
x=r*sen(t)*cos(s)
y=r*sent(t)*sen(s)
z=r*(cos(t)+log(tg(t/2)))

17. 13. Ecuaciones paramétricas de un Astroide
14. Ecuaciones paramétricas de una cubeta de huevos

18. 15. Ecuaciones paramétricas de bonete cruzado
16. Ecuaciones paramétricas de un serpentin

19. 17. Ecuaciones paramétricas de un whitney
http://www.mathcurve.com/surfaces/superficies.shtml