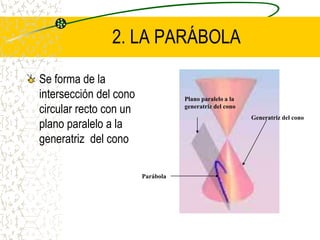
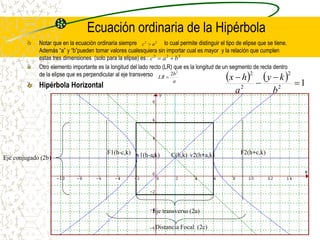
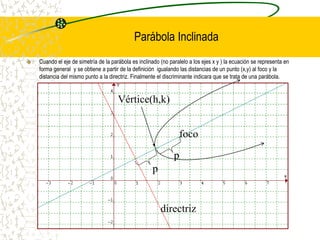
El documento describe las cuatro secciones cónicas principales (circunferencia, parábola, elipse e hipérbola) que se generan al interceptar un cono circular recto con un plano. Explica cómo cada una se forma dependiendo de la posición del plano, y provee las ecuaciones generales y particulares que definen cada curva cónica.

1. SECCIONES CONICAS
INTRODUCCIÓN

2. DEFINICIÓN
Curvas o lugares
geométricos que se
generan al interceptar un
plano con un cono
circular recto.
Generatriz del
cono

3. 1. LA CIRCUNFERENCIA
Se forma de la
intersección del cono
circular recto con un
plano horizontal, paralelo
a la base del cono
Plano paralelo a la
base
Circunferencia
Base del cono

4. 2. LA PARÁBOLA
Se forma de la
intersección del cono
circular recto con un
plano paralelo a la
generatriz del cono
Generatriz del cono
Parábola
Plano paralelo a la
generatriz del cono

5. 3. LA ELIPSE
Se forma de la
intersección del cono
circular recto con un
plano oblicuo a la base
del cono
Plano oblicuo a la
base
Base del cono
Elipse

6. 4.LA HIPÉRBOLA
Se forma de la
intersección del cono
circular recto con un
plano vertical,
perpendicular a la base
del cono
Notar que son dos ramas con tendencia
parabólica
Plano perpendicular
a la base
Hipérbola

7. Identificación de las cónicas
Ecuación de segundo grado
Una ecuación de segundo grado con dos variables es una
ecuación de la forma:
Donde A,B,C,D,E,F son constantes arbitrarias no todas iguales
a cero.
El conjunto de pares ordenados (x,y) del plano que satisfacen
la ecuación anterior se llama sección cónica.
De la ecuación general de segundo grado puede obtenerse ,
en particular las ecuaciones correspondientes a las
cónicas.
0
)
,
( 2
2






 F
Ey
Dx
Cy
Bxy
Ax
y
x
f

8. 1.Forma general de la circunferencia
De la ecuación:
Si B=0 y A=C se dice que la cónica es una circunferencia.
Obteniendo así la ecuación general de la circunferencia
Dividiendo entre A a ambos lados se puede generalizar la misma
ecuación con coeficientes unitarios en los términos cuadráticos
de X y Y
0
)
,
( 2
2






 F
Ey
Dx
Cy
Bxy
Ax
y
x
f
0
2
2




 F
Ey
Dx
Ay
Ax
0
2
2




 F
Ey
Dx
y
x

9. Ecuación Ordinaria de la Circunferencia
Definición:Es el lugar geométrico (conjunto) de todos los puntos del plano que
estan a una distancia dada (radio) de un punto dado(centro), tal que esa
distancia es constante.
Consideremos el puntoP(x,y) del
plano , y el punto C(h,k),centro que
no pertenece al lugar geométrico.
Usando teorema de Pitágoras y el
concepto de distancia se tiene en la
figura:
|CP|2=|BC|2+|PB|2
R 2=(x-h)2+(y-k)2
h
k
(x,y)
y
x
(h,k)
R Y-k
X-h

10. Ecuación ordinaria de una circunferencia de radio “r” y centro (h,k)
Si la circunferencia esta centrada (h,k)=(0,0) entonces:
A partir de la ecuación general, se llega a determinar los elementos principales
mediante un complemento de cuadrados:
Agrupando:
    2
2
2
r
k
y
h
x 



2
2
2
r
y
x 

0
2
2




 F
Ey
Dx
y
x
    F
Ey
y
Dx
x 



 2
2
4
4
4
4
2
2
2
2
2
2 E
D
F
E
Ey
y
D
Dx
x 































 

















4
4
2
2
2
2
2
2
F
E
D
E
y
D
x

11. De la ecuación anterior se deduce que para :
Los elementos intrinsicos son:
Observar: si r 2 < 0 no hay lugar geométrico
si r 2 =0 el lugar geometrico es un punto
si r 2 > 0 el lugar geometrico es una circunferencia de radio r
Ejemplos:
Determine la ecuación ordinaria y general de una circunferencia de radio 5 y centro en (-3,4).
Sustituyendo en la ecuación tenemos:
Desarrollando los binomios y simplificando
Se obtiiene la ecación general:
    2
2
2
r
k
y
h
x 



4
4
,
2
,
2
2
2
2 F
E
D
r
E
k
D
h







    2
2
2
r
k
y
h
x 



    2
2
2
5
4
3 


 y
x
0
8
6
2
2



 y
x
y
x

12. Encuentre el centro y radio de la circunferencia
Agrupando términos y factorando:
0
25
20
12
4
4 2
2




 x
x
y
x
    4
25
5
4
4
3
4
4 2
2



 y
y
x
x
4
59
2
5
2
3
2
2















 y
x

13. Representa la ecuación de una circunferencia expresada en forma general, puesto
que se ha obtenido de la ecuación general de segundo grado con dos variables.
Ordenando términos en relación a las variables: 2x2 -3x+ 2 y2+4y-5=0
Agrupando términos: (2x2 -3x )+ ( 2 y2+4y)=5
Dividiendo ambos miembros entre 2:
Completando cuadrados:
0
5
4
3
2
2 2
2




 y
x
y
x
La ecuación
  5
2
2
2
3
2 2
2









 y
y
x
x
 
2 2
3 5
2
2 2
x x y y
 
   
 
 
 
2 2
3 9 5 9
2 1 1
2 16 2 16
x x y y
 
       
 
 
 
2
2
3 65 3 65
1 Circunferencia de Centro C , 1 y radio r=
4 16 4 16
x y
   
    
   
   

14. Uso del discriminante de la ecuación general
cuadrática
A partir de la ecuación general, se le llama discriminante de la
ecuación a la expresión: D=B2- 4AC
Si B2- 4AC=0. Se dice que la cónica es una Parábola.
Si B2- 4AC<0. Se dice que la cónica es una Elipse.
Si B2- 4AC>0. Se dice que la cónica es una Hipérbola.
Ejemplo: identificar el tipo de cónica mediante el uso del
discriminante
0
5
2
3
2
3
3 2
2





 y
x
y
xy
x
     Elipse
es
0
es
como
,
15
2
3
4
3
4
2
2






 AC
B
0
3
2
3
2
6
3 2
2





 y
x
y
xy
x
     Hipérbola
es
0
es
como
,
12
2
3
4
6
4
2
2




 AC
B

15. Parábola. Ecuación Ordinaria.
Definición:Es el lugar geométrico (conjunto) de todos los puntos del plano que
equidistan de un punto y una recta dados de tal manera que el punto no pertenece a
la recta.
La recta y el punto dados estan sobre el plano y se llaman directiz y foco,
respectivamente.
Consideremos el puntoP(x,y) del
plano , y el punto V(h,k),Vertice que
pertenece al lugar geométrico.F un
punto que pertenece a un eje de
simetria de la parabola,ubicado a p
unidades del V y D la recta directiz
externa a la parábola ,y
perpendicular al eje de simetria y
tambien ubicada a p unidades del v,
entonces:
|FP|=|DP|
F(p,0)
P(x,y)
D
d1
d2 d1=d2

16. Planteando la igualdad de distancias, entre puntos y de un punto a una recta:
Elevando al cuadrado a ambos lados:
Despejando el cuadrado de y:
Siendo esta la ecuación de una parábola abierta a la derecha con vertice en el origen y foco (p,0)
Si se abriera hacia las x negativas la ecuación es:
Si el vertice no es (0,0) , sino que (h,k) y si se abriera es sentido vertical las ecuaciones solo se
desplazan en x y y en h,k respectivamente y los términos cuadráticos cambian. Estos casos
particulares se presentan a contnuación.
   2
2
2
p
x
y
p
x 



   2
2
2
p
x
y
p
x 



px
y 4
2

px
y 4
2



17. Ecuaciones Ordinarias de la Parábola
Parábola Horizontal (abierta hacia la derecha)    
h
x
p
k
y 

 4
2
Directriz x=h-p
Foco(h+p,k)
Vértice(h,k)
p
p

18. Ecuaciones Ordinarias de la Parábola
Parábola Horizontal (abierta hacia la izquierda)    
h
x
p
k
y 


 4
2
Directriz x=h+p
Foco(h-p,k)
Vértice(h,k)
p
p

19. Ecuaciones Ordinarias de la Parábola
Parábola Vertical (abierta hacia arriba)    
k
y
p
h
x 

 4
2
Directriz y=k-p
Foco(h,k+p)
Vértice(h,k)
p
p

20. Ecuaciones Ordinarias de la Parábola
Parábola Vertical (abierta hacia abajo)    
k
y
p
h
x 


 4
2
Directriz y=k+p
Foco(h,k-p)
Vértice(h,k)
p
p

21. Ecuación Ordinaria de la Elipse
Definición: Es el lugar geométrico de los puntos de un plano tales que la suma de las distancias
de dos puntos fijos llamados focos a un punto p(x,y) es constante .
Una elipse tiene dos ejes de simetría que son perpendiculares entre si; el eje mas largo se llama
“eje mayor” y el mas corto “eje menor” , el punto de intersección de los ejes se llama “centro de la
elipse”.También se tienen dos puntos fijos internos a la elipse y situados sobre el eje mayor a “c”
unidades del centro de coordenadas (h,k). La elipse tiene 2 vértices los cuales son los 2 puntos
donde el eje mayor intercepta la curva.
La longitud del eje mayor es 2a unidades, mientras que la del eje menor es 2b unidades.
Observar la gráfica de una elipse con sus elementos principales.
|F1P|+|F2P|=2a
al elevar al cuadrado y completar cuadrados
se genera una ecuación ordinaria que involucra
a todos sus elementos:
F1(h-c,k) F2(h+c,k)
P(x,y)
d1 d2
a a
b c
c
b
V(h,k)
 
     
    a
k
y
c
h
x
k
y
c
h
x 2
2
2
2
2










    1
2
2
2
2




b
k
y
a
h
x

22. Ecuación ordinaria de la Elipse
Notar que en la ecuación ordinaria siempre lo cual permite distinguir el tipo de elipse que se tiene.
Además siempre c < a y la relación que cumplen estas tres dimensiones (solo para la elipse) es :
Otro elemento importante es la longitud del lado recto (LR) que es la longitud de un segmento de recta dentro
de la elipse que es perpendicular al eje mayor
Elipse Horizontal
2
2
b
a 
2
2
2
c
b
a 

C(h,k) F2(h+c,k)
F1(h-c,k) v2(h+a,k)
v1(h-a,k) Eje menor (2b)
Eje mayor (2a)
a
b
LR
2
2

    1
2
2
2
2




b
k
y
a
h
x

23. Ecuación ordinaria de la Elipse
Elipse Vertical
C(h,k)
F2(h,k-c)
F1(h,k+c)
v2(h,k-a)
v1(h,k+a)
Eje menor (2b)
Eje mayor (2a)
    1
2
2
2
2




b
h
x
a
k
y

24. Ecuación Ordinaria de la Hipérbola
Definición: Es el lugar geométrico de los puntos de un plano, tales que el valor absoluto de la
diferencia de las distancias desde dos puntos fijos llamados focos a un punto p(x,y) es constante
.
La Hipérbola tiene dos ejes de simetría, perpendiculares entre si. El eje que intercepta a la
hipérbola se llama “eje transverso”. y el perpendicular “eje conjugado” , el punto de intersección
de los ejes se llama “centro de la hipérbola”.
Los puntos donde el eje transverso corta a la Hipérbola se llama “Vértice de la Hipérbola”. Cada
Hipérbola tiene dos “Asíntotas”, que son rectas que se interceptan en el centro de la hipérbola.
Los focos son los dos puntos fijos internos a la Hipérbola y situados sobre el eje transverso a “c”
unidades del centro de coordenadas (h,k). La Hipérbola tiene 2 vértices los cuales son los 2
puntos donde el eje transverso intercepta la curva.
|F1P| - |F2P|=2a
al elevar al cuadrado y completar cuadrados
se genera una ecuación ordinaria que involucra
a todos sus elementos:
F1(h-c,k) F2(h+c,k)
P(x,y)
d1 d2
2b
2a
2c
V(h,k)
 
     
    a
k
y
c
h
x
k
y
c
h
x 2
2
2
2
2










    1
2
2
2
2




b
k
y
a
h
x

25. Ecuación ordinaria de la Hipérbola
Notar que en la ecuación ordinaria siempre lo cual permite distinguir el tipo de elipse que se tiene.
Además “a” y “b”pueden tomar valores cualesquiera sin importar cual es mayor y la relación que cumplen
estas tres dimensiones (solo para la elipse) es :
Otro elemento importante es la longitud del lado recto (LR) que es la longitud de un segmento de recta dentro
de la elipse que es perpendicular al eje transverso
Hipérbola Horizontal
2
2
a
c 
2
2
2
b
a
c 

C(h,k) F2(h+c,k)
F1(h-c,k) v2(h+a,k)
v1(h-a,k)
Eje conjugado (2b)
Eje transverso (2a)
a
b
LR
2
2
     1
2
2
2
2




b
k
y
a
h
x
Distancia Focal (2c)

26. Ecuación ordinaria de la Hipérbola
Hipérbola Vertical
C(h,k)
F2(h,k-c)
F1(h,k+c)
v2(h,k-a)
v1(h,k+a)
Eje conjugado (2b)
Eje transverso
(2a)
    1
2
2
2
2




b
h
x
a
k
y
Distancia focal
(2c)

27. Parábola Inclinada
Cuando el eje de simetría de la parábola es inclinado (no paralelo a los ejes x y ) la ecuación se representa en
forma general y se obtiene a partir de la definición igualando las distancias de un punto (x,y) al foco y la
distancia del mismo punto a la directriz. Finalmente el discriminante indicara que se trata de una parábola.
p
p
Vértice(h,k)
foco
directriz

28. Elipse Inclinada
Cuando los ejes de simetría de la elipse son inclinado (no paralelo a los ejes x y ) la ecuación se representa en
forma general y se obtiene a partir de la definición sumando las distancias de un punto (x,y) a los focos .
Finalmente el discriminante indicara que se trata de una Elipse.
c
c
centro(h,k)
focos
directriz
Vértices
a
a

29. Hipérbola Inclinada
Cuando los ejes de simetría de la Hipérbola son inclinado (no paralelo a los ejes x y) la ecuación se representa
en forma general y se obtiene a partir de la definición restando las distancias de un punto (x,y) a los focos .
Finalmente el discriminante indicara que se trata de una Hipérbola.
a
a
centro(h,k)
Vértices
asíntotas
focos
c
c