ORGANIZACIÓN-ESTADISTICA

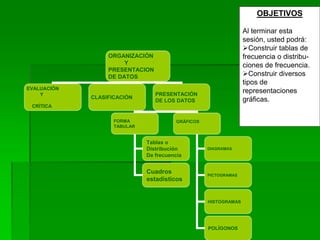
1. OBJETIVOS
Al terminar esta
sesión, usted podrá:
Construir tablas de
frecuencia o distribu-
ciones de frecuencia.
Construir diversos
tipos de
representaciones
gráficas.
ORGANIZACIÓN
Y
PRESENTACION
DE DATOS
EVALUACIÓN
Y
CRÍTICA
CLASIFICACIÓN
PRESENTACIÓN
DE LOS DATOS
FORMA
TABULAR
GRÁFICOS
DIAGRAMAS
PICTOGRAMAS
HISTOGRAMAS
POLÍGONOS
Tablas o
Distribución
De frecuencia
Cuadros
estadísticos

2. ORGANIZACIÓN Y
PRESENTACIÓN DE DATOS
 POBLACIÓN
 o MUESTRA DATOS
SUJETO
INVESTI-
GADOR
U1 ,U2 , … , Un X 1, X2 ,…, Xn
OBJETIVO
VARIABLE X

3. EVALUACIÓN Y CRITICA.-
Consiste en inspeccionar la validez y
confiabilidad de los datos, para corregir los
errores y omisiones de acuerdo a ciertas reglas
fijas. A partir de datos incorrectos no se pueden
obtener buenos resultados.
CLASIFICACIÓN.-
Consiste en establecer las clases o categorías
o modalidades de las variables.

4. PRESENTACIÓN DE LOS DATOS.-
Consiste en tener la información estadística
organizada para proceder al análisis e
interpretación de los resultados.
Hay dos formas :
1.- Forma tabular, como: las distribuciones de
frecuencia y los cuadros estadísticos.
2.- Gráficas, como: diagrama de barras,
diagrama de sectores, pictogramas, diagrama
de escalera, histograma, polígono de
frecuencias, polígono de frecuencias
acumuladas, diagrama de tallos y hojas, etc.

5. DISTRIBUCIONES O TABLAS DE FRECUENCIAS.-
Son tablas que recogen de un modo sistemático los
datos de una variable.
Sea X la variable
x1 ,x2 , x3 , … , xn son los datos de la variable.
Elementos de la tabla :
1.-Clases o categorías o modalidades de la variable.
Representar : Xi i= 1,2, …, k , donde k ≦n
2.-Frecuencia absoluta o repetición.-
Indica las veces que se repite un dato
en cada clase.
Representar : f i i= 1,2,…,k

6. 3.- Frecuencia relativa.-
Es el cociente entre la frecuencia absoluta y el total de
observaciones.
Representar : hi i : 1,2 ,…, k
hi = fi / n
4.- Frecuencia relativa porcentual.-
Representar : hi % = hi x 100
5.- Frecuencia absoluta acumulada
i
representar : Fi = ∑ f j i=1,2,…, k
j=1
6.- Frecuencia relativa acumulada.-
Representar : Hi = Fi / n i=1,2,3,…,k
7.- Frecuencia relativa acumulada porcentual.-
representar : Hi % = Hi x 100

7. DISTRIBUCION DE FRECUENCIAS
Clase
Xi
conteo fi hi hi % Fi Hi Hi %
x1 //// f1 h1 h1 x100 F1 H1 H1x100
x2 /// f2 h2 h2 x100 F2 H2 H2x100
x3 // f3 h3 h3 x100 F3 H3 H3x100
…
xK / fK hK hK x100 FK HK Hkx100
total n 1 100

8. Ejemplo 1.- Deseamos conocer el % de
hombres y mujeres que llevan el curso
de estadística, de una escuela
profesional. Cuyos datos son:
m, m, m, m, m, h, h, h, h, h, h, h, h, h, h,
h, h.
a)Construir una tabla de frecuencias e
interpretar.
b)Elaborar gráficas.
Solución:
a)Variable X: sexo
Categorias o clases: m, h

9. TABLA N° 01
DISTRIBUCION DE ESTUDIANTES DEL
CURSO DE ESTADISTICA POR SEXO
SEXO CONTEO fi hi hi % Өi =360° x hi
M
H
/////
////////////
5
12
5/17 = 0,29
12/17 = 0,71
29
71
104,4
255,6
Total 17 1,00 100 360

12. Ejemplo 2.- Los siguientes datos recopilados
corresponden al número de hijos que poseen
30 familias, tomadas del distrito de Pueblo
Libre.
2 3 3 0 3 0 1 2 3 2 4 2 4 1 4 3 1 3 4
2 2 4 3 0 1 1 4 2 3 0
a)¿Qué constituye la población ?
b) ¿Cuál es la unidad estadística ?
C)¿Qué constituye la muestra ?
d) ¿ Cuál es la variable en estudio ?
e) Construir la tabla de frecuencias e
interpretar.
f) Graficar e interpretar.

13. a) Todas las familias del distrito de
Pueblo Libre.
b) Cada familia.
c) n = 30 familias.
d) X : número de hijos por familia.
e) Construcción de la tabla
Valores distintos de la variable X
Y = 0 , 1 , 2 , 3 , 4

14. Yi conteo fi hi hi % Fi Hi Hi %
y1 = 0 //// f1 = 4 0,13 13 4 0,13 13
y2 = 1 ///// f2 = 5 0,17 17 9 0,30 30
y3 = 2 /////// f3 = 7 0,23 23 16 0,53 53
y4 = 3 //////// f4 = 8 0,27 27 24 0,80 80
y5 = 4 ////// f5 = 6 0,20 20 30 1,00 100
Total
30 1,00 100

15. DISTRIBUCIÓN DE FRECUENCIAS AGRUPADOS
EN INTERVALOS
Cuando en la población o muestra los datos son
distintos o existen muchos valores diferentes y por lo
tanto mucha variabilidad se recomienda, aún a costa
de perder información, agrupar los datos en
intervalos.
Sea X la variable
x1 ,x2 , x3 , … , xn
Elementos de la tabla
1.- Intervalos de clase
1.1.- Rango o recorrido
representar : R
R = máx de X - mín de X

16. 1.2.- Número de intervalos de clase.
representar : K
-Se buscará el número de intervalos que
equilibre dos aspectos : que evite el detalle
innecesario, pero que no conduzca a la
pérdida total de información.
-A modo orientativo, consiste en dividir el
rango R en un número conveniente de
intervalos de clase, generalmente del mismo
tamaño o de diferente tamaño.
-Formas de determinar el número de
intervalos :

17. a) 5  K  20 dependiente del tamaño de datos
b) K = n
c) Fórmula de H.A. Sturges K = 1 + (10/3) log (n)
1.3.- Longitud o amplitud de los
intervalos de clase
representar : c
Tenemos dos casos :
a) amplitud del mismo tamaño
c = R / K
- Si c es un valor exacto, todos los intervalos de
clase deben tener la misma longitud, con la posible
excepción del último intervalo, que lo cerramos para
que tome el dato último.
- Si c es un valor periódico, será necesario ampliar el
recorrido, se aproxima por exceso de manera que
cubra todo el rango, es decir
c  c’ / c  c’ tal que c’ K = R’  R

18. b)amplitud variable, se produce cuando hay
poca información en los intervalos de clase,
se une intervalos.
1.4.- Elección de intervalos
Intervalos semiabiertos por la derecha
 Y’i-1 - Y’i ) i = 1,2,…, k
2.- Marcas de clase
representar : Yi i = 1,2,…,k
Yi = ( Y’i-1 + Y’i ) / 2
es el punto medio del intervalo de clase.

19. Ejemplo 3.- Los siguientes
datos son las edades de 20
personas elegidos al azar de
un grupo de 1000 personas
de una determinada ciudad.
Cuyos datos son:
2, 6, 7, 9, 10, 12, 12, 14, 15,
16, 16, 18, 19, 20, 21, 22, 25,
27, 29, 32.

20. a)¿Qué constituye la población?
b) ¿Qué constituye la unidad
estadística ?
c)¿Qué constituye la muestra?
d) ¿Cuál es la variable ?
e)Organice y presente los datos
en una tabla de frecuencias.
f)Interprete: f4 , F3 , h2 , H5
g)Grafique cada una de las
frecuencias.

21. a) Población N=1000 personas
b) Unidad estadística: cada persona.
c) Muestra n= 20 personas.
d) Variable X : edad de la personas.
e) Rango=R= max. X – min. X =32-2=30
Número de intervalos de clase: K
Método de Sturges K=1+(10/3)log 20=5
Longitud de los intervalos de clase: C
C=R/K = 30/5 = 6

22. [Yj-1- Yj ) Yi fi hi hi % Fi Hi Hi %
[2 – 8 ) 5 3 0,15 15 3 0,15 15
[8 – 14 ) 11 4 0,20 20 7 0,35 35
[14- 20) 17 6 0,30 30 13 0,65 65
[20- 26 ) 23 4 0,20 20 17 0,85 85
[26-32 ] 29 3 0,15 15 20 1,00 100
Total 20 1,00 100

24. REPRESENTACION GRAFICA DE DATOS
ESTADISTICOS
- Hay un proverbio chino que dice:
“una imagen vale más que mil palabras”
- Los gráficos trasmiten información de
modo más expresivo.
- Las representaciones gráficas nos
permite entender de manera fácil,
rápida, directa, comprensible el tema
del que se habla, observando sus
características más importantes e
incluso sacar algunas conclusiones.

25. REPRESENTACIONES GRAFICAS
Veremos algunas representaciones gráficas
básicas de variables cuantitativas discretas y
continuas, variables cualitativas.
1.- Gráficos para datos cuantitativos discretos
1.1.- Diagrama de barras.
Se representa en un plano cartesiano, donde
en el eje horizontal se representan los valores
discretos que toma la variable, y sobre cada
uno de ellos se dibuja una barra vertical con
una altura igual a la frecuencia simple
correspondiente.

26. 1.2.- Diagrama de escalera
Se representa en un plano cartesiano, donde en el
eje horizontal se representan los valores discretos que
toma la variable, y sobre el eje vertical representamos
las frecuencias acumuladas, obteniéndose un gráfico
en forma de escalera.

27. 2.2.-Diagrama de sectores
Consiste en representar sobre un círculo los
diferentes atributos o modalidades teniendo en
cuenta que cada sector circular tiene un ángulo
proporcional a la correspondiente frecuencia. El
ángulo de cada sector circular se calcula
multiplicando por 360º la frecuencia relativa.

28. 3.- Gráficos para datos cuantitativos continuos
3.1.- Histograma
Es un conjunto sucesivo de rectángulos, cuya
base es igual a la amplitud de un intervalo
( amplitud constante ) y la altura es igual a la
respectiva frecuencia .
Si las longitudes de los intervalos no son
iguales, cada rectángulo tendrá una altura igual
a la densidad de frecuencia que es el cociente
entre fi y ci ,
es decir di = fi / ci i = 1,2,…,k

29. 3.2.- Polígono de frecuencias.
Es el gráfico que se forma al unir los puntos medio de
las bases superiores de los rectángulos del
histograma y cerrar el polígono cortando el eje de
abscisas, de forma que el área encerrada entre el
polígono de frecuencias y el eje horizontal coincida
con el área del histograma.
3.3.- Polígono de frecuencias acumuladas.
Sobre el eje horizontal se representan los extremos
de los intervalos y sobre el eje vertical las frecuencias
acumuladas. Para construirlo, se dibuja en el extremo
superior de cada intervalo una línea horizontal igual a
la frecuencia acumulada. La poligonal obtenida al unir
estos puntos se denomina polígono de frecuencias.

31. TRABAJO PARA PRESENTAR
Apellidos y nombres………………………..
Los siguientes datos son las tallas de
54 estudiantes elegidos al azar de un
grupo de mil estudiantes de una
determinada Facultad.
1,54 1,57 1,60 1,62 1,63 1,60 1,54 1,55
1,58 1,57 1,71 1,56 1,62 1,58 1,80 1,55
1,61 1,65 1,56 1,62 1,63 1,60 1,58 1,53
1,50 1,59 1,63 1,54 1,50 1,62 1,59 1,71
1,48 1,56 1,65 1,59 1,49 1,62 1,65 1,68
1,59 1,58 1,58 1,72 1,57 1,67 1,64 1,55
1,64 1,66 1,66 1,45 1,75 1,67

32. 1)¿Qué constituye la población?
2)¿Cuál es la variable en estudio?
3)Organice y presente los datos en una
tabla de distribución con K=7 intervalos
4)Interprete: f2 , h3 , F4 , H5
5)Halle la media e interprete.
6)Halle la mediana e interprete.
7)Halle la moda e interprete.
8)Halle la desviación estándar.
9)Indice de asimetría de Pearson.
10)Indice de apuntamiento, usando
percentiles.
Nota: Solamente responder las
preguntas numeradas.