Ejemplo de perceptrón simple con la compuerta lógica AND, y usando el modelo de aprendizaje supervisado Corrección de Error.

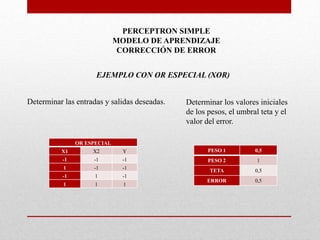
1. PERCEPTRON SIMPLE
MODELO DE APRENDIZAJE
CORRECCIÓN DE ERROR
EJEMPLO CON OR ESPECIAL (XOR)
Determinar las entradas y salidas deseadas.
OR ESPECIAL
X1 X2 Y
-1 -1 -1
1 -1 -1
-1 1 -1
1 1 1
Determinar los valores iniciales
de los pesos, el umbral teta y el
valor del error.
PESO 1 0,5
PESO 2 1
TETA 0,5
ERROR 0,5

2. Determinar la función de activación.
F(V)
1 SI V > 0
-1 SI V = < 0
De acuerdo con la regla de aprendizaje :

3. Iniciar a calcular.
Para el primer par ordenado:
1 -1 -1 -1
resultado de cálculo
-1 comparación con funcion de actuivación
-1 Ok Comparación con la respuesta deseada
El resultado realizado de acuerdo con la regla de aprendizaje es: -1, Se
realiza seguidamente la comparación con la función de activación donde nos
dice que si el valor obtenido en el cálculo de aprendizaje es mayor que cero,
entonces aproxímese a 1 y que si el valor obtenido es menor o igual que cero,
entonces aproxímese a -1. En este caso como el valor obtenido es -1, es decir
que es menor que cero, por tanto se aproximará a -1.
Finalmente comparamos esta aproximación con la salida esperada , si es igual
podemos continuar evaluando los siguientes pares ordenados, de lo contrario
de debe realizar la corrección del error.
En este caso el valor de la aproximación es -1 y es igual a la salida deseada
que es -1, por tanto procedemos a evaluar los siguientes pares ordenados.

4. Para el segundo par ordenado:
2 1 -1 -1
0
-1 Ok
Para el tercer par ordenado:
3 -1 1 -1
1
1 Recalcular
El valor que se esperaba era un -1, por consiguiente se
procede a realizar un re cálculo de pesos y volver a
evaluar. A Continuación las fórmulas necesarias para
realizar el re cálculo.

6. Recalcular el valor de los pesos y el valor de teta:
CORRECCIÓN DE ERROR
Recalcular Pesos EN PASO 3
NEW PESO 1 1,5
NEW PESO 2 1
NEW TETA -0,5
Evaluar el tercer par ordenado con los nuevos valores obtenidos:
3 -1 1 -1
-1
-1 Ok
Se obtuvo el valor deseado.

7. Evaluar todos los pares ordenados con los valores de los nuevos pesos y el
nuevo valor de teta.
4 1 1 1
2
1 Ok
1 -1 -1 -1
-3
-1 Ok
2 1 -1 -1
0
-1 Ok
Al observar que el valor de los pesos y teta, permiten que las salidas
esperadas por cada par ordenado correspondan, se dice que el
algoritmos converge con:
el valor de los pesos: 1,5 y 1.
el valor de teta: -0,5.

8. En síntesis tenemos:
PESO 1 0,5
X1 X2 Y PESO 2 1
1 -1 -1 -1 TETA 0,5
2 1 -1 -1 ERROR 0,5
3 -1 1 -1
4 1 1 1
1 -1 -1 -1
com-p1aración con funcion de actuivación
Cálculo -1 Ok Comparación con la respuesta deseada
2 1 -1 -1
0
-1 Ok
3 -1 1 -1
1
1 Recalcular
CORRECCIÓN DE ERROR
NEW PESO 1 1,5
NEW PESO 2 1
NEW TETA -0,5
3 -1 1 -1
-1
-1 Ok
4 1 1 1
2
1 Ok
1 -1 -1 -1
-3
-1 Ok
2 1 -1 -1
0
-1 Ok
Recalcular Pesos EN PASO 3
FUNCIÓN DE ACTIVACIÓN
RECALCULANDO CON LOS NUEVOS PESOS
F(V)
OR ESPECIAL
1 SI V >
/ -1 SI V = <
0