Para rezagado 1

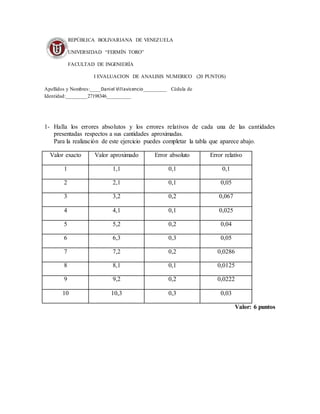
1. REPÚBLICA BOLIVARIANA DE VENEZUELA
UNIVERSIDAD “FERMÍN TORO”
FACULTAD DE INGENIERÍA
I EVALUACION DE ANALISIS NUMERICO (20 PUNTOS)
Apellidos y Nombres:____Daniel Villavicencio_________ Cédula de
Identidad:________27198346_________
1- Halla los errores absolutos y los errores relativos de cada una de las cantidades
presentadas respectos a sus cantidades aproximadas.
Para la realización de este ejercicio puedes completar la tabla que aparece abajo.
Valor exacto Valor aproximado Error absoluto Error relativo
1 1,1 0,1 0,1
2 2,1 0,1 0,05
3 3,2 0,2 0,067
4 4,1 0,1 0,025
5 5,2 0,2 0,04
6 6,3 0,3 0,05
7 7,2 0,2 0,0286
8 8,1 0,1 0,0125
9 9,2 0,2 0,0222
10 10,3 0,3 0,03
Valor: 6 puntos

2. 2. Usando el método de punto fijo vamos a aproximar la solución de la ecuación
dentro del intervalo .
𝑝 = 𝑓( 𝑝) → 𝑝 = 𝑝3
+ 4𝑝2
− 10 → 𝑝3
+ 4𝑝2
− 𝑝 − 10 = 0
Al factorizar se consigue que las raíces de este polinomio son
𝑝1 = −2, 𝑝2 = 1,45; 𝑝3 = −3,45
En este caso la solución que está dentro del intervalo es p=1,45
𝑓( 𝑥) = 𝑥3
+ 4𝑥2
− 10
𝑓′( 𝑥) = 3𝑥2
+ 8𝑥
𝑝 𝑘 = 𝑝 𝑘−1
3
+ 4𝑝 𝑘−1
2
− 10
Entonces iniciamos el proceso de iteración con p0=1,40
𝑝1 = 𝑝0
3
+ 4𝑝0
2
− 10 = 0,584
𝑝2 = 𝑝1
3
+ 4𝑝1
2
− 10 = −8,44

3. 𝑝3 = 𝑝2
3
+ 4𝑝2
2
− 10 = −326,28
𝑝4 = 𝑝3
3
+ 4𝑝3
2
− 10 = −34309499,98
Entonces se observa que
lim
𝑘→∞
𝑝 𝑘 = −∞
Por lo que la solución no converge a 1,45.
3. Usar el método de Newton-Raphson para aproximar la raíz de ,
comenzando con y hasta que .
La fórmula de iteración para el método de Newton es
𝑥 𝑘 = 𝑥 𝑘−1 −
𝑓(𝑥 𝑘−1)
𝑓′(𝑥 𝑘−1)
En este caso se tiene que
𝑓( 𝑥) = 𝑥 − 1 + 𝑡𝑎𝑛−1
𝑥
Se calcula la derivada de f(x):
1arctan)(  xxxf
00 x %1a

4. 𝑓′( 𝑥) = 1 +
1
1 + 𝑥2
=
2 + 𝑥2
1 + 𝑥2
Se evalúan la función f(x) y su primera derivada en xk-1:
𝑓( 𝑥 𝑘−1) = 𝑥 𝑘−1 − 1 + 𝑡𝑎𝑛−1( 𝑥 𝑘−1)
𝑓′( 𝑥 𝑘−1) =
2 + 𝑥 𝑘−1
2
1 + 𝑥 𝑘−1
2
Se sustituyen ahora en la ecuación iterativa de Newton-Raphson:
𝑥 𝑘 = 𝑥 𝑘−1 −
𝑥 𝑘−1 − 1 + 𝑡𝑎𝑛−1( 𝑥 𝑘−1)
2 + 𝑥 𝑘−1
2
1 + 𝑥 𝑘−1
2
𝑥 𝑘 = 𝑥 𝑘−1 −
(1 + 𝑥 𝑘−1
2 )(𝑥 𝑘−1 − 1 + 𝑡𝑎𝑛−1( 𝑥 𝑘−1))
2 + 𝑥 𝑘−1
2

5. El erro absoluto se calcula de acuerdo con la expresión:
𝐸 𝑎 = | 𝑥 − 𝑥̂|
En donde x es el valor exacto y 𝑥̂ es el valor aproximado
En este caso no indican el valor exacto x pero sabemos que
𝑓( 𝑥) = 𝑥 − 1 + 𝑡𝑎𝑛−1
𝑥
Y como se sabe que el valor exacto de x se encuentra para f(x)=0, entonces
𝑥 − 1 + 𝑡𝑎𝑛−1
𝑥 = 0
Resolviendo se encuentra que
𝑥 = tan(1 − 𝑥)
La solución exacta de esta ecuación ocurre en x=0,52.
Comenzamos el proceso iterativo en k=1:
Se inicia con x0=0 y el error absoluto |Ea|<0,01

6. 𝑥1 = 𝑥1−1 −
(1 + 𝑥1−1
2 )(𝑥1−1 − 1 + 𝑡𝑎𝑛−1( 𝑥1−1))
2 + 𝑥1−1
2
𝑥1 = 𝑥0 −
(1 + 𝑥0
2)(𝑥0 − 1 + 𝑡𝑎𝑛−1( 𝑥0))
2 + 𝑥0
2
𝑥1 = 0,5
𝐸 𝑎 = |0,52 − 0,5| = 0,02 > 0,01
Se debe continuar con el proceso iterativo.
k=2:
𝑥2 = 𝑥1 −
(1 + 𝑥1
2)(𝑥1 − 1 + 𝑡𝑎𝑛−1( 𝑥1))
2 + 𝑥1
2
𝑥2 = 0,512
𝐸 𝑎 = |0,52 − 0,512| = 0,008 < 0,01
Como el error absoluto calculado en este paso es menor del 1%, entonces la solución
aproximada para la ecuación
𝑓( 𝑥) = 𝑥 − 1 + 𝑡𝑎𝑛−1
𝑥
es x=0,512