Pearson Ana
•Descargar como PPT, PDF•
0 recomendaciones•638 vistas
Denunciar
Compartir
Denunciar
Compartir
Recomendados
Recomendados
Más contenido relacionado
La actualidad más candente
La actualidad más candente (20)
Capítulo 06, Distribuciones discretas de probabilidad

Capítulo 06, Distribuciones discretas de probabilidad
Estimación.intervalos de confianza para la media y para las proporciones

Estimación.intervalos de confianza para la media y para las proporciones
Destacado
Destacado (20)
Examen de certificacion de ADWORDS: C10: Cómo gestionar varias cuentas

Examen de certificacion de ADWORDS: C10: Cómo gestionar varias cuentas
Similar a Pearson Ana
Similar a Pearson Ana (20)
Más de gueste74d15
Más de gueste74d15 (16)
Pearson Ana
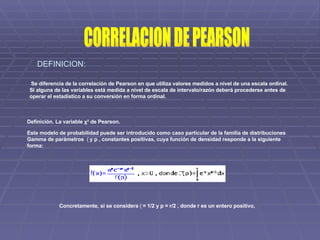
- 1. CORRELACION DE PEARSON Se diferencia de la correlación de Pearson en que utiliza valores medidos a nivel de una escala ordinal. Si alguna de las variables está medida a nivel de escala de intervalo/razón deberá procederse antes de operar el estadístico a su conversión en forma ordinal. Definición. La variable χ 2 de Pearson. Este modelo de probabilidad puede ser introducido como caso particular de la familia de distribuciones Gamma de parámetros y p , constantes positivas, cuya función de densidad responde a la siguiente forma: DEFINICION: Concretamente, si se considera = 1/2 y p = r/2 , donde r es un entero positivo,
- 2. el modelo de probabilidad resultante se denomina χ2, Chi-cuadrado, con r grados de libertad. Gráfica de la función de densidad de la variable χ2 con 10 grados de libertad: Resultado que afecta a la distribución de S2. Si X1, X2,..., Xn son variables aleatorias independientes con ley de probabilidad normal N(μ,σ) , es decir, una muestra aleatoria de tamaño n extraída de una población N(μ,σ), entonces Sigue la ley de probabilidad del modelo χ2 con (n-1) grados de libertad.
- 3. Algunas preguntas de importancia en el diseño esta- dístico del análisis de correlación de un estudio son: ¿Las variables con cuantitativas o cualitativas?, ¿la distribución de los datos obtenidos es paramétrica o no paramétrica? (normal, binomial, hipergeométrica, ji cuadrada, etc.), ¿el tamaño de la muestra es suficiente para adecuarse al modelo estadístico?, ¿la muestra estudiada fue aleatoria o no aleatoria?, ¿las mediciones son independientes o pareadas?, ¿cuántos grupos se estudiaron uno, dos tres o más?, ¿cuál es el propósito de la investigación, describir, comparar, correlacionar, predecir? Las respuestas adecuadas a estas preguntas prácticamente definen el diseño estadístico. IMPORTANCIA