Presentacion t student
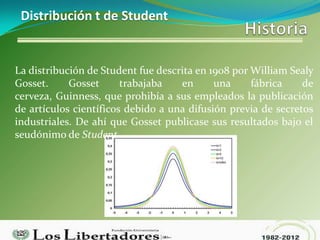
- 1. Distribución t de Student La distribución de Student fue descrita en 1908 por William Sealy Gosset. Gosset trabajaba en una fábrica de cerveza, Guinness, que prohibía a sus empleados la publicación de artículos científicos debido a una difusión previa de secretos industriales. De ahí que Gosset publicase sus resultados bajo el seudónimo de Student.
- 2. Distribución t de Student William Sealy Gosset (11 de junio de 1876– 16 de octubre de 1937) fue un estadístico, mejor conocido por su sobrenombre literario Student. Nacido en Canterbury, hijo de Agnes Sealy Vidal y el coronel Frederic Gosset, asistió a la famosa escuela privada Winchester College, antes de estudiar química y matemática en el New College de Oxford. Tras graduarse en 1899, se incorporó a las destilerías Guinness en Dublín.
- 3. Distribución t de Student o Tras graduarse en 1899, se incorporó a las destilerías Guinness en Dublín. (negocio agroquímico progresista) o Aplico sus conocimientos estadísticos tanto a la destilería como a la granja (para seleccionar las mejores variedades de cebada) o Guinness prohibió a sus empleados la publicación de artículos independientemente de la información que contuviesen
- 4. Distribución t de Student o De ahí el uso de su pseudónimo Student en sus publicaciones, para evitar que su empleador lo detectara, o su logro más famoso se conoce ahora como la distribución t de Student o Gosset publicó El error probable de una media
- 5. Distribución t de Student R.A. Fisher quien apreció la importancia de los trabajos de Gosset sobre muestras pequeñas, tras recibir correspondencia de Gosset en la que le decía le envío una copia de las Tablas de Student, ¡ya que es la única persona que probablemente las use jamás! La estadística de Gosset era z = t/√(n - 1). Fisher introdujo la forma t debido a que se ajustaba a su teoría de grados de libertad Fisher es responsable también de la aplicación de la distribución t a la regresión.
- 6. Distribución t de Student En 1935 dejó Dublín para ocupar el puesto de Destilador Jefe (Head Brewer), a cargo de la parte científica de la producción, en la nueva destilería Guinness de Londres. Murió en Beaconsfield, Inglaterra. Gosset fue un hombre modesto que cortó a un admirador con el comentario "Fisher lo hubiera descubierto de todas maneras".
- 7. Distribución t de Student En probabilidad y estadística la distribución t de student es una distribución de probabilidad que surge del problema de estimar la media de una población normalmente distribuida cuando el tamaño de la muestra es pequeña
- 8. Distribución t de Student Se utiliza para hacer estimaciones de parámetros de las poblaciones a partir de los valores de los estadísticos correspondientes en las muestras, cuando se desconoce el valor de la varianza o la desviación estándar de la población.
- 9. Distribución t de Student o 1. cada curva t tiene forma de campana con centro en 0. o Cada curva t, es mas dispersa que la curva normal estándar. o A medida de que aumenta, la dispersión de la curva t correspondiente disminuye. o a medida de que k tiende a infinito, la secuencia de curvas t se aproxima a la curva normal estándar.
- 10. Distribución t de Student Las observaciones proceden de una población que tiene distribución normal con media y desviación estándar. En la practica a no ser que la muestra sea muy pequeña, es suficiente con que la población sea simétrica y con un solo pico. Tanto la media como la desviación típica son parámetros desconocidos.
- 11. Distribución t de Student Cuando la desviación estándar del estadístico se estima a partir de datos, el resultado se llama error estándar del estadístico. El error estándar se calcula usando la formula:
- 12. Distribución t de Student o Cuando conocemos el valor de la desviación estándar , basamos los intervalos de confianza y las pruebas para la media ene le estadístico z de una muestra. o T= media muestra-media/ desviación estándar/ raíz n
- 13. Distribución t de Student o Representan el número de datos independientes que se pueden tomar de la población para construir la muestra, de tal manera que los valores de los estadísticos en la muestra sean cercanos a los valores de los parámetros correspondientes en la población. o Al escoger una muestra de tamaño n, el numero de datos independientes que se pueden tomar es n-1, ya que el ultimo dato que se escoja, es el que viene a definir el valor del estadístico en la muestra gl=n-1
- 14. Distribución t de Student
- 15. Distribución t de Student
- 16. Distribución t de Student
- 17. Distribución t de Student Comparación de Tipo de Curvas
- 18. Distribución t de Student Comportamiento de la distribución T comparada con la distribución Z Representación Grafica
- 19. Distribución t de Student Donde el parámetro n de tn , se denomina grados de libertad de la distribución. La distribución t de Student existe para todos los valor es de x reales, y es simétrica respecto al eje y.
- 20. Distribución t de Student Para distintos valores de n y de x se puede buscar su probabilidad acumulada p
- 21. Distribución t de Student Hipótesis de dos lados Hacia el lado derecho
- 22. Distribución t de Student Hacia el izquierdo
- 23. Distribución t de Student En esta tabla hay dos entradas, en la fila superior están los valores de n para los que se ha calculado la probabilidad, en la columna de la izquierda los de x, para x igual o mayor que cero, en incrementos de 0,05, para cada valor de n y de la x correspondiente tenemos la probabilidad acumulada, expresada con tres cifras decimales.
- 24. Distribución t de Student n p 0,50 0,55 0,60 0,70 0,75 0,80 0,85 0,90 0,95 1 0,324 919 0,726 543 1,000 001 1,376 382 1,962 612 3,077 685 6,313 749 31,820 96 63,655 90 2 0,288 675 0,617 214 0,816 497 1,060 660 1,386 206 1,885 619 2,919 987 6,964 547 9,924 988 3 0,276 671 0,584 390 0,764 892 0,978 472 1,249 778 1,637 745 2,353 363 4,540 707 5,840 848 4 0,270 722 0,568 649 0,740 697 0,940 964 1,189 567 1,533 206 2,131 846 3,746 936 4,604 080 5 0,267 181 0,559 430 0,726 687 0,919 543 1,155 768 1,475 885 2,015 049 3,364 930 4,032 117 6 0,264 835 0,553 381 0,717 558 0,905 703 1,134 157 1,439 755 1,943 181 3,142 668 3,707 428 7 0,263 167 0,549 110 0,711 142 0,896 030 1,119 159 1,414 924 1,894 578 2,997 949 3,499 481 8 0,261 921 0,545 934 0,706 386 0,888 890 1,108 145 1,396 816 1,859 548 2,896 468 3,355 381 9 0,260 956 0,543 480 0,702 722 0,883 404 1,099 716 1,383 029 1,833 114 2,821 434 3,249 843 10 0,260 185 0,541 528 0,699 812 0,879 057 1,093 058 1,372 184 1,812 462 2,763 772 3,169 262 11 0,259 556 0,539 937 0,697 445 0,875 530 1,087 667 1,363 430 1,795 884 2,718 079 3,105 815 12 0,259 033 0,538 618 0,695 483 0,872 609 1,083 212 1,356 218 1,782 287 2,680 990 3,054 538 13 0,258 591 0,537 504 0,693 830 0,870 151 1,079 469 1,350 172 1,770 932 2,650 304 3,012 283 14 0,258 212 0,536 552 0,692 417 0,868 055 1,076 280 1,345 031 1,761 309 2,624 492 2,976 849 15 0,257 885 0,535 729 0,691 197 0,866 245 1,073 531 1,340 605 1,753 051 2,602 483 2,946 726
- 25. Distribución t de Student
- 26. Distribución t de Student 1 La longitud de los tornillos fabricados en una fábrica tienen media μ=10 mm y desviación s=1 mm, calcular la probabilidad de que en una muestra de tamaño n=25, la longitud media del tornillo sea inferior a 20.5 mm: P (μ<20.5) Estandarizamos T=(X-μ)/(s/√n) que sigue una distribución t de n-1 grados de libertad T=(20.5-20)/(1/√25) = 2.5 P (μ<20.5) --> P (T<2.5) ~ t(24) P (T<2.5) = 0.9902 P (μ<20.5)=0.9902 La probabilidad que la longitud media de la muestra de 25 tornillos sea inferior a 20.5 mm es del 99.02%
- 27. Distribución t de Student 2. Se desea obtener un intervalo de confianza al 99% para el de confianza al 99% para el tiempo medio requerido para tiempo medio requerido para realizar un trabajo. Realizar un trabajo. t= Una confianza del 99% con(n-1) grados de libertad.(n-1) grados de libertad.
- 28. Distribución t de Student 3. Una muestra aleatoria de 16Una muestra aleatoria de 16mediciones produce una media mediciones produce una media y una desviación estándar de 13y una desviación estándar de 13 y 5.6 minutos respectivamente y 5.6 minutos respectivamente GL=16-1=GL=16-1= 1515 99 % ά2=.005ά1=.005ά= 1%ά= .01ά/2=.005 n= 16 X=13 minutosX=13 minutos S= 5.6 minutos S= 5.6 minutos t=2.947t=2.947∂∂=13=13±2.947(5.6/√16)±2.947(5.6/√16)∂∂=13=13±4.12±4.12∂∂1=17.1 2 minutos1=17.12 minutos∂∂2=8.88 minutos2=8.88 minutos x=xx=x± t± ts .s .√√nn
- 29. Distribución t de Student X=13 minutos=13 minutos S= 5.6 minutos= 5.6 minutos t=2.947t=2.947∂∂=13=13±2.947(5.6/√16)±2.947(5.6/√16)∂∂=13=13±4.12±4.12∂∂1=17.12 minutos1=17.12 minutos∂∂2=8.88 minutos2=8.88 minutos x=xx=x± t± ts .s .√√nn Tiempo medio requerido para realizar el trabajo será entre 8.88 y 17.12minutos con un n= 16 X=13 minutos=13 minutos S= 5.6 minutos= 5.6 minutos t=2.947t=2.947∂∂=13=13±2.947(5.6/√16)±2.947(5.6/√16)∂∂=13=13±4.12±4.12∂∂1=17.12 minutos1=17.12 minutos∂∂2=8.88 minutos2=8.88 minutos x=xx=x± t± ts .s .√√nn Tiempo medio requerido para realizar el trabajo será entre 8.88 y 17.12minutos con un
- 30. Distribución t de Student