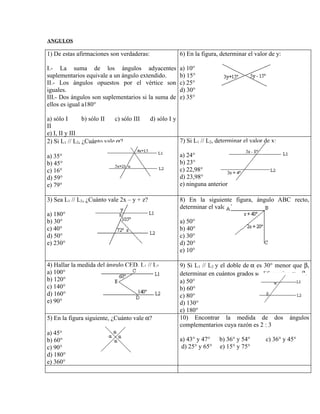
1. ANGULOS
1) De estas afirmaciones son verdaderas: 6) En la figura, determinar el valor de y:
I.- La suma de los ángulos adyacentes a) 10°
suplementarios equivale a un ángulo extendido. b) 15°
II.- Los ángulos opuestos por el vértice son c) 25°
iguales. d) 30°
III.- Dos ángulos son suplementarios si la suma de e) 35°
ellos es igual a180°
a) sólo I b) sólo II c) sólo III d) sólo I y
II
e) I, II y III
2) Si L1 // L2, ¿Cuánto vale α? 7) Si L1 // L2, determinar el valor de x:
a) 35° a) 24°
b) 45° b) 23°
c) 16° c) 22,98°
d) 59° d) 23,98°
e) 79° e) ninguna anterior
3) Sea L1 // L2, ¿Cuánto vale 2x – y + z? 8) En la siguiente figura, ángulo ABC recto,
determinar el valor de x:
a) 180°
b) 30° a) 50°
c) 40° b) 40°
d) 50° c) 30°
e) 230° d) 20°
e) 10°
4) Hallar la medida del ángulo CED. L1 // L2 9) Si L1 // L2 y el doble de α es 30° menor que β,
a) 100° determinar en cuántos grados se diferencian α y β.
b) 120° a) 50°
c) 140° b) 60°
d) 160° c) 80°
e) 90° d) 130°
e) 180°
5) En la figura siguiente, ¿Cuánto vale α? 10) Encontrar la medida de dos ángulos
complementarios cuya razón es 2 : 3
a) 45°
b) 60° a) 43° y 47° b) 36° y 54° c) 36° y 45°
c) 90° d) 25° y 65° e) 15° y 75°
d) 180°
e) 360°

2. 11) En la figura siguiente, ¿Cuánto vale x? 15) En la siguiente figura, determinar el valor de x:
a) 180° – ( a + b) a) 30°
b) 180° – a + b b) 45°
c) 180° + a + b c) 60°
d) 180° + ( a – b) d) 65°
e) 180° – ( a – b) e) 90°
12) Hallar la medida del ángulo que, disminuido en 16) Si el 25% de α es 5,5° y el 40% de β es 52°,
su suplemento, es igual al triple de su calcular α +β
complemento:
a) 22° b) 40° c) 92° d) 130°
a) 22,5° b) 45° c) 60° d) 90° e) 180° e) 152°
13) Sean L1 // L2 y α : β = 2 : 5. Determinar el 17) Si α = 38° y β = 24°, encontrar el valor de x e
valor de α. y.
a) 20° a) x = 117°; y = 25°
b) 40° b) x = 118°; y = 24°
c) 50° c) x = 116°; y = 23°
d) 120° d) x = 23°; y = 116°
e) 100° e) x = 24°; y = 118°
14) Si L1 // L2 y L secante, determinar el valor de 18) Si L1 // L2, L4 es bisectriz de α y γ = 35°,
x: ¿Cuánto mide el suplemento de β?
a) 2° a) 70°
b) 3° b) 180°
c) 4° c) 90°
d) 27° d) 35°
0
 150  e) 110°
e)  
 11 