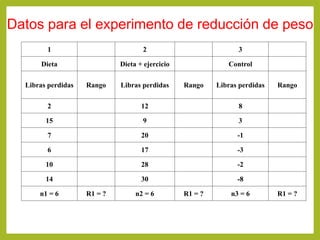
Este documento describe la prueba de Kruskal-Wallis, una prueba no paramétrica que se usa como sustituto del ANOVA cuando los supuestos de normalidad y homogeneidad de varianza no se cumplen. Se aplica a diseños con más de dos grupos independientes y evalúa si las sumas de los rangos de los grupos difieren de manera significativa. El documento incluye un ejemplo de aplicación de la prueba de Kruskal-Wallis a un experimento de reducción de peso con tres grupos.

1. LA PRUEBA DE
KRUSKALWALLIS

2. PRUEBA KRUSKAL - WALLIS
• Es una prueba no paramétrica
• Trabaja con un diseño para grupos independientes que emplea k
numero de muestras.
• Método que se usa como sustituto para el ANOVA paramétrico,
cuando los supuestos de ANOVA son seriamente violados.
• No supone normalidad en la población ni homogeneidad de
varianza
• Se requiere de una escala ordinal
• Sigue la distribución chi cuadrado
)1(3
)1(
12
1
2


 

N
n
R
NN
H
K
i i
i

3. ¿HAY NORMALIDAD?
SI NO
2 muestras
U MannWhitney
> 2 muestras
Kruskal-Wallis
> 2 muestras
ANOVA2 muestras
t-student

4. PRUEBA KRUSKAL - WALLIS
Ejemplo:
• Una psicóloga de la salud, contratada por una gran corporación, está interesada
en evaluar dos programas de reducción de peso que considera aplicar con los
empleados de su corporación. Conduce un experimento en el cual 18 empleados
obesos son asignados al azar a tres condiciones, con seis sujetos cada una. Los
sujetos en la condición 1 se someten a una dieta que reduce su ingesta calórica
diaria en 500 calorías. Los sujetos en la condición 2 reciben la misma dieta
restringida, pero, además, se les pide caminar dos kilómetros cada día. La
condición tres es la condición control, en la cual se pide a los sujetos que
mantengan su consumo y los hábitos de ejercicio acostumbrados.
• Nota: Un numero positivo indica pérdida de peso y un número negativo indica
aumento de peso.
• Respetando los supuestos.
a) ¿ Cuál es la hipótesis alternativa?
b) ¿ Cuál es la hipótesis nula?
c) ¿ Cuál es su conclusión? Utilice α = 0.05

5. Datos para el experimento de reducción de peso
1 2 3
Dieta Dieta + ejercicio Control
Libras perdidas Rango Libras perdidas Rango Libras perdidas Rango
2 12 8
15 9 3
7 20 -1
6 17 -3
10 28 -2
14 30 -8
n1 = 6 R1 = ? n2 = 6 R1 = ? n3 = 6 R1 = ?

6. SOLUCION:
Ho: μ1=μ2=μ3
Ha : Cuando menos una de las distribuciones de la población es diferente
Calcular el estadístico apropiado
• Todos los puntaje se agrupan y se ordenan por rangos, en los cuales se asigna
1 al puntaje más bajo, 2 al siguiente y N al más alto.
• Se suman los rangos.
• Las sumas de los rangos se representan como R1, R2, R3.
• La prueba de kruskal-Wallis evalúa si estas sumas de rangos difieren una de
otra tanto que resulte no razonable considerar que provienen de muestras que
fueron seleccionados al azar de la misma población
)1(3
)1(
12
1
2


 

N
n
R
NN
H
K
i i
i

7. SOLUCION:
• K = número de muestras o grupos
• ni = número de puntaje en la muestra i
• n1 = número de puntaje en la muestra 1
• n2 = número de puntaje en la muestra 2
• n3 = número de puntaje en la muestra 3
• nk = número de puntaje en la muestra k
• N = número de puntaje en todas las muestras combinadas
• Ri = Suma de los rangos para la muestra i
• R1 = Suma de los rangos para la muestra 1
• R2 = Suma de los rangos para la muestra 2
• R3 = Suma de los rangos para la muestra 3
• Rk = Suma de los rangos para la muestra ik
)1(3
)1(
12
1
2


 

N
n
R
NN
H
K
i i
i

8. SOLUCION:
Evaluar el estadístico
• Si el número de puntaje en cada muestra es cinco o más, la distribución de
muestreo del estadístico H es aproximadamente el mismo que chi2 con gl=k-1. E n
el presente experimento, gl = k-1= 3-1= 2. De la tabla H con alfa = 0.05 y gl=2 Hcrit
= 5.991
Regla de decisión:
Si Hobt >= Hcrit, rechazar Ho
Si Hobt<= Hcrit, no rechazar Ho
Conclusión:
Dado que Hobt< 5.991, rechazamos Ho Tal parece que las condiciones
no son iguales respecto de la perdida de peso.

9. PRUEBA KRUSKAL - WALLIS
Ejemplo:
• Un investigador del sueño conduce un experimento para determinar si la pérdida
de sueño afecta la capacidad de mantener la atención sostenida . Quince
individuos son divididos al azar en los siguientes tres grupos de cinco sujetos
cada uno: grupo 1, el cual duerme la cantidad normal de sueño (de 7 a 8 horas);
el grupo 2, el cual es privado del sueño durante 24 horas; y el grupo 3, el cual es
privado del sueño durante 48 horas. Los tres grupos se someten a la misma
prueba con tareas de vigilancia auditiva . A los sujetos se les presentan tonos de
medio segundo espaciados a intervalos regulares durante una hora. En
ocasiones, uno de los tonos es un poco más breve que los restantes. La tarea de
los sujetos es detectar los tonos breves. Se observaron los siguientes porcentajes
de detecciones correctas.
• Respetando los supuestos analice los datos.
a) ¿ Cuál es la hipótesis alternativa?
b) ¿ Cuál es la hipótesis nula?
c) ¿ Cuál es su conclusión? Utilice α = 0.05

10. Sueño
normal
Privación del sueño
durante 24 horas
Privación del
sueño durante 48
horas
Rango Rango Rango
85 60 60
83 58 48
76 76 38
64 52 47
75 63 50
n1 = R1 = ? n2 = R1 = ? n3 = R1 = ?